Statistik - Die Grundlagen
Der folgende Abschnitt beschäftigt sich noch einmal mit den Grundlagen der Statistik. Im Verlaufe der nächsten Kapitel wird relativ grundlegend noch einmal der Ganze Unterbau der Statistik entwickelt. Dabei wird so weit wie möglich auf komplizierte mathematische Grundlagen verzichtet. Allerdings, ganz ohne Mathematik geht es leider nicht, sollte sich aber vom Anspruch nicht über die 10. Schulklasse hinaus bewegen.
Die erste Frage die sich bei der Anwendung von statistischen Verfahren stellt ist: Wofür wird die Statistik überhaupt benötigt?
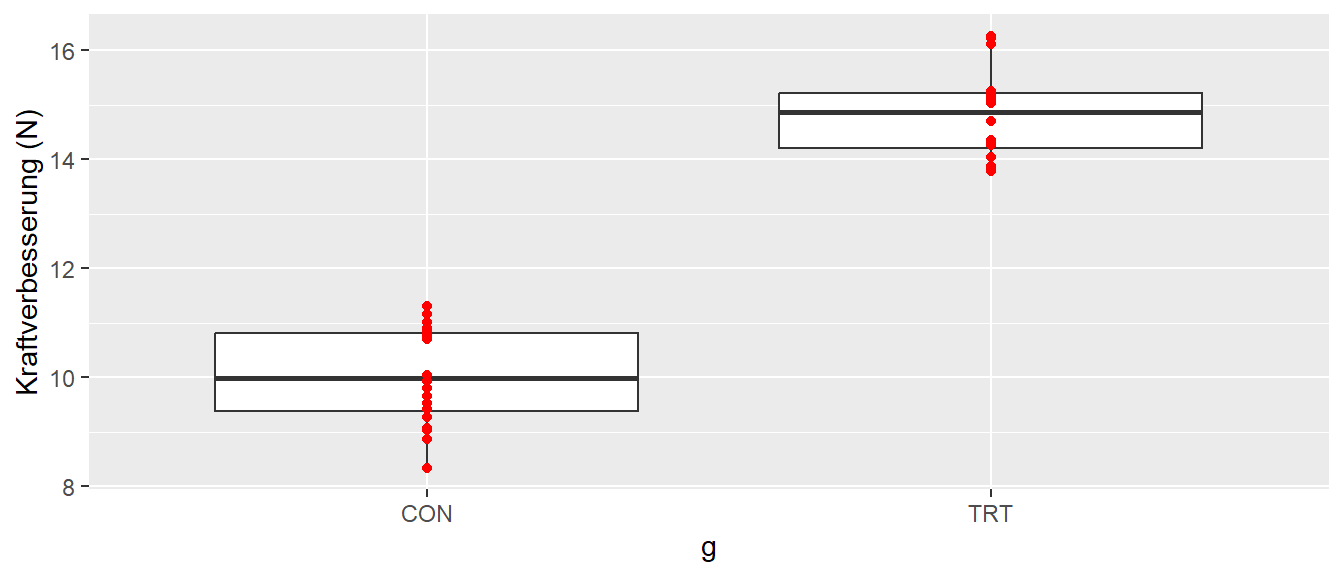
Dazu sei zunächst mit einem einfachen Beispiel begonnen. Ausgehend von einer relevanten Forschungsfragestellung wurde ein einfacher Datensatz gesammelt. Der Datensatz enthält Informationen über zwei unterschiedliche Gruppen die miteinander verglichen werden sollen. Die eine Gruppe wird der Einfachheit halber als Treatmentgruppe (TRT) bezeichnet und hat beispielsweise ein spezielles Krafttraining durchgeführt, während die andere Gruppe eine Kontrollgruppe (CON) darstellt, die beispielsweise ein übliches, traditionelles Krafttraining durchgeführt hat. Beide Gruppen sind gleich groß gewesen, d.h. die Anzahl an Versuchspersonen sind in beiden Gruppen gleich mit jeweils \(N = 20\) Personen. Wo die Teilnehmerinnen und Teilnehmer herkommen, sei zunächst vernachlässigt, die Personen sind aber zufällig in die beiden Gruppen eingeteilt worden. Der Fakt, dass die Gruppen zufällig in die Gruppen eingeteilt wurden, die Gruppenzugehörigkeit randomisiert wurde, führt dazu, dass davon ausgegangen werden kann, dass kein Unterschied zwischen den beiden Gruppen vor Beginn des Trainings bestehen sollte. Es wurde nach der Trainingsperiode das folgende Ergebnis erhalten (siehe Abbildung 1).

In Abbildung 1 sind die Daten mittels eines Boxplots zusammen mit den Rohdaten als rote Punkte dargestellt. Die abhängige Variable ist die Verbesserung in der Kraftfähigkeit in \(N\). Die Daten zeigen eigentlich relativ deutlich, dass die Verbesserung in der Treatmentgruppe deutlich höher ausgefallen ist, als diejenige in der Kontrollgruppe. Eine Darstellung in Form einer Tabelle kommt erwartungsgemäß zu der gleichen Interpretation der Daten (siehe Tabelle 1).
| Gruppe | \(\bar{F}\) | SD |
|---|---|---|
| CON | 10.05 | 0.89 |
| TRT | 14.83 | 0.78 |
Der Mittelwert in der Treatmentgruppe ist deutlich großer als derjenige in der Kontrollgruppe. Vor dem Hintergrund der Streuung der Daten ausgedrückt durch die Standardabweichung erscheint der Unterschied zwischen den beiden Gruppen bedeutsam. Wenn eine sogenannten Effektstärke berechnet werden würde, dann würde die Effektstärke als sehr groß eingestuft worden. Warum ist es nicht ausreichend das Offensichtliche zu dokumentieren, dass der Unterschied zwischen den Gruppen bei \(\Delta = 4.8\)N liegt und das Treatment somit effektiver war? Warum ist eine statistische Analyse der Daten überhaupt notwendig?
Die Antwort auf diese Frage wird in den folgenden Abschnitt erarbeitet. Im Zuge dessen werden die notwendigen Werkzeuge entwickelt um die verschiedenen notwendigen Schritte, die einer statistischen Analyse von Daten zugrundeliegend, zu verstehen und anwenden zu können. Letztendlich wird auch erarbeitet welche Art der Evidenz mittels statistischer Analysen überhaupt ermittelt werden kann. Auf das Sätze wie: “Da \(p < 0.05\) beobachtet wurde, konnte in der Studie bewiesen werden, dass …” zukünftig nicht mehr geschrieben werden.