| \(n_1\) | \(n_2\) | \(\sigma^2(D)\) | \(\sigma_e(D)\) | Effizienz |
|---|---|---|---|---|
| 1 | 11 | 1.09 | 1.04 | 0.31 |
| 2 | 10 | 0.60 | 0.77 | 0.56 |
| 3 | 9 | 0.44 | 0.67 | 0.75 |
| 4 | 8 | 0.38 | 0.61 | 0.89 |
| 5 | 7 | 0.34 | 0.59 | 0.97 |
| 6 | 6 | 0.33 | 0.58 | 1.00 |
| 7 | 5 | 0.34 | 0.59 | 0.97 |
| 8 | 4 | 0.38 | 0.61 | 0.89 |
| 9 | 3 | 0.44 | 0.67 | 0.75 |
| 10 | 2 | 0.60 | 0.77 | 0.56 |
| 11 | 1 | 1.09 | 1.04 | 0.31 |
23 Einführung
Im Folgenden beschäftigen wir uns mit experimentellen Design. D.h. wir untersuchen wie wir ein Experiment aus statistischer Sicht erstellen sollten um die Wahrscheinlichkeit einen bestimmten Effekt zu beobachten möglichst Effizient zu erhöhen. Eine zentrale Größe wird dabei immer wieder der Standardfehler \(\sigma_e\) der jeweiligen Statistik spielen die wählen um einen bestimmten Effekt zu untersuchen. Daher fangen wir erst einmal mit einem einfachen Beispiel an.
23.1 Zuteilung der Stichprobengrößen in zwei Gruppen
Die folgenden Beispiele sind alle aus Goos und Jones (2011) entnommen. Wir möchten Mittelwertsunterschied zwischen zwei Gruppen, Gruppe \(1\) und Gruppe \(2\), untersuchen. In Gruppe \(1\) haben wir eine Stichprobengröße von \(n_1\) und entsprechend eine Stichprobegröße \(n_2\) in Gruppe \(2\).
Um den Unterschied zwischen den beiden Gruppenmittelwerten zu berechnen, verwenden wir den unspektakulär:
\[\begin{equation} D = \bar{X}_1 - \bar{X}_2 \end{equation}\]
Der Unterschied \(D\) für sich ist noch relativ wenig informativ, da er mit den Einheiten und vor allem vor dem Hintergrund der Streuung der Werte zu betrachten ist. D.h. wir benötigen auch ein Maß um die Unsicherheit \(\widehat{=}\) Streuung um einen gegebenen Unterschied zu bewerten. Den Standardfehler können wir mit den uns bekannten Rechenregeln für die Varianz relativ einfach herleiten und erhalten:
\[\begin{equation} \sigma^2(D) = \frac{\sigma_1^2}{n_1} + \frac{\sigma_2^2}{n_2} \end{equation}\]
Um die Wahrscheinlichkeit zu erhöhen einen relevanten Unterschied \(D\) zwischen den Gruppen zu finden wählen wir nun ein Design des Experiments, dass die Varianz \(\sigma^2(D)\) bzw. den Standardfehler \(\sigma_e(D)\) von \(D\) möglichst klein werden lässt. Denn, umso kleiner der Standardfehler umso geringer sind die Streuungen der Stichprobenverteilung und umso geringer unsere Unsicherheit.
Schauen wir uns an, was dies in einem konkreten Fall bedeutet. Gehen wir, der Übersichtlichkeit halber, von einer Gesamtstichprobengröße \(N = 12\) aus mit Standardabweichungen in beiden Population von \(\sigma^2_1 = \sigma^2_2 = \sigma^2 = 1\). D.h. wir nehmen an, dass in beiden Stichproben die gleiche Streuung vorliegt.
In Tabelle 23.1 sind die Varianz \(\sigma^2(D)\) und der Standardfehler \(\sigma_e(D)\) gegen die Stichprobenverteilung abgetragen. Wir können sehen, dass bei gleicher Stichprobenanzahl in beiden Gruppen die Varianz und somit auch der Standardfehler den kleinsten Wert annehmen. In der fünften Spalte von Tabelle 23.1 ist ein Wert Effizient eingetragen. Dieser Wert berechnet sich aus dem Verhältnis der kleinstmöglichen Varianz zur jeweiligen Varianz. Wir können an diesem Wert abschätzen, das ein Design bei dem in einer der Gruppen nur eine einzige Person ist, die Effizienz nur noch ein Drittel dessen ist, was bei einer gleichmäßigen Stichprobenverteilung zu errreichen ist. D.h. so weit ist die übliche Herangehensweise, beide Gruppen möglichst gleichgroß zu gestalten vollkommmen sinnvoll.
Schauen wir uns als Nächstes an, wie das aussieht wenn die Stichprobengröße \(N\) anwächst. In Abbildung 23.1 ist der Standardfehler \(\sigma_e(D)\) gegen verschiedene Zuteilungen der Stichproben in die beiden Gruppen für verschiedene Stichprobengrößen abgebildet.
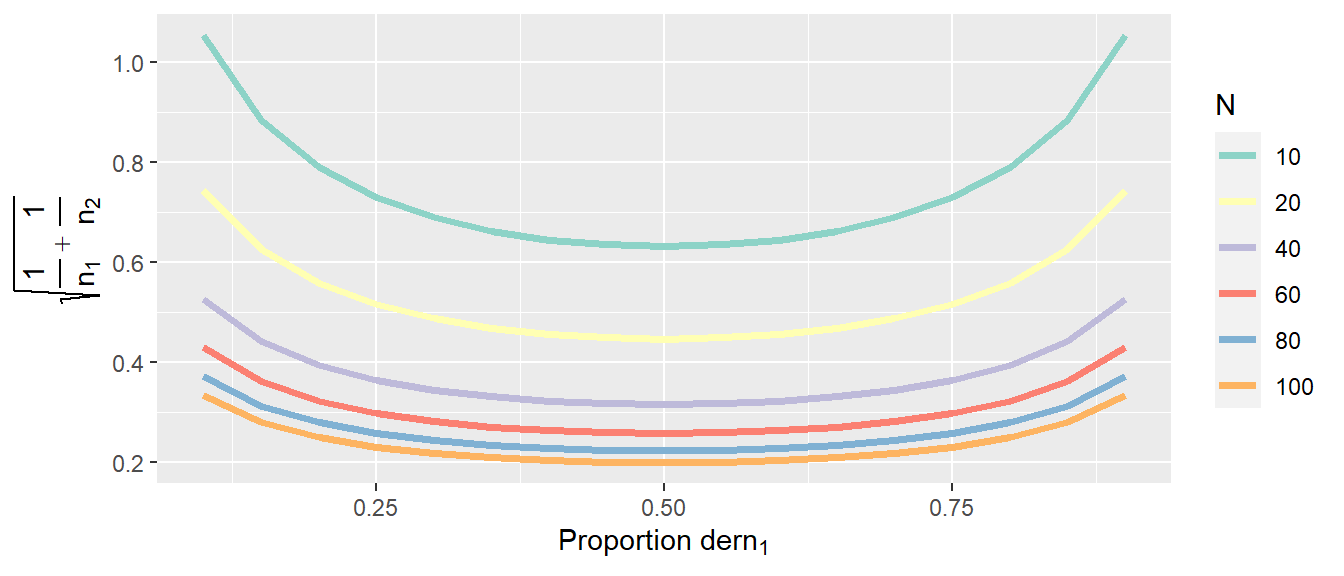
In Abbildung 23.1 ist zu sehen, das das bei gleichen Varianzen die gleichmäßige Verteilung der Stichprobe in die beiden Gruppen immer diejenige mit dem kleinsten Standardfehler ist. Der Standardfehler nimmt natürlich mit der Größe der Stichprobe ab. Allerdings nimmt auch die Größe der Verschlechterung bei ungleicher Verteilung mit der Größe der Stichprobe ab. Daher, wenn wir eine große Stichprobe haben, dann ist die gleichmäßige Verteilung der Stichproben weniger wichtig als bei kleinen Stichprobengrößen.
Schauen wir uns daher als nächsten Fall an, was passiert wenn die Varianzen in den beiden Gruppen nicht mehr gleich sind. Sei zum Beispiel \(\sigma^2 = 1\) und \(\sigma^2 = 9\). Also ein recht extremer Unterschied zwischen den beiden Gruppen.
| \(n_1\) | \(n_2\) | \(\sigma^2(D)\) | \(\sigma_e(D)\) | Effizienz |
|---|---|---|---|---|
| 1 | 11 | 1.82 | 1.35 | 0.73 |
| 2 | 10 | 1.40 | 1.18 | 0.95 |
| 3 | 9 | 1.33 | 1.15 | 1.00 |
| 4 | 8 | 1.38 | 1.17 | 0.97 |
| 5 | 7 | 1.49 | 1.22 | 0.90 |
| 6 | 6 | 1.67 | 1.29 | 0.80 |
| 7 | 5 | 1.94 | 1.39 | 0.69 |
| 8 | 4 | 2.38 | 1.54 | 0.56 |
| 9 | 3 | 3.11 | 1.76 | 0.43 |
| 10 | 2 | 4.60 | 2.14 | 0.29 |
| 11 | 1 | 9.09 | 3.02 | 0.15 |
In Tabelle 23.2 sind wieder die verschiedenen Werte für \(\sigma^2(D)\), \(\sigma_e(D)\) und die Effizienz berechnet worden. Wir können sehen, dass jetzt nicht mehr das Design mit gleich großen Stichproben optimal ist, sondern das Design mit \(n_1 = 3\) und \(n_2 = 9\). Die ungleiche Varianz in den beiden Gruppen hat dazu geführt, dass der minimale Standardfehler dann eingenommen wird, wenn wir eine größere Stichprobe aus Gruppe \(2\) als aus Gruppe \(1\) ziehen.
Wenn wir diese nicht gewusst hätten und in beiden Gruppen wieder mit \(n_i = 6\) gearbeitet hätten, hätten wir somit \(20\%\) Effizienz eingebüßt. Intuitiv macht diese ungleiche Verteilung auch Sinn. Da die Varianz in Gruppe \(2\) größer ist, ist auch unserer Unsicherheit über den Mittelwert in dieser Gruppe größer. Um diese Unsicherheit auszugleichen erhöhen wir die Stichprobenanzahl im Verhältnis zu Gruppe \(1\) um mehr Information über diese Gruppe zu erhalten.
Schauen wir uns ein Beispiel an, bei dem der Unterschied der Varianzen in den beiden Gruppen nicht ganz so extrem ist (siehe Tabelle 23.3).
| \(n_1\) | \(n_2\) | \(\sigma^2(D)\) | \(\sigma_e(D)\) | Effizienz |
|---|---|---|---|---|
| 1 | 11 | 1.18 | 1.09 | 0.41 |
| 2 | 10 | 0.70 | 0.84 | 0.69 |
| 3 | 9 | 0.56 | 0.75 | 0.87 |
| 4 | 8 | 0.50 | 0.71 | 0.97 |
| 5 | 7 | 0.49 | 0.70 | 1.00 |
| 6 | 6 | 0.50 | 0.71 | 0.97 |
| 7 | 5 | 0.54 | 0.74 | 0.89 |
| 8 | 4 | 0.62 | 0.79 | 0.78 |
| 9 | 3 | 0.78 | 0.88 | 0.62 |
| 10 | 2 | 1.10 | 1.05 | 0.44 |
| 11 | 1 | 2.09 | 1.45 | 0.23 |
In Tabelle 23.3 sehen wir wieder, das das effizienteste Design nicht gleich große Stichproben in den beiden Gruppen hat, sondern hier würde das Design mit \(n_1 = 5\) und \(n_2 = 7\) den niedrigsten Standardfehler zeigen. Der Verlust an Effizienz bei gleich großen Gruppen wäre hier praktisch zu vernachlässigen. D.h. wenn wir keine genauen Information haben wie sich die Varianzen in den beiden Gruppen verhalten, aber wir keine großen Unterschiede erwarten, dann sind wir mit gleichgroßen Gruppen wahrscheinlich oft gut bedient.
Untersuchen wir die Effizienz noch einmal aus einer anderen Perspektive, nämlich des Budget das uns zur Verfügung steht. Nehmen wir an wir müssen die Untersuchung in einem Speziallabor durchführen und wir haben nur eine begrenzte Zeit zur Verfügung. Wir untersuchen wieder zwei Gruppen bei denen aber die Vorbereitung des Experiment doppelt solange für Gruppe \(2\) dauert im Vergleich zu Gruppe \(1\). Zum Beispiel in Gruppe \(1\) benötigen wir das Labor für eine Stunde während wir für Teilnehmerinnen und Teilnehmer aus Gruppe \(2\) zwei Stunden benötigen. In Gruppe \(2\) ist vielleicht eine spezielle Patientenpopulation bei der wir mehr Zeit einplanen müssen. Wir haben aber nur insgesamt \(24\) Stunden das Labor zu Verfügung. Wir setzen wieder \(\sigma^2 = 1\) an. Wie sollten wir die Gruppengrößen zuteilen?
Wir können jetzt nicht einfach die gleiche Tabelle wie in den obigen Fällen benutzen, da wir unser Zeitbudget beachten müssen. Mit etwas ausprobieren kommen wir zu folgendem Ergebnis.
| \(n_1\) | \(n_2\) | Kosten | \(\sigma^2(D)\) | \(\sigma_e(D)\) | Effizienz |
|---|---|---|---|---|---|
| 22 | 1 | 24 | 1.05 | 1.02 | 0.23 |
| 20 | 2 | 24 | 0.55 | 0.74 | 0.44 |
| 18 | 3 | 24 | 0.39 | 0.62 | 0.62 |
| 16 | 4 | 24 | 0.31 | 0.56 | 0.78 |
| 14 | 5 | 24 | 0.27 | 0.52 | 0.89 |
| 12 | 6 | 24 | 0.25 | 0.50 | 0.97 |
| 10 | 7 | 24 | 0.24 | 0.49 | 1.00 |
| 8 | 8 | 24 | 0.25 | 0.50 | 0.97 |
| 6 | 9 | 24 | 0.28 | 0.53 | 0.87 |
| 4 | 10 | 24 | 0.35 | 0.59 | 0.69 |
| 2 | 11 | 24 | 0.59 | 0.77 | 0.41 |
Wir sehen wieder in Tabelle 23.4, dass eine ungleiche Verteilung in die Gruppen die höchste Effizienz hat. Der Effekt hier, ist dass wir hier eine Balance finden müssen zwischen der größten Anzahl an Teilnehmerinnen und Teilnehmer und der Ungleichheit der Stichprobengrößen.
Zusammenfassend lässt sich sagen, dass bei Vergleichen zwischen zwei Gruppen das Design mit gleich großen Stichproben in beiden Gruppen oft die Beste Wahl ist. In Abhängigkeit davon wie sich die Varianzen zwischen den Gruppen verhalten und oder auch welche Randbedingungen für die Durchführung des Experiment bestehen, kann ein optimales Design jedoch auch sehr unterschiedlich ausfallen. Daher macht es Sinn für den jeweiligen speziellen Fall sich Gedanken zu machen welches Design den bestmöglichen Output liefert und vielleicht nicht einfach nur ein Standarddesign aus der Schublade zu nehmen. Die Problematik eine informierte Entscheidung diesbezüglich zu treffen wird in den folgenden Kapitel immer wieder aufgegriffen.
23.2 Terminologie
Zunächst müssen einmal vier Grundbegriffe des experimentellen Designs definiert werden. Diese sind, die Experimentelle Einheit (engl. Experimental unit), die Beobachtungseinheit (engl. observational unit), der Replikationsfaktor (engl. replication) und der Wiederholungsfaktor (engl. repetition bzw. auch Pseudoreplication).
Definition 23.1 (Experimentelle Einheit (EU)) Die experimentelle Einheit bezeichnet das kleinste Objekt, dem eine bestimmte Intervention (engl. treatment) bzw. experimentelle Kondition zugewiesen wird. Die Zuweisung muss zufällig (randomisiert) stattfinden. Daher werden im englischen experimentelle Einheiten auch als unit of randomisation bezeichnet. Die Intervention bzw. die Kondition muss unabhängig von anderen experimentellen Einheiten ausgeführt werden. D.h. die EUs dürfen sich nicht gegenseitig beeinflussen können. Die Gesamtzahl der experimentellen Einheiten bestimmt die Stichprobengröße des Experiments.
Die Anforderung von zufällig und unabhängig können sich dabei gegen seitig überschreiben . Werden z.B. acht Personen zufällig auf zwei Konditionen verteilt und die jeweils vier Personen führen die Konditionen gemeinsam in einer Gruppe aus, dann wird das Treatment nicht mehr unabhängig verabreicht. Das führt dazu, dass die beiden Gruppen jeweils zu einer EU zusammengefasst werden müssen. D.h. die Stichprobengröße ist nicht \(N = 8\) sondern \(N = 2\).
Definition 23.2 (Beobachtungseinheit (OU)) Die Beobachtungseinheit ist das Objekt, an der eine Messung vorgenommen wird. Die Beobachtungseinheit kann gleich der experimentellen Einheit sein, kann sich aber auch von dieser unterscheiden. Im Englischen wird auch von der sampling unit bzw. der measurement unit gesprochen.
Wird zum Beispiel ein Experiment mit \(10\) Teilnehmerinnen durchgeführt. Jede Person wird nur einmal gemessen, dann werden entsprechend insgesamt \(10\) Beobachtungseinheiten erhalten. In diesem Fall sind die Beobachtungseinheiten gleich den experimentellen Einheiten. Wird dagegen jede Person an jedem Tag mehrmals, z.b. \(5\)-mal, gemessen, dann werden insgesamt \(5 \cdot 10 = 50\) Beobachtungseinheiten. In diesem Fall sind die experimentellen Einheiten und die Beobachtungseinheiten nicht mehr identisch.
Definition 23.3 (Replikation) Eine Replikation ist die Wiederholung der Versuchssituation durch mehrere experimentelle Einheiten. Unter Replikationen wird daher verstanden, wenn die selben Bedingungen der experimentellen Kondition mit unterschiedlichen experimentellen Einheiten durchgeführt werden. Im englischen wird dieser Wiederholung der Kondition mit mehreren EUs als replications bezeichnet.
Seien beispielsweise \(EU = 9\) experimentelle Einheiten zufällig und unabhängig auf \(K = 3\) Konditionen zugewiesen. D.h. jede Kondition wird dreimal mit unterschiedlichen experimentellen Einheiten wiederholt. Dadurch ist der Replikationsfaktor gleich drei. Der Wert der gemessene abhängigen Variable schwankt dabei zwischen den Replikationen aufgrund von Änderungen, Störvariablen und inhärenten Unterschieden in den experimentellen Einheiten. Daher liefert die Replikation Informationen über die Restvarianz innerhalb der Konditionen. Andersherum ohne Replikationen kann keine Aussage über die zu erwartende Streuung innerhalb einer Kondition getroffen werden. Der Begriff Replikation ist hierbei nicht zu verwechseln mit Replikation eines Befunds in Bezug auf ein Experiment (Replication crisis). Damit wird ein fundamental anderer Prozess leider mit der gleichen Begrifflichkeit bezeichnet.
In Bezug auf die tatsächliche Stichprobengröße ist der Replikationsfaktor zentral. Dieser kann gleich der Anzahl der Personen multipliziert mit der Anzahl der Konditionen sein, wie aber gleich gezeigt ist, ist dies nicht immer der Fall.
Definition 23.4 (Wiederholung/Pseudoreplikation) Wenn die experimentelle Einheit nach der Applikation des Treatments bzw. der Kondition in mehrere Einheiten aufgeteilt wird, spricht man von einer Untereinheit. Dies könnten z.B. mehrere Messungen an einer Versuchsperson sein. Die Messungen an Untereinheiten derselben experimentellen Einheit sind in der Regel korreliert und daher nicht unabhängig voneinander. Im englischen werden diese Einheiten als repetitions bezeichnet.
23.2.1 Beispiele
In Tabelle 23.5 ist ein Beispiel für ein einfaches experimentelles Design dargestellt. Es wurden insgesamt \(9\) TeilnehmerInnen zufällig auf \(3\) Konditionen \(A_1, A_2, A_3\) verteilt. Auf jeder Person wurde eine Messung unter der entsprechenden Kondition durchgeführt und jede Person ist einzeln untersucht worden.
| Teilnehmer | \(A_1\) | \(A_2\) | \(A_3\) |
|---|---|---|---|
| P1 | X | ||
| P2 | X | ||
| P3 | X | ||
| P4 | X | ||
| P5 | X | ||
| P6 | X | ||
| P7 | X | ||
| P8 | X | ||
| P9 | X |
Was sind in diesem Fall die EU und OUs und was ist der Replikationsfaktor und der Wiederholungsfaktor? Die Personen sind randomisiert den verschiedenen Konditionen zugewiesen worden und das treatment erfolgt unabhängig von allen anderen Personen. Daher stellen die Versuchspersonen die EUs dar. Somit folgt \(N = 9\). Da auf jeder Person nur eine Messung erfolgt, resultieren daraus insgesamt \(9\) OUs. D.h. die experimentellen Einheiten und die Beobachtungseinheiten sind in diesem Design identisch. Jede Kondition wurde dreimal durch unabhängige EUs repliziert, daher ist der Replikationsfaktor \(3\). Es wurde keine Wiederholungen auf den EUs durchgeführt, daher ist der Wiederholungsfaktor gleich eins. Dadurch das drei Replikationen für jede Kondition vorhanden sind, kann die Residualvarianz von der Treatmentvarianz unterschieden werden.
In Tabelle 23.6 ist ein ähnliches Untersuchungsdesign dargstellt. Im Unterschied zu Tabelle 23.5 sind auf jeder Person nun zwei Messungen durchgeführt worden.
| Teilnehmer | \(A_1\) | \(A_2\) | \(A_3\) |
|---|---|---|---|
| P1 | X X | ||
| P2 | X X | ||
| P3 | X X | ||
| P4 | X X | ||
| P5 | X X | ||
| P6 | X X | ||
| P7 | X X | ||
| P8 | X X | ||
| P9 | X X |
Dadurch sind immer noch die \(EU = 9\) aber der Replikationsfaktor ist nun gleich zwei. Die Beobachtungseinheiten sind jetzt verdoppelt daraus folgt \(OU = 18\) und ein Pseudoreplikationsfaktor von zwei. Dadurch, dass auf jeder EU zwei Messungen durchgeführt wurden, kann die Präzision der Gesamtmessungen auf den einzelnen EUs erhöht werden. Dadurch wird sich die Varianz die auf die Messmethode zurück zu führen ist reduzieren und es können kleinere Unterschiede zwischen den Treatments identifiziert werden.
Im nächsten Design wird es nun etwas komplizierter. Es sollen drei verschiedene Treatments \(A_1, A_2\) und \(A_3\) mit insgesamt neun Studienteilnehmern untersucht werden. Die Teilnehmer wurden aus drei verschiedenen Vereinen akquiriert. Als Randbedingung die Treatments immer nur einheitlich pro Verein angewendet werden. D.h. alle Teilnehmer aus einem Verein erhalten das gleiche Treatment. Die Zuordnung der Treatments auf die Vereine erfolgt jedoch randomisiert. Es ergibt sich die folgende Designstruktur Tabelle 23.7.
| Teilnehmer | \(A_1\) | \(A_2\) | \(A_3\) | |
|---|---|---|---|---|
| Verein I | P1 | X | ||
| P2 | X | |||
| P3 | X | |||
| Verein II | P4 | X | ||
| P5 | X | |||
| P6 | X | |||
| Verein III | P7 | X | ||
| P8 | X | |||
| P9 | X |
In diesem Fall erfolgt die Zuweisung der Treatments also nicht auf dem Level der Teilnehmer, sondern auf dem Level der drei Vereine. Dies führt nun dazu, da die experimentellen Einheiten laut der Definition die Treatment randomisiert zugewiesen bekommen müssen, dass die Vereine zu den experimentellen Einheiten werden und nicht mehr die einzelnen Teilnehmer. Folgerichtig ist \(N\) ist diesem Fall \(N = 3\) und nicht \(N = 9\) wie in den beiden vorhergehenden Fällen. Dies führt weiterhin dazu, dass keine Replikation der experimentellen Einheiten vorliegt, da jede Kondition nur einmal unter eine experimentellen Einheit beobachtet wurde. Daraus folgt, dass es nicht mehr möglich ist die Ergebnisse über die Studiengruppe hinaus zu generalisieren, da keine ausreichend große Stichprobe gezogen wurde. Zusätzlich und noch wichtiger, da nur eine einzelne experimentelle Einheit beobachtet wurde, können keine Aussagen über die Varianz zwischen experimentellen Einheiten getroffen werden. Die Unterschiede zwischen den Kondition können nicht von der Residualvarianz getrennt werden. Die drei Teilnehmer innerhalb der jeweiligen Vereine werden als Pseudoreplikationen mit einem Faktor von \(3\) interpretiert. Da insgesamt neun Messungen beobachten werden, resultieren daraus neun Beobachtungseinheiten.
Um aus den Teilnehmern tatsächlich auch neun experimentelle Einheiten zu machen, müssen die Treatments unabhängig von den Vereinen auf die Personen randomisiert werden. Zusätzlich muss auch noch sichergestellt werden, das das Treatment in Isolation durchgeführt wird. Der Definition folgend, das jeweilige Treatment muss unabhängig von den anderen experimentellen Einheiten durchgeführt werden. D.h. es können keine Gruppen gebildet werden die beispielsweise gemeinsam trainieren, da es dadurch auch wieder zu ungewollten Interaktionseffekten zwischen den experimentellen Einheiten kommen kann. Dies führt dann wieder dazu, dass jede Gruppe zu einer einzelnen experimentellen Einheit zusammengefasst wird mit der entsprechenden Reduktion in der Stichprobengröße. Die Nichtbeachtung von Abhängigkeiten zwischen experimentellen Einheiten führt in der Analyse zu fehlerhaften Ergebnisse die insbesondere zu einer Vergrößerung des Type-I Fehler führen. D.h. Ergebnisse werden zu oft als statistisch signifikant deklariert (Hurlbert (1984), Lazic, Clarke-Williams, und Munafò (2018), Silverman (2004)).
In Tabelle 23.8 ist ein sogenanntes Repeated measures design. Hier wurden sechs Personen auf zwei Konditionen (CON und TRT) aufgeteilt.
| ID | Condition | PRE | POST | RETENTION |
|---|---|---|---|---|
| P1 | CON | X | X | x |
| P2 | CON | X | X | X |
| P3 | TRT | X | X | X |
| P4 | TRT | X | X | X |
| P5 | CON | X | X | X |
| P6 | TRT | X | X | X |
In diesem Fall ist die Anzahl der EU gleich sechs mit einem Replikationsfaktor drei. Die Beobachtungseinheiten sind die einzelnen Messungen wobei hier keine Pseudoreplikation vorkommen, da die Messungen zu unterschiedlichen Zeitpunkten gewollt sind. Eine Besonderheit ist hier, dass die Messzeitpunkte nicht randomsiert sind sondern in einer vorgegebenen Abfolge stattfinden. Dies muss dann im Rahmen der statistischen Modellierung berücksichtigt werden, hat aber nichts mit der Einteilung in EUs, OUs und Replikation zu tun.
23.3 Implikationen
Die Anzahl der Replikationen der EU bestimmt die Präzision des experimentellen Fehlers \(\sigma^2\) in der jeweiligen Untersuchung. Seien zum Beispiel zwei EUs welche das gleiche Treatment zugewiesen bekommen haben, z.B. zwei Athletinnen. Wenn nun eine Messung durchgeführt wird, z.B. die Sprungleistung beim Counter Movement Jump wird bestimmt, dann wird sich die Sprungleistung zwischen den beiden Athletinnen üblicherweise einfach schon auf Grund der Inter-individuellen Unterschiede zwischen Personen unterscheiden. Es sei zunächst vernachlässigt, dass bei biologischen System selbst schon bei Wiederholung der gleichen Messung zum Teil bedeutsame Unterschiede auftreten können. Die Unterschiede zwischen den Messungen der beiden Athletinnen spiegeln den experimentellen Fehler wieder. Im Sinne des generellen linearen Modells ist dies der Residualfehler \(\epsilon_i\). Umso mehr Replikationen vorliegen, umso präziser kann dieser experimentelle Fehler bestimmt werden. D.h. mit Hilfe der Replikation wird versucht, die Präzision (\(\widehat{=}\) Unsicherheit) in Bezug auf die Konditionen, die sich im Residualfehler ausdrückt, zu verkleinern.
Dies ist grundsätzlich ein anderer Prozess, als derjenige, der durch die Anzahl der Wiederholungen adressiert wird. Die Wierholungen zielen im Gegensatz zur Replikationen dagegen darauf ab, die Streuung innerhalb der EUs zu minimieren. Zum Beispiel wenn die Athletinnen nicht nur einmal sondern mehrere Sprünge durchführen. Dadurch wir die Abschätzung der Sprungleistung der einzelnen Athletinnen verbessert.
Versuchen wir diese beiden Beiträge etwas zu formalisieren. Seien drei verschiedene Varianzkomponenten gegeben. 1) die Varianz zwischen den Athletinnen \(\sigma_{\text{Person}}^2\), 2), die Varianz innerhalb der jeweiligen Athleting \(\sigma_{\text{innerhalb}}^2\) und dann noch eine Residualstreuung die auf zufällige Einflüsse zurück zu führen ist \(\sigma_{\epsilon}^2\). Die Gesamtvarianz \(\sigma_{\text{total}}^2\) die nun bei den Messungen der Sprunghöhen beobachten werden, können nun als die Summe dieser drei Komponenten interpretiert werden (Eine Annahme dabei ist, dass sich die Komponenten untereinander nicht beeinflussen also unabhängig voneinander sind).
\[\begin{equation} \sigma_{\text{total}}^2 = \sigma_{\text{Person}}^2 + \sigma_{\text{innerhalb}}^2 + \sigma_{\epsilon}^2 \end{equation}\]
Diese Gleichung beschreibt die Varianzkomponenten innerhalb einer Treatmentstufe. Wenn nun EUs aus unterschiedlichen Treatmentstufen \(\tau_i\) zusammengesteckt werden, dann wird die Gleichung entsprechend um diese zusätzliche Varianzkomponente \(\sigma_{\tau}^2\) erweitert.
\[\begin{equation} \sigma_{\text{total}}^2 = \sigma_{\tau}^2 + \sigma_{\text{Person}}^2 + \sigma_{\text{innerhalb}}^2 + \sigma_{\epsilon}^2 \end{equation}\]
Die Idee beim experimentellen Designs ist es nun, ein Design zu finden, dass es ermöglicht diese Komponenten durch eine intelligente Verteilung der Faktorstufen, Replikationen und Wiederholungen möglichst präzise zu bestimmen.
Soll zum Beispiel der Einfluss des Treatment \(\tau_i\) bestimmt werden, dann kann die durch das Treatment entstehende Varianz \(\sigma_{\tau}^2\) mit dem experimentellen Fehler \(\sigma_{\epsilon}^2\) verglichen werden, um zu entscheiden ob die Unterschiede zwischen den Faktorstufen auch wirklich bedeutsam sind. In Pseudoschreibweise:
\[\begin{equation*} \frac{\sigma_{\tau}^2}{\sigma_{\epsilon}^2} \end{equation*}\]
Wird nun aber ein Design gewählt, bei die Varianz innerhalb der Athletinnen \(\sigma_{\text{innerhalb}}^2\) nicht isoliert bestimmen werden kann, dann geht \(\sigma_{\text{innerhalb}}^2\) in \(\sigma_{\epsilon}^2\) auf. D.h. die resultierende Residualvarianz \(\sigma_{\epsilon}^2\) vergrößert sich um die Komponente \(\sigma_{\text{innerhalb}}^2\). Im englischen wird dies als confounded bezeichnet. Die beiden Varianzkomponenten können nicht voneinander getrennt werden. Wird nun wieder \(\sigma_{\tau}^2\) mit \(\sigma_{\epsilon}^2\) verglichen, dann fällt dass Verhältnis entsprechend kleiner aus.
\[\begin{equation*} \frac{\sigma_{\tau}^2}{\sigma_{\epsilon^*}^2} = \frac{\sigma_{\tau}^2}{\sigma_{\epsilon}^2 + \sigma_{\text{innerhalb}}^2} \end{equation*}\]
Um diese Betrachtung etwas greifbarer zu machen sei ein einfaches Beispiel mit Zahlen gegeben. Es soll der Unterschied zwischen zwei Konditionen beim CMJ betrachtet, beispielsweise mit (Kondition \(A\)) und ohne (Kondition \(B\)) Vorermüdung. Aus der Literatur oder aus Voruntersuchungen seine die folgenden Werte abzuleiten (siehe Tabelle 23.9}.
| \(\sigma_{\tau}^2\) | \(\sigma_{\text{Person}}^2\) | \(\sigma_{\text{Innerhalb}}^2\) | \(\sigma_{\epsilon}^2\) |
|---|---|---|---|
| 10 | 5 | 3 | 2 |
Wenn das experimentelle Design so gewählt wurde, dass die Unterscheidung der verschiedenen Komponenten möglich ist, dass dann für eine Überprüfung der Unterschiede zwischen den beiden Konditionen das Verhältnis von \(\sigma_{\tau}^2\) zu \(\sigma_{\epsilon}^2\) verwendet werden.
\[\begin{equation*} \frac{\sigma_{\tau}^2}{\sigma_{\epsilon}^2} = \frac{10}{2} = 5 \end{equation*}\]
Es folgt das die Varianz zwischen den Konditionen deutlich (fünfmal) größer ist als die Residualvarianz. Dies kann als ein deutliches Signal dafür betrachtet werden, dass bedeutsame Unterschiede zwischen den Kondition bestehen. Wird nun ein experimentelles Design gewählt, bei dem unabhängige Gruppen miteinander verglichen werden, d.h. die Unterschiede zwischen den Personen \(\sigma_{\text{Person}}^2\) können nicht isoliert werden und es wurde nur eine einzelne Messung durchgeführt womit \(\sigma_{\text{Innerhalb}}^2\) nicht identifizierbar ist, dann führt dies dazu, dass diese Komponenten in der Residualvarianz aufgehen. Es folgt somit wieder für den Vergleich.
\[\begin{equation*} \frac{\sigma_{\tau}^2}{\sigma_{\epsilon}^2} = \frac{\sigma_{\tau}^2}{\sigma_{\text{Person}}^2 + \sigma_{\text{Innerhalb}}^2 + \sigma_{\epsilon}^2} = \frac{10}{5+3+2} = 1 \end{equation*}\]
Somit ist die beobachtete Varianz zwischen den Konditionen gleich der Varianz innerhalb der Konditionen, was eher nicht dazu führen würde, dass die Unterschiede zwischen den Konditionen als bedeutsam interpretiert werden würden
Zusammenfassend sollten diese Betrachtung gezeigt haben, dass bei der Erstellung eines Untersuchungsdesign unterschiedliche Faktoren berücksichtigt werden müssen, um ein optimales experimentelles Design auszuwählen. Die Betrachtungen haben weiterhin gezeigt, dass der übliche Begriff der Stichprobe eigentlich etwas irreführend ist. Im Allgemeinen werden mit der Stichprobe \(N_s\) die Anzahl der Personen die untersucht werden identifiziert. Wie aber durch die Unterscheidung in EU, OU, Replikation und Wiederholung gezeigt wurde, kann die tatsächlich Stichprobe \(N\) je nach Durchführung des Experiment sich deutlich von \(N_s\) unterscheiden. Am dramatischsten war dieser bei dem Beispiel mit den Vereinen zu sehen (siehe Tabelle 23.7), wo eine Erhöhung der Anzahl der Teilnehmerinnen pro Verein zu keine Vergrößerung der Stichprobe geführt hätte.
Im Folgenden wird eine kurze Übersicht über verschiedene Standarddesigns gegeben.
23.4 Übersicht über verschiedene Designs
Das einfachste Design ist ein completely randomized design oder kurz CRD. Wir haben eine unabhängige, nominale Variable \(A\) die verschiedene Faktorstufen (auch Levels) hat. Die EUs werden randomisiert auf die Faktorstufen verteilt und es wird nur eine Messung und somit eine Beobachtungseinheit bestimmt. In diesem Fall können wir auch nur eine Varianzkomponente \(\sigma_{\tau}^2\) bestimmen. In Tabelle 23.10 ist ein Beispiel mit drei Faktorstufen für \(A\) und zwei Replikationen abgebildet.
| EU | \(A_1\) | \(A_2\) | \(A_3\) |
|---|---|---|---|
| 1 | X | ||
| 2 | X | ||
| 3 | X | ||
| 4 | X | ||
| 5 | X | ||
| 6 | X |
Wenn wir nicht mehr nur eine unabhängige Variablen mit verschiedenen Faktorstufen haben, sondern mehrere dann sprechen wir von einen completely randomized factorial design (CRFD). In diesem Fall kommen noch weitere Varianzkomponenten für die jeweiligen unabhängigen Variablen hinzu, sowie mögliche Interaktioneffekte wie wir sie schon abhand der Interaktionen in der multiplen Regression kennengelernt haben. In Tabelle 23.11 ist eine einfacher Fall mit zwei unabhängigen Variablen \(A\) und \(B\) mit jeweils zwei Stufen dargestellt. Damit die Tabelle nicht zu groß wird, ist nur eine Replikation dargestellt.
| \(A_1\) | \(A_2\) | |||
|---|---|---|---|---|
| EU | \(B_1\) | \(B_2\) | \(B_1\) | \(B_2\) |
| 1 | X | |||
| 2 | X | |||
| 3 | X | |||
| 4 | X | |||
Eine weitere Variante ist das sogenannte Completely Randomized Block Design (CRBD). Hier lassen sich die EU in Blöcke gruppieren die ähnlich zueinander sind. In Tabelle 23.12 ist eine einfache Struktur mit vier Blöcken I, II, III und IV abgebildet. Dies könnten zum Beispiel Athleten die in Blöcken von drei aus dem gleichen Verein (Block) kommen. Die Annahme dahinter ist, dass die Vereine dazu führen, dass sich die Athleten aus dem gleichen Verein stärker ähneln als Athleten aus verschiedenen Vereinen. Ein Faktor A hat dabei drei Ausprägungen (A1, A2 und A3) und alle Stufen sind in allen Blöcken enthalten. Die EUs innerhalb eines Blocks werden dabei randomisiert auf die drei Stufen von A verteilt. Daher kommt das randomized.
| Block | \(A_1\) | \(A_2\) | \(A_3\) |
|---|---|---|---|
| I | X | X | X |
| II | X | X | X |
| III | X | X | X |
| IV | X | X | X |
Eine Variante des CRBD ist das Incomplete Block Design (siehe Tabelle 23.13). Hier sind nicht alle Faktorstufen von A in jedem Block vorhanden sondern nur bestimmte Kombinationen die jedoch über die Gesamtzahl balanciert werden.
| Block | \(A_1\) | \(A_2\) | \(A_3\) |
|---|---|---|---|
| I | X | X | |
| II | X | X | |
| III | X | X | |
| IV | X | X | |
| V | X | X | |
| VI | X | X |
Als letztes Design dann noch das Split-Plot Design (SPD). Bei SPD werden ebenfalls zwei Faktoren betrachtet. Die Besonderheit ist hier allerdings, dass die Zuteilung der Faktorstufen bzw. deren Kombination unterschiedlich schwer sind. Im Beispiel lässt sich der Faktor B einfacher zuteilen, während Faktor A schwerer zuzuteilen ist.
| \(A_1\) | \(A_2\) | |||||
|---|---|---|---|---|---|---|
| EU | \(B_1\) | \(B_2\) | \(B_3\) | \(B_1\) | \(B_2\) | \(B_3\) |
| 1 | X | X | X | |||
| 2 | X | X | X | |||
| 3 | X | X | X | |||
| 4 | X | X | X | |||
Ein Beispiel für ein SPD ist eine Treatment-Control Studie. Hier wäre beispielsweise \(A_1\) = Control, \(A_2\) = Treatment und \(B_1\) = pre, \(B_2\) = post und \(B_3\) = retention.
Die verschiedenen Design haben jeweils Stärken und Schwächen wenn es darum geht unterschiedliche Varianzkomponenten zu isolieren die es dann möglich machen für ein gegebenes Problem ein effizientes Design auszuwählen bzw. anzupassen.