12 Weitere Grundlagen der Statistik

In diesem Kapitel werden ein paar übergeordnete Konzepte der Statistik, auf die im späteren Verlauf immer wieder zurückgegriffen wird, noch einmal etwas eingehender behandelt. Dies betrifft vor allem den Begriff des Erwartungswerts und auch noch einmal die Varianz. Dazu wird kurz der Begriff eines Schätzers formalisiert. Am Ende des Kapitels werden in einer Art Liste verschiedene Varianten von Hypothesentests kurz vorgestellt.

12.1 Der Erwartungswert \(\mu\) einer Zufallsvariable

Bisher wurde oft der Begriff Mittelwert verwendet und zum Beispiel vom Mittelwert \(\mu\) einer Normalverteilung gesprochen. Eigentlich ist \(\mu\) nicht nur der Mittelwert, sondern wird als Erwartungswert bezeichnet. Bei einer diskreten Zufallsvariable \(X\), d.h. einer Zufallsvariable, die auf einer endlichen Menge von Ereignissen \(\{x_i, i = 1, \ldots, n\}\) mit \(n\) Elementen definiert ist, ist der Erwartungswert wie folgt definiert:

12.1.1 Erwartungswert \(\mu\)

\[\begin{equation} E[X] = \sum_{i=1}^n x_i P(x_i) \label{eq-stats-hypo-expected-01} \end{equation}\]

Der Erwartungswert wird üblicherweise mit dem Symbol \(\mu\) bezeichnet.

D.h. jedes mögliche Ereignis wird mit seiner Wahrscheinlichkeit multipliziert, und die Summe über alle diese Möglichkeiten wird gebildet, um den Erwartungswert \(\mu\) zu bestimmen.

Beispiel 12.1 (Erwartungswert eines Würfels) Sei ein normaler Würfel mit sechs Seiten gegeben und die Zufallsvariable \(X\) ist die jeweilige Augenanzahl der Würfelseiten. Da bei einem fairen Würfel alle Seiten gleichwahrscheinlich sind, hat jedes Ereignis \(x_i \in \{1,2,3,4,5,6\}\) eine Wahrscheinlichkeit von \(P(X = x) = \frac{1}{6}\). Somit errechnet sich der Erwartungswert.

\[\begin{equation*} E[X] = \sum_{i=1}^6 x_i P(x_i) = 1\cdot\frac{1}{6} + 2\cdot\frac{1}{6} +3\cdot\frac{1}{6} +4\cdot\frac{1}{6} +5\cdot\frac{1}{6} +6\cdot\frac{1}{6} = 3.5 \end{equation*}\]

Tipp

Wenn der Fall auftritt, dass mehrere Zufallsvariablen verwendet werden, z.B. \(X\) und \(Y\), dann wird die folgende Schreibweise verwendet, um die Erwartungswerte voneinander abzugrenzen. Zum Beispiel der Erwartungswert der Zufallsvariable \(X\):

\[ E[X] = \mu_X \] Der Erwartungswert der Zufallsvariable \(X\) wird mit \(\mu_X\) bezeichnet. Wenn der Zusammenhang klar ist und nur von einer bestimmten Zufallsvariablen gesprochen wird, dann auch nur \(\mu\).

In der statistischen Literatur ist es üblich, die Größe \(\mu\) als den Mittelwert der Population zu bezeichnen, auch wenn es sich dabei nicht unbedingt um den Mittelwert handelt, wie er üblicherweise verstanden wird und z.B. bei der Stichprobe berechnet wird (\(\bar{x} = \frac{1}{n}\sum_{i=1}^n x_i\)). Bei dem Erwartungswert \(\mu\) handelt es sich um den gewichteten Mittelwert. Es wird unterschieden zwischen dem Mittelwert in der Population \(\mu\), der theoretisch ist, und dem Mittelwert der Stichprobe \(\bar{X}\), der eine Zufallsvariable darstellt und ebenfalls von theoretischer Natur ist, und dem tatsächlich beobachteten Mittelwert \(\bar{x}\) in der Stichprobe. In den meisten Fällen im alltäglichen Umgang ist diese Unterscheidung nicht von Bedeutung, sondern wird oft erst bei der Herleitung von theoretischen Zusammenhängen wichtig.

Für den späteren Umgang mit dem Erwartungswert ist die Kenntnis von ein paar Rechenregeln notwendig. Diese werden im Folgenden aufgelistet.

Die erste Regel behandelt den Fall, wenn eine Zufallsvariable \(X\) mit einer Konstanten \(a\) multipliziert wird. Konstant bedeutet, dass es sich bei \(a\) nicht um eine Zufallsvariable handelt und \(a\) immer den gleichen Wert hat. D.h. es soll der Erwartungswert von \(aX\) berechnet werden:

\[\begin{equation} E[aX] = \sum_{i=1}^n a x_i P(x_i) = a \sum_{i=1}^n x_i P(x_i) = a E[X] \label{eq-stats-hypo-expected-mult} \end{equation}\]

Beispiel 12.2 (Erwartungswert der Summe der Augenzahl mal \(100\)) Es soll nicht die Augenzahl des Würfels, sondern die Augenzahl mal \(100\) berechnet werden, und davon der Erwartungswert. Somit gilt \(a = 100\) und mit Formel \(\eqref{eq-stats-hypo-expected-mult}\):

\[\begin{equation*} E[aX] = a E[X] = 100 \cdot 3.5 = 350 \end{equation*}\]

In vielen Fällen ist nicht nur eine einzelne Zufallsvariable beteiligt, sondern, beispielsweise wenn eine Stichprobe untersucht wird, liegen mehrere Zufallsvariablen vor. Der einfachste Fall ist dabei natürlich, wenn nur zwei unabhängige Zufallsvariablen \(X\) und \(Y\) benötigt werden. Der allgemeine Fall lässt sich dann aus diesem Spezialfall herleiten. Die beiden Variablen können auf der gleichen Ereignismenge definiert sein, können aber auch auf unterschiedlichen Ereignismengen, z.B. \(\{x_i, i = 1, \ldots, n\}\) und \(\{y_j, j = 1, \ldots, m\}\) definiert sein. Soll der Erwartungswert des Mittelwerts der beiden Zufallsvariablen \(X\) und \(Y\) berechnet werden, kann eine Regel angewendet werden, die die Addition unabhängiger Zufallsvariablen regelt. Tatsächlich ist diese Operation relativ einfach nachzuvollziehen, der Erwartungswert \(E[X + Y]\) berechnet sich mittels:

\[\begin{equation} E[X + Y] = \sum_{i=1}^n x_i P(x_i) + \sum_{j=1}^m y_j P(y_j) = E[X] + E[Y] \label{eq-stats-hypo-expected-add2} \end{equation}\]

Beispiel 12.3 (Erwartungswert der Summe der Augenzahlen zweier Würfel) Sei \(X\) die Augenzahl des einen Würfels (z.B. ein blauer Würfel) und \(Y\) die Augenzahl eines weiteren Würfels (z.B. ein roter Würfel). Dann gilt nach Formel \(\eqref{eq-stats-hypo-expected-add2}\):

\[\begin{equation*} E[X + Y] = E[X] + E[Y] = 3.5 + 3.5 = 7 \end{equation*}\]

Die Formel \(\eqref{eq-stats-hypo-expected-add2}\) als Spezialfall mit nur zwei Zufallsvariablen lässt sich relativ direkt für den Fall von \(n\) unabhängigen Zufallsvariablen \(X_i, i = 1, \ldots, n\) generalisieren. Seien zum Beispiel drei Zufallsvariablen \(X, Y\) und \(Z\) gegeben und der Erwartungswert der Summe \(M = X + Y + Z\) soll berechnet werden, dann lässt sich eine Zwischenvariable, z.B. \(A = Y + Z\), definieren und es gilt \(M = X + A\). Dies ist wieder der bereits bekannte Fall. Wiederholte Anwendung führt dann zur folgenden allgemeinen Regel:

\[\begin{equation} E[X_1 + X_2 + \ldots + X_n] = E[X_1] + E[X_2] + \ldots + E[X_n] \label{eq-stats-hypo-expected-add} \end{equation}\]

In Kombination mit der Regel für konstante Terme (Formel \(\eqref{eq-stats-hypo-expected-mult}\)) mit den Konstanten \(a_1, a_2, \ldots, a_n\) folgt dann eine weitere Verallgemeinerung:

\[\begin{equation} E[a_1 X_1 + a_2 X_2 + \ldots + a_n X_n] = a_1 E[X_1] + a_2 E[X_2] + \ldots + a_n E[X_n] \label{eq-stats-hypo-expected-lo} \end{equation}\]

Diese Eigenschaft, dass der Erwartungswert einer gewichteten Summe von Zufallsvariablen (eine lineare Operation) gleich der gewichteten Summe der einzelnen Erwartungswerte ist, macht den Erwartungswert zu einem linearen Operator.

Nur der Vollständigkeit halber sei auch noch kurz die Definition des Erwartungswertes für reelle Verteilungen erwähnt. Hier ist die Zufallsvariable nicht mehr auf einer endlichen Menge, sondern auf einem Intervall definiert. Auf die Herleitung wird nicht eingegangen, sondern es reicht, das Summenzeichen durch ein Integral zu ersetzen:

\[\begin{equation*} E[X] = \int_{x=-\infty}^\infty x f(x) dx \end{equation*}\]

Das Integral geht über den gesamten Definitionsbereich von \(X\), und die Wahrscheinlichkeitsfunktion wird durch die Dichtefunktion \(f(x)\) ersetzt. Die Linearität der Operation bleibt für alle im Weiteren interessierenden Fälle erhalten (keine Panik, es werden im Weiteren keine Integrale berechnet).

Beispiel 12.4 Sei eine Zufallsvariable \(X\) gegeben, die nur vier verschiedene Werte annehmen kann \(x \in \{0,1,2,3\}\). Diese Ereignisse haben die folgenden Wahrscheinlichkeiten (siehe Tabelle 12.1):

Tabelle 12.1: Verteilung der Zufallsvariablen \(X\)

x	0	1	2	3
\(P(x)\)	\(\frac{1}{8}\)	\(\frac{5}{8}\)	\(\frac{1}{8}\)	\(\frac{1}{8}\)

Anwendung von Formel \(\eqref{eq-stats-hypo-expected-01}\) führt zur Berechnung des Erwartungswerts \(E[X]\) mittels:

\[ E[X] = \sum_{i=1}^4 x_i P(x_i) = 0 \cdot \frac{1}{8} + 1 \cdot \frac{5}{8} + 2\cdot \frac{1}{8} + 3\cdot \frac{1}{8} = 1.75 \]

Beispiel 12.5 Haben wir eine zweite Zufallsvariable \(Y\) mit der Verteilung (siehe Tabelle 12.2)

Tabelle 12.2: Verteilung der Zufallsvariablen \(X\)

y	0	1	2	3
\(P(y)\)	\(\frac{2}{8}\)	\(\frac{2}{8}\)	\(\frac{1}{8}\)	\(\frac{3}{8}\)

Mit Formel \(\eqref{eq-stats-hypo-expected-01}\) folgt wiederum:

\[ E[Y] = \sum_{i=1}^4 y_i P(y_i) = 0 \cdot \frac{2}{8} + 1 \cdot \frac{2}{8} + 2 \cdot \frac{1}{8} + 3 \cdot \frac{3}{8} = 1.625 \]

Wenn wir eine neue Zufallsvariable \(Z\) definieren mit \(Z = X + Y\), dann folgt für den Erwarungswert von \(E[Z] = E[X + Y]\) mittels \(\eqref{eq-stats-hypo-expected-add}\):

\[ E[Z] = E[X + Y] = E[X] + E[Y] = 1.25 + 1.625 = 2.875 \]

Definieren wir dagegen \(Z\) mit \(Z := a \cdot X\) mit der Konstanten \(a := 2\). Dann folgt für den Erwartungswert von \(E[Z]\) mit Formel \(\eqref{eq-stats-hypo-expected-mult}\):

\[ E[Z] = E[aX] = aE[X] = 2 \cdot 1.25 = 2.5 \]

Beispiel 12.6 (Chuck-a-Luck) Ein ganz anderes Beispiel, das noch einmal den Begriff Erwartungswert veranschaulicht, bezieht sich auf ein Glücksspiel mit dem Namen Chuck-a-Luck. Das Beispiel ist Gross, Harris, und Riehl (2019) entnommen. Chuck-a-Luck wird mit einem Einsatz von 1 € gespielt. Es werden drei Würfel geworfen, und die folgenden Regeln bestimmen den Gewinn (siehe Tabelle 12.3).

Tabelle 12.3: Gewinnausschüttung bei Chuck-a-Luck

Ausgang	Gewinn
keine 6	0 €
min. eine 6	2 €
3 x 6	27 €

Die Frage, die sich nun stellt, ist, ob dieses Spiel fair ist bzw. ob es sich lohnt, einen 1-€-Einsatz zu setzen. Diese Frage kann mit dem Erwartungswert beantwortet werden. Um den Erwartungswert zu berechnen, benötigen wir allerdings zunächst die Wahrscheinlichkeiten für die verschiedenen Ausgänge.

Die Wahrscheinlichkeit, keine \(6\) zu werfen, ist für jeden Würfel einzeln \(\frac{5}{6}\). Da die Würfel unabhängig voneinander sind, kann diese Wahrscheinlichkeit dreimal miteinander multipliziert werden.

\[ P(0 \times 6) = \left(\frac{5}{6}\right)^3 = \frac{125}{216} \approx 0.579 \]

D.h. in knapp 60 % der Fälle wird bei dem Spiel kein Gewinn ausgeschüttet. Berechnen wir nun den Fall, dass drei Sechsen geworfen werden. Dieser Fall kann parallel zu demjenigen für keine Sechs gelöst werden. Einziger Unterschied ist die Wahrscheinlichkeit des Ereignisses. Die Wahrscheinlichkeit, für einen Würfel eine Sechs zu würfeln, ist \(\frac{1}{6}\). Es folgt daher analog:

\[ P(3 \times 6) = \left(\frac{1}{6}\right)^3 = \frac{1}{216} \approx 0.005 \]

D.h. die Wahrscheinlichkeit für \(3 \times 6\) beträgt gerade einmal ein halbes Prozent. D.h. in 200 Spielen erwarten wir dieses Ereignis nur ein einziges Mal.

Letztlich bleibt noch das Ereignis „mindestens eine \(6\)“. Hier nehmen wir das Komplementärereignis zu „mindestens eine Sechs“. Das Komplementärereignis ist, keine Sechs zu würfeln. Diese Wahrscheinlichkeit ziehen wir dann von 1, dem sicheren Ereignis, ab. Da diese Menge auch die drei Sechsen beinhaltet, für die eine andere Gewinnberechnung gilt, müssen wir deren Wahrscheinlichkeit noch subtrahieren.

\[ P(\text{min. eine } 6) = 1 - P(0 \times 6) - P(3 \times 6) = \frac{216}{216} - \frac{125}{216} - \frac{1}{216} = \frac{90}{216} = 0.41\bar{6} \]

Die Wahrscheinlichkeit für mindestens eine Sechs beträgt dementsprechend etwas über 40 %. Jetzt wenden wir wieder die Formel für den Erwartungswert an, um die zu erwartende Gewinnsumme zu bestimmen. Die Gewinnsumme nimmt jetzt den Wert der Zufallsvariablen ein.

\[ E[X] = \frac{125}{216} \times 0 + \frac{90}{216} \times 2 + \frac{1}{216} \times 27 = \frac{207}{216} \approx 0.958 \]

Im Mittel erwarten wir bei dem Spiel einen Gewinn von \(0.958\) € bei einem Einsatz von \(1\) €. Daher wird im Mittel ein Verlust bei dem Spiel gemacht.

Beispiel 12.7 Als letztes Beispiel betrachten wir den Erwartungswert des Mittelwerts \(\bar{X}\) von \(n\) identisch verteilten Zufallsvariablen \(X_i\). Dadurch, dass für alle \(X_i, E[X_i] = \mu\) gilt, ist dies letztendlich nur eine direkte Anwendung der obigen Rechenregeln.

\[\begin{equation} E[\bar{X}] = E\left[\frac{1}{n}\sum_{i=1}^n X_i\right] = \frac{1}{n}E\left[\sum_{i=1}^n X_i\right] = \frac{1}{n}\sum_{i=1}^n E[X_i] = \frac{1}{n}\sum_{i=1}^n \mu = \frac{1}{n}n \mu = \mu \label{eq-stats-hyp-exbar} \end{equation}\]

D.h. der Erwartungswert des Mittelwerts ist tatsächlich auch der Erwartungswert \(\mu\) der Verteilung.

12.2 Die Varianz \(\sigma^2\) einer Zufallsvariablen

Die Varianz \(\sigma^2\) beschreibt die Streuung der Zufallsvariablen \(X\).

12.2.1 Varianz \(\sigma^2\)

\[\begin{equation} Var(X) = \sigma^2 = E[(X-E[X])^2] = E[(X - \mu)^2] \label{eq-def-variance} \end{equation}\]

D.h. die Varianz ist die quadrierte Abweichung von \(X\) vom Erwartungswert \(\mu\).

Wie wir schon behandelt haben, wird die Varianz als Skalenparameter bezeichnet. In den meisten Fällen arbeiten wir jedoch mit der Standardabweichung \(\sigma\), da diese die gleichen Einheiten wie die Variable \(X\) hat.

Wenn wir den quadratischen Term ausmultiplizieren und dabei die Rechenregeln für den Erwartungswert berücksichtigen (\(E[X] = \mu\) wird als eine Konstante betrachtet), dann erhalten wir eine praktische, alternative Formulierung für die Varianz \(\sigma^2\).

\[\begin{align*} \sigma^2 &= E[(X-E[X])^2] \\ &= E[X^2 + E[X]^2 - 2XE[X]] \\ &= E[X^2] - E[E[X]^2] - E[2E[X]X] \\ &= E[X^2] - E[X]^2 - 2E[X]E[X] \\ &= E[X^2] - E[X]^2 - 2E[X]^2 \\ &= E[X^2] - E[X]^2 \end{align*}\]

Bzw.

\[\begin{equation} Var(X) = \sigma^2 = E[X^2] - \mu^2 \label{eq-stats-hypo-var2} \end{equation}\]

Die Gleichung \(\eqref{eq-stats-hypo-var2}\) wird später immer wieder praktisch sein, wenn wir die Eigenschaften von bestimmten Statistiken formal bestimmen wollen.

Für die Varianz gibt es auch paar einfache Rechenregeln ähnlich wie für den Erwartungswert. Für eine Konstante \(a\) gilt

\[\begin{align*} Var(a) &= 0 \\ Var(a + X) &= Var(X) \\ Var(a \cdot X) &= a^2 \cdot Var(X) \end{align*}\]

Insgesamt gilt für die Linearkombination von \(n\) unabhängigen Zufallsvariablen \(X_i\):

\[\begin{equation} Var\left(\sum_{i=1}^n a_i X_i\right) = \sum_{i=1}^n a_i^2 Var(X_i) \label{eq-stats-hypo-sum-var} \end{equation}\]

Beispiel 12.8 Für zwei unabhängige Zufallsvariablen \(X\) und \(Y\) gilt:

\[\begin{equation*} Var(X + Y) = Var(X) + Var(Y) \end{equation*}\]

In der Rechenregel wurde der Begriff “unabhängig” verwendet, der bisher noch nicht definiert wurde. Da die Unabhängigkeit ein zentrales Konzept in der Statistik ist, wird dies etwas weiter unten noch einmal spezifischer aufgegriffen. Zunächst reicht jedoch ein intuitives Verständnis von Unabhängigkeit im Sinne davon, dass Variablen keinen Einfluss aufeinander haben.

Beispiel 12.9 Eine überraschende Eigenschaft aus den Rechenregeln für die Varianz ist, dass die Varianz der Differenz zweier unabhängiger Variablen gleich der Varianz ist, wie wenn die beiden Variablen miteinander addiert werden.

\[\begin{equation} \begin{split} Var(X - Y) &= Var(1 \cdot X + (-1) \cdot Y) \\ &= Var(X) + Var((-1) \cdot Y) \\ &= Var(X) + (-1)^2 \cdot Var(Y) \\ &= Var(X) + Var(Y) \end{split} \label{eq-stats-hypo-vardiff} \end{equation}\]

Das Ergebnis in Formel \(\eqref{eq-stats-hypo-vardiff}\) wird im späteren Verlauf immer wieder auftauchen, beispielsweise im Rahmen von experimentellen Untersuchungsdesigns.

Beispiel 12.10 Mit den obigen Regeln können wir auch die Varianz des Mittelwerts \(\bar{X}\) bestimmen. Die Variablen \(X_i, i = 1,\ldots,n\) seien wieder unabhängig voneinander und stammen aus der gleichen Verteilung mit \(Var(X_i) = \sigma^2\).

\[\begin{equation} \begin{split} Var(\bar{X}) &= Var\left(\frac{1}{n}\sum_{i=1}^n X_i\right) \\ &= \left(\frac{1}{n}\right)^2 Var\left(\sum_{i=1}^n X_i\right) \\ &= \frac{1}{n^2}\sum_{i=1}^n Var(X_i) \\ &= \frac{1}{n^2}\sum_{i=1}^n \sigma^2 \\ &= \frac{1}{n^2}n \sigma^2 = \frac{\sigma^2}{n} \end{split} \label{eq-stats-hypo-barxse} \end{equation}\]

Die Gleichung \(\eqref{eq-stats-hypo-barxse}\) sollte uns bekannt vorkommen, da sie der Standardfehler des Mittelwerts bzw. die Varianz dessen ist. Hier sehen wir den Wurzelzusammenhang, den wir bereits beobachtet haben. Formal haben wir daher hergeleitet, dass die Streuung des Mittelwerts einer Stichprobe mit der Wurzel der Stichprobengröße \(n\) abnimmt.

Wie beim Erwartungswert betrachten wir auch hier kurz die kontinuierliche Version der Definition der Varianz.

\[\begin{equation} Var(X) = \int_{-\infty}^{\infty}(X-\mu)^2 f(x) dx \end{equation}\]

12.3 Kovarianz \(Cov(X,Y)\)

Die Kovarianz ist ein weiteres zentrales Konzept in der Statistik. Wie die sprachliche Nähe zur Varianz andeutet, sind die beiden Konzepte miteinander verwandt.

Definition 12.1 (Kovarianz) Die Kovarianz \(Cov(X,Y)\) ist ein statistisches Maß, das die lineare Beziehung zwischen zwei Zufallsvariablen \(X\) und \(Y\) beschreibt. Die Kovarianz gibt an, wie stark und in welche Richtung sich die beiden Zufallsvariablen gemeinsam verändern.

In der Population wird für die Kovarianz das Symbol \(\sigma_{xy}\) verwendet.

Ist die Kovarianz positiv, bedeutet dies, dass hohe Werte der einen Variablen tendenziell mit hohen Werten der anderen Variablen einhergehen. Eine negative Kovarianz hingegen weist darauf hin, dass hohe Werte einer Variablen mit niedrigen Werten der anderen Variablen zusammenhängen. Liegt die Kovarianz bei null, gibt es keine lineare Abhängigkeit zwischen den Variablen, was jedoch nicht ausschließt, dass andere (z. B. nicht-lineare) Beziehungen bestehen können.

Mathematisch wird die Kovarianz durch den Erwartungswert des Produkts der Abweichungen der Variablen von ihren jeweiligen Erwartungswerten berechnet. Seien zwei Zufallsvariablen \(X\) und \(Y\) gegeben, dann berechnet sich die Kovarianz \(Cov(X,Y)\) nach:

\[\begin{equation} \text{Cov}(X, Y) = \sigma_{xy} = E[(X - \mu_X)(Y - \mu_Y)], \label{eq-stats-hypo-cov-def} \end{equation}\]

Das Ausmultiplizieren der Terme und die Anwendung der Rechenregeln für den Erwartungswert führen zu folgender alternativer Darstellung, mit der oft einfacher gearbeitet werden kann:

\[\begin{equation*} \sigma_{xy} = E[XY] - E[X]E[Y] \end{equation*}\]

Die Kovarianz hat die Einheit des Produkts der Variablen, was sie oft schwer interpretierbar macht, wenn die Variablen unterschiedliche Skalen haben. In der allgemeinen Anwendung spielt die Kovarianz, ähnlich wie die Varianz, eher eine untergeordnete Rolle, ist aber in der Herleitung von Gesetzmäßigkeiten zentral.

Die Kovarianz einer Variable \(X\) mit sich selbst ist die Varianz:

\[\begin{equation*} \text{Cov}(X,X) = E[(X-\mu_X)(X-\mu_X)] = E[(X-\mu_X)^2] = \text{Var}(X) \end{equation*}\]

Die Kovarianz zwischen Variablen wird oft in Form einer Kovarianzmatrix dargestellt. Seien wieder die beiden Zufallsvariablen \(X\) und \(Y\) gegeben, dann kann die folgende Kovarianzmatrix erstellt werden:

\[\begin{equation*} \text{Cov}(X,Y) = \begin{pmatrix} \sigma_X^2 & \sigma_{XY} \\ \sigma_{XY} & \sigma_Y^2 \end{pmatrix} \end{equation*}\]

D.h. auf der Hauptdiagonalen stehen die Varianzen der beiden Variablen, während die anderen beiden Elemente jeweils die Kovarianz angeben. Da \(Cov(X,Y) = Cov(Y,X)\) gilt, sind die beiden Elemente gleich, und es handelt sich um eine symmetrische Matrix. Kovarianzmatrizen werden oft mit dem Symbol \(\Sigma\) bezeichnet.

Wenn mehr als zwei Zufallsvariablen beteiligt sind, erweitert sich die Kovarianzmatrix entsprechend. Zum Beispiel bei drei Zufallsvariablen \(X, Y\) und \(Z\).

\[\begin{equation*} \Sigma = \begin{pmatrix} \sigma_x^2 & \sigma_{xy} & \sigma_{xz} \\ \sigma_{xy} & \sigma_{y}^2 & \sigma_{yz} \\ \sigma_{xz} & \sigma_{yz} & \sigma_{z}^2 \end{pmatrix} \end{equation*}\]

12.3.1 Kovarianz in `R`

In R kann die Kovarianz von Variablen mittels der Funktion cov() berechnet werden.

x <- rnorm(10) 
y <- rnorm(10) 
cov(x,y)

[1] 0.4534518

Um eine Kovarianzmatrix zu erhalten müssen die Daten in Form einer Matrix an die Funktion übergeben werden.

cov(cbind(x,y))

          x         y
x 0.8528331 0.4534518
y 0.4534518 0.9095998

Sollen dagegen multivariate Zufallsvariablen mit einer gegebene Kovarianzstruktur erzeugt werden, dann kann für normalverteilte Variablen die Funktion mvrnorm() aus dem package MASS verwendet werden.

mu_s <- 1:2
sigma <- matrix(c(0.4,0.2,0.2,0.5), nr=2)
MASS::mvrnorm(n = 3, mu = mu_s, Sigma = sigma)

          [,1]     [,2]
[1,] 0.4570861 1.233114
[2,] 1.9741296 1.195610
[3,] 0.3136756 1.911691

Hier wurden drei Zufallsstichproben mit jeweils zwei Elementen erzeugt, basierend auf einer multivariaten Normalverteilung mit \(\mu = [1,2]\) und der Kovarianzmatrix.

\[\begin{equation*} \Sigma = \begin{pmatrix} 0.4 & 0.2 \\ 0.2 & 0.5 \\ \end{pmatrix} \end{equation*}\]

12.4 Statistische Unabhängigkeit

Unabhängigkeit ist ein fundamentales Konzept in der Statistik und beschreibt eine vollständige Abwesenheit eines Zusammenhangs zwischen zwei Zufallsvariablen. Zwei Variablen \(X\) und \(Y\) sind unabhängig, wenn das Eintreten eines bestimmten Wertes oder Ereignisses der einen Variablen keinen Einfluss auf die Wahrscheinlichkeitsverteilung der anderen Variablen hat.

Definition 12.2 (Statistische Unabhängigkeit) Statistische Unabhängigkeit beschreibt eine Beziehung zwischen zwei Ereignissen oder Zufallsvariablen. Zwei Ereignisse bzw. Zufallsvariablen sind unabhängig voneinander, wenn das Eintreten des einen Ereignisses oder der Wert der einen Variablen keinen Einfluss auf das Eintreten oder den Wert des anderen Ereignisses bzw. der anderen Zufallsvariablen hat.

Formal ausgedrückt bedeutet dies, dass ihre gemeinsame Verteilung durch das Produkt ihrer einzelnen (marginalen) Verteilungen dargestellt werden kann:

\[\begin{equation} P(X \cap Y) = P(X) \cdot P(Y) \label{eq-stats-hypo-independence} \end{equation}\]

Beispiel 12.11 Wenn ein Experiment mit zwei Würfeln durchgeführt wird, dann hat der Ausgang des einen Würfelwurfs keinen Einfluss auf das Ergebnis des anderen Würfelwurfs. Seien die Würfel farblich zu unterscheiden, z.B. blau (\(X\)) und grün (\(Y\)), dann ist die Wahrscheinlichkeit, mit dem blauen Würfel eine Sechs zu würfeln, vollkommen unbeeinflusst vom Ausgang des anderen Würfels. Umgekehrt ist die Wahrscheinlichkeit, mit dem grünen Würfel eine Eins zu würfeln, unbeeinflusst vom Ausgang des anderen Würfels. Formal:

\[\begin{equation*} P(X = 6 \cap Y = 1) = P(X=6) \cdot P(Y=1) = \frac{1}{6} \cdot \frac{1}{6} = \frac{1}{36} \end{equation*}\]

Unabhängigkeit ist eine stärkere Bedingung als die Abwesenheit linearer Beziehungen, wie sie durch eine Kovarianz von null ausgedrückt wird. Tatsächlich impliziert Unabhängigkeit, dass die Kovarianz zwischen \(X\) und \(Y\) gleich null ist. Das Umgekehrte gilt jedoch nicht: Eine Kovarianz von null bedeutet lediglich, dass keine lineare Beziehung besteht; es könnten dennoch komplexere, nicht-lineare Abhängigkeiten vorliegen.

In der Praxis spielt Unabhängigkeit eine zentrale Rolle, da viele statistische Methoden und Modelle auf der Annahme beruhen, dass Zufallsvariablen unabhängig voneinander sind.

Die Unabhängigkeit zwischen Variablen wirkt sich auf die Form der Kovarianzmatrix \(\Sigma\) aus. Seien drei Zufallsvariablen \(X, Y\) und \(Z\) gegeben, die voneinander unabhängig sind. Die Kovarianzmatrix \(\Sigma\) nimmt dann die folgende, besondere Form an:

\[\begin{equation*} \Sigma = \begin{pmatrix} \sigma_x^2 & 0 & 0 \\ 0 & \sigma_y^2 & 0 \\ 0 & 0 & \sigma_z^2 \end{pmatrix} \end{equation*}\]

Alle Elemente abseits der Hauptdiagonalen, also alle Kovarianzen, sind null.

Beispiel 12.12 Sei eine normalverteilte Stichprobe von Körpergrößen mit \(N = 3\) gegeben. Die Stichprobe ist aus einer Verteilung mit \(\mu = 178\) und \(\sigma = 6\) gezogen worden (Populationswerte). Dann wird die Stichprobe \(X\) folgendermaßen dargestellt:

\[\begin{equation*} X = \begin{pmatrix} X_1 \\ X_2 \\ X_3 \end{pmatrix} \sim \mathcal{N}(\mu = 178, \Sigma), \quad \Sigma = \begin{pmatrix} \sigma^2 & 0 & 0 \\ 0 & \sigma^2 & 0 \\ 0 & 0 & \sigma^2 \end{pmatrix} \end{equation*}\]

Die Variablen \(X_i, i=1,2,3\) sind somit unabhängig und gleichverteilt (im Englischen independent identical distributed (IID)).

Mittels der Kovarianz können nun auch Varianzen von Variablen berechnet werden, wenn die beteiligten Variablen nicht mehr unabhängig voneinander sind. Es gilt für die Zufallsvariablen \(X\) und \(Y\):

\[\begin{align*} \text{Var}(aX + bY) = a^2 \text{Var}(X) + b^2 \text{Var}(Y) + 2ab \text{Cov}(X,Y) \end{align*}\]

Im Fall der Unabhängigkeit von \(X\) und \(Y\) vereinfacht sich die Rechenregel auf den oben beschriebenen Fall.

Die Unabhängigkeit ist im weiteren Verlauf zentral, da sie eine der Voraussetzungen für die Inferenz im Rahmen der einfachen und multiplen Regressionsanalyse ist. Im späteren Verlauf wird diese Annahme jedoch wieder gelockert.

12.5 Schätzer

Schätzer sind bereits in verschiedenen Varianten verwendet worden. Ein Schätzer ist eine Funktion, mit deren Hilfe anhand einer Stichprobe ein Wert, ein Schätzwert, berechnet wird. Der Schätzwert ermöglicht Rückschlüsse über unbekannte Parameter \(\phi\) in der Population. D.h. es sei zum Beispiel eine Population mit den Parametern \(\mu\) und \(\sigma^2\) gegeben, und es soll anhand der beobachteten Werte der Stichprobe eine Aussage über die Werte der beiden Parameter gemacht werden. Dazu kann ein Schätzer verwendet werden.

12.5.1 Schätzer

Ein Schätzer oder eine Schätzfunktion ist eine Statistik auf einer Stichprobe, die dazu verwendet wird, Informationen über unbekannte Parameter einer Population zu erhalten. Ein Schätzer \(t\) für den Parameter \(\theta\) (beliebiger Parameter) aus der Population wird oft mit einem Hut gekennzeichnet: \(t = \hat{\theta}\). Da \(t\) mittels der Stichprobe \(X_i, i = 1, \ldots, n\) ermittelt wird, kann manchmal auch die Schreibweise \(t = h(X_1, \ldots, X_n)\) verwendet werden, wobei \(h()\) eine Funktion (z.B. der Mittelwert) auf der Stichprobe ist.

Beispielsweise ist der Mittelwert einer Stichprobe \(\bar{x}\) ein Schätzer für den Mittelwert \(\mu\) in der Population. Die Standardabweichung \(s\) der Stichprobe ist ein Schätzer für die Standardabweichung \(\sigma\) in der Population: \(s = \hat{\sigma}\).

Es gibt jedoch eine Vielzahl möglicher Schätzer für eine gegebene Stichprobe. Zum Beispiel, wenn eine Aussage über einen Populationsmittelwert \(\mu\) getroffen werden soll, könnte der Mittelwert der drei kleinsten Werte \(\bar{x}_{123}\) anstelle des Mittelwerts über alle Stichprobenwerte \(\bar{x}\) verwendet werden. Oder der Mittelwert könnte über jeden zweiten Wert \(\bar{x}_{1,3,...n}\) berechnet werden. In diesem Fall wären drei verschiedene Schätzer für den Populationsmittelwert \(\mu\) definiert:

\[\begin{align*} \bar{x}_{123} &\rightarrow \hat{\mu} \\ \bar{x} &\rightarrow \hat{\mu} \\ \bar{x}_{1,3,...n} &\rightarrow \hat{\mu} \end{align*}\]

Allerdings sind nicht alle Schätzer gleich gut. Das Konzept des Schätzers erlaubt es, Unterschiede zwischen verschiedenen Schätzern zu formalisieren. Eine wichtige Eigenschaft von Schätzern ist die sogenannte Erwartungstreue. Die Erwartungstreue ist eng mit dem Erwartungswert einer Statistik verknüpft. Wir hatten oben gesehen, dass für den Erwartungswert des Mittelwerts \(E[\bar{x}] = \mu\) gilt. Dies zeigt, dass der Mittelwert der Stichprobe ein erwartungstreuer Schätzer für den Populationsparameter \(\mu\) ist. Im Englischen wird die Erwartungstreue als unbiased bezeichnet.

12.5.2 Bias

Der Bias ist definiert als die Abweichung zwischen dem Erwartungswert \(\hat{\theta}_{t}\) eines Schätzers \(t\) vom wahren Wert \(\theta\) in der Population.

\[\begin{equation} \text{bias}(\hat{\theta}_t) = E[\hat{\theta}_t - \theta] \label{eq-stats-hypo-bias} \end{equation}\]

Der Bias wird auch als systematischer Fehler bezeichnet.

Der Einfluss der Wahl eines Schätzers kann anhand des Beispiels mit den drei Schätzern mittels einer Simulation in R verdeutlicht werden. Sei die Population eine Standardnormalverteilung aus der Stichproben der Größe \(N = 10\) gezogen werden. Der wahre Populationsparameter ist somit \(\mu = 0\).

n_sim <- 1000
n <- 10
mu <- 0
schaetzer <- function() {
  stich <- rnorm(n, mu)
  x_123 <- mean(sort(stich)[1:3])
  x_bar <- mean(stich)
  x_13n <- mean(stich[seq(1,10,2)])
  c(x_123, x_bar, x_13n)
}
x_bar_s <- replicate(n_sim, schaetzer())

hist(x_bar_s[1,], xlim=c(-2, 2), breaks=13)
hist(x_bar_s[2,], xlim=c(-2, 2), breaks=13)
hist(x_bar_s[3,], xlim=c(-2, 2), breaks=13)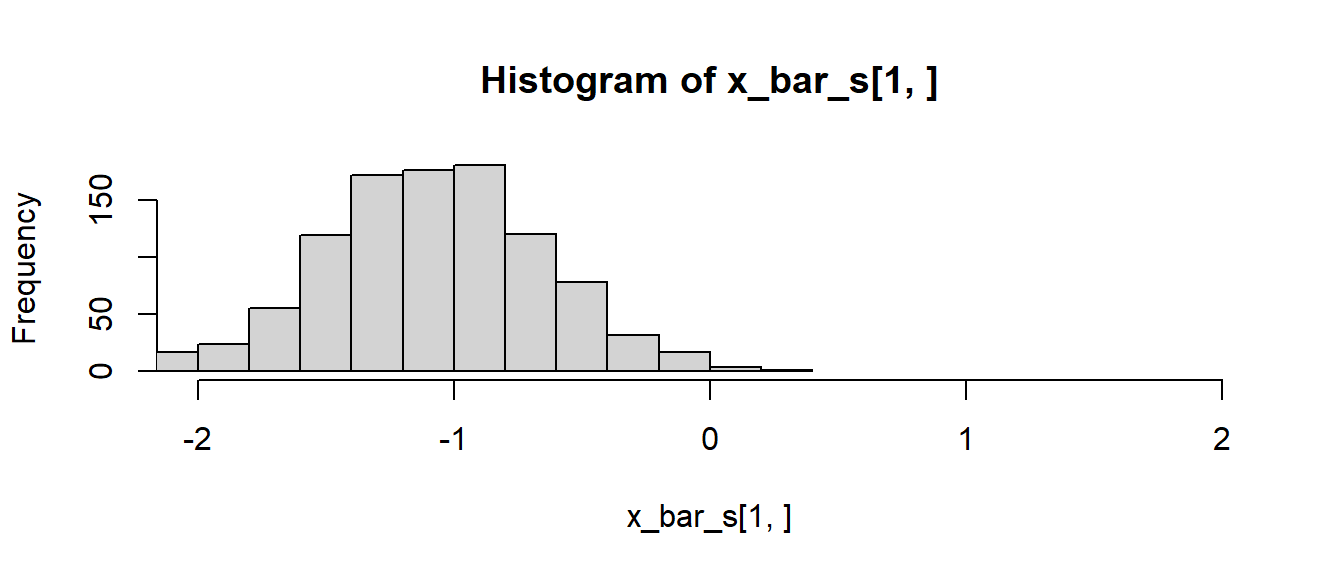

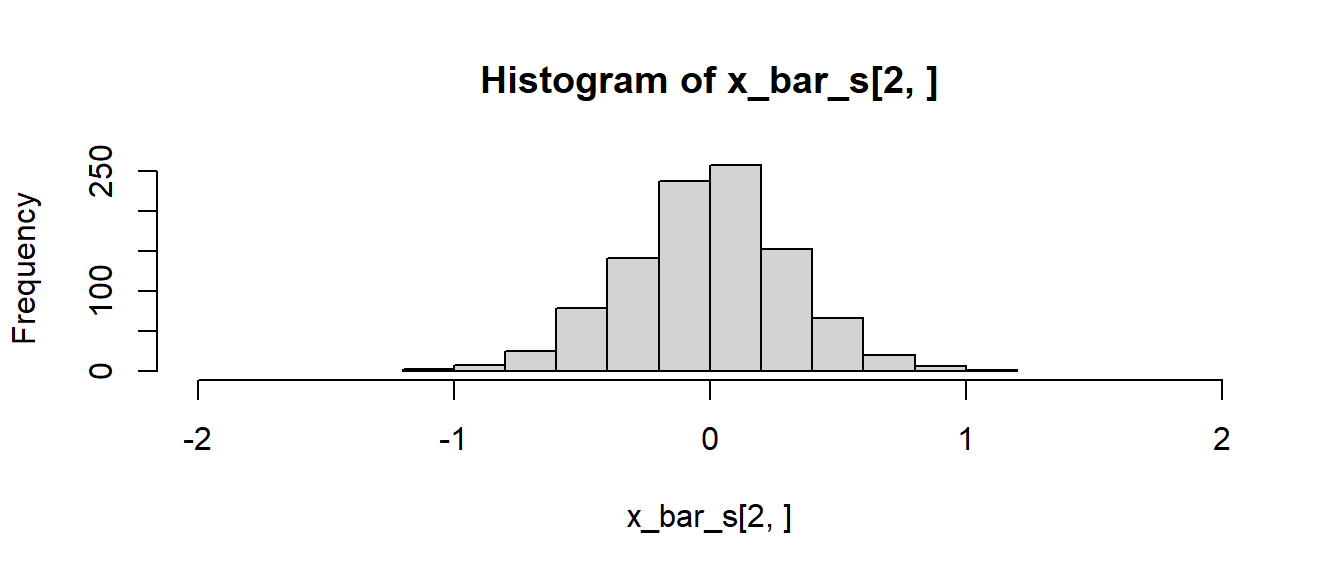
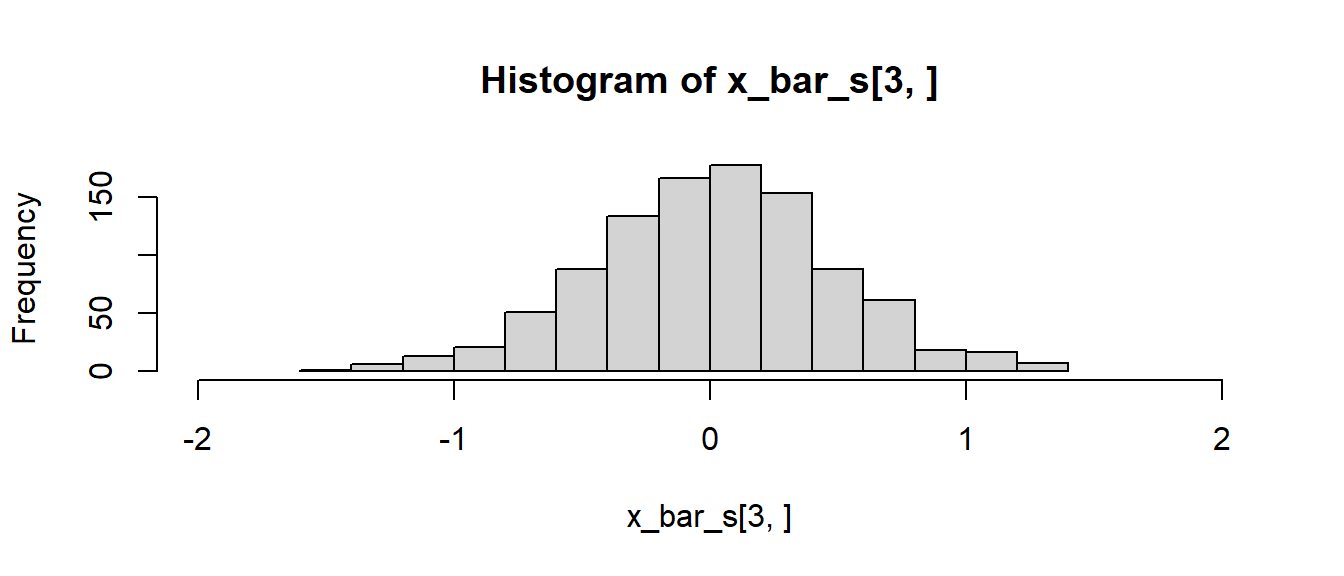
In Abbildung 12.1 ist zu erkennen, dass der Schätzer \(\bar{x}_{123}\) im Gegensatz zu den anderen beidern Schätzern nicht erwartungstreu ist. D.h. \(\bar{x}_{123}\) ist biased. Der Mittelwert der Werte ist nicht auf den tatsächlichen Populationsmittelwert \(\mu=0\) zentriert. Die beiden anderen Schätzer \(\bar{x}\) und \(\bar{x}_{1,3,...n}\) sind dagegen auf null zentriert. Daher sind diese beiden Schätzer erwartungstreu. Anwendung von Formel \(\eqref{eq-stats-hypo-bias}\) führt zu:

apply(x_bar_s, 1, mean) - mu

[1] -1.077519804 -0.003238951  0.015780503

Wird die Streuung der Histogramme betrachtet, dann ist weiterhin zu erkennen, dass der Schätzer \(\bar{x}\) eine geringere Streuung als \(\bar{x}_{1,3,...n}\) aufweist. Die Standardabweichung von \(\bar{x}\) und somit der Standardfehler ist geringer als die von \(\bar{x}_{1,3,...n}\). Generell versucht man, Schätzer zu finden, die möglichst wenig streuen bzw. optimal im Sinne ihrer Varianz sind. Das bedeutet, Schätzer, deren Standardfehler möglichst klein ist, damit der Schätzer möglichst wenig um den tatsächlichen Populationswert streut.

Zum gleichen Ergebnis kommt eine formale Herleitung der Varianzen der beiden Schätzer \(\bar{X}\) und \(\bar{X}_{1,3,...n}\). Es wurde vorher bereits gezeigt, dass der Standardfehler des Mittelwerts den bekannten Wert \(\frac{\sigma}{\sqrt{n}}\) hat. Da der Schätzer \(\bar{X}_{1,3,...n}\) nur die halbe Stichprobe verwendet, ergibt sich anhand der gleichen Herleitung der Standardfehler \(\frac{\sigma}{\sqrt{n/2}} = \frac{\sigma\sqrt{2}}{\sqrt{n}}\). Das bedeutet, der Standardfehler des Schätzers \(\bar{x}_{1,3,...n}\) ist um den Faktor \(\sqrt{2}\) größer als derjenige von \(\bar{x}\).

s_es <- apply(x_bar_s, 1, sd)
s_es

[1] 0.4279019 0.3227427 0.4644991

s_es[2]*sqrt(2)

[1] 0.4564271

Auch hier ist zu erkennen, dass im Rahmen der Stichprobenvariabilität der korrekte Wert erhalten wird.

Beispiel 12.13 (Erwartungstreue von \(s\)) Eine häufig gestellte Frage in der Statistikvorlesung betrifft den Divisor \(n-1\) bei der Berechnung der Standardabweichung in der Stichprobe. Mit \(\sigma^2 = E[X^2] - E[X]^2 = E[X^2] - \mu^2 \Rightarrow E[X^2] = \sigma^2 + \mu^2\) und den Rechenregeln für den Erwartungswert können wir zeigen, warum die Standardabweichung \(s\) bzw. die Varianz \(s^2\) einer Stichprobe als Schätzer für \(\sigma\) bzw. \(\sigma^2\) geeignet ist, also \(s = \hat{\sigma}\) bzw. \(s^2 = \hat{\sigma}^2\).

\[\begin{equation} s^2 = \frac{\sum_{i=1}^n (x_i - \bar{x})^2}{n-1} \end{equation}\]

Es folgt:

\[\begin{align*} E\left[\sum_{i=1}^{n} (x_i-\bar x)^2\right] &= E[\sum_{i=1}^{n} x_i^2-2\bar x\sum_{i=1}^{n} x_i+n\bar{x}^2]\\ &=E[\sum_{i=1}^{n} x_i^2-2\bar{x}n\bar{x}+n\bar{x}^2]\\ &= E[\sum_{i=1}^{n} x_i^2-n\bar{x}^2] \\ &= n E[x_i^2]- n E[\bar{x}^2]\\ &= n (\mu^2 + \sigma^2) - n(\mu^2+\sigma^2/n)\\ &= (n-1) \sigma^2 \end{align*}\]

Daraus folgt:

\[\begin{equation*} E[s^2] = E\left[\frac{\sum_{i=1}^n (x_i - \bar{x})^2}{n-1}\right] = \sigma^2 \end{equation*}\]

Das erklärt, warum die Summe der quadrierten Abweichungen durch \(n-1\) und nicht durch \(n\) geteilt wird.

Würden die quadrierten Abweichungen durch \(n\) geteilt, dann hätten wir keinen erwartungstreuen Schätzer mehr:

\[\begin{equation*} E\left[\frac{\sum_{i=1}^n (x_i - \bar{x})^2}{n}\right] = \frac{1}{n}E\left[\sum_{i=1}^n (x_i - \bar{x})^2\right] = \frac{n-1}{n}\sigma^2 \end{equation*}\]

Würde durch \(n\) geteilt, würde die Varianz unterschätzt, da \(\frac{n-1}{n}<1\) gilt. In diesem Fall hätte der Schätzer einen Bias (systematischen Fehler).

Zusammenfassend benötigt man möglichst erwartungstreue Schätzer, um eine verlässliche Verbindung zwischen einer Stichprobe und den Parametern einer theoretischen Verteilung herzustellen.

12.6 Hypothesentestungszoo

Es folgt eine kurze Übersicht über verschiedene Teststatistiken, die im weiteren Verlauf des Skripts immer wieder auftauchen werden.

12.6.1 Der t-Test

Wir hatten bereits gesehen, dass das Verhältnis einer standardnormalverteilten Variablen zu einer \(\chi^2\)-verteilten Variablen einer \(t\)-Verteilung folgt. In vielen Fällen wird diese Eigenschaft verwendet, wenn ein Unterschied \(\hat{\Delta}\), beispielsweise zwischen zwei Mittelwerten \(\bar{x} - \bar{y}\), durch eine Streuung \(\hat{s}_e(\hat{\Delta})\) geteilt wird:

\[\begin{equation*} T = \frac{\hat{\Delta}}{\hat{s}_e(\hat{\Delta})} \sim t\text{-Verteilung} \end{equation*}\]

Zum Beispiel wird beim t-Test, der uns in unserer ersten Statistikvorlesung begegnet ist, der Unterschied zwischen zwei Gruppenmittelwerten durch den Standardfehler der Differenz geteilt.

12.6.2 \(\chi^2\)-Test der Varianz

Die \(\chi^2\)-Verteilung tritt häufig im Zusammenhang mit Schätzern von Varianzen auf. Beispielsweise lässt sich zeigen, dass bei \(n\) unabhängigen, standardnormalverteilten Variablen \(X_i, i = 1, \ldots, n\), die Summe der quadrierten Abweichungen vom Mittelwert, also \(\sum_{i=1}^n(Y_i - \bar{Y})^2\), einer \(\chi^2\)-Verteilung mit \(n-1\) Freiheitsgraden folgt.

Sei \(\hat{\sigma}^2\) ein Schätzer für die Varianz aus einer Stichprobe und es soll überprüft werden, ob diese Varianz einer vorgegebenen Varianz \(\sigma_0^2\) entspricht, also \(H_0: \sigma^2 = \sigma_0^2\) die Nullhypothese ist. Dann lässt sich eine Teststatistik \(T\) über die folgende Formel konstruieren:

\[\begin{equation*} T = d \frac{\hat{\sigma}^2}{\sigma_0^2} \sim \chi^2 \quad d = \text{Freiheitsgrade} \end{equation*}\]

\(H_0\) wird dann abgelehnt, wenn \(T > q_{\chi^2,\text{df}=d,1-\alpha}\) (einseitig) gilt.

12.6.3 F-Test von Varianzverhältnissen

Sei eine Stichprobe aus normalverteilten, unabhängigen Variablen gegeben, und seien die Varianzen \(\sigma_A^2\) und \(\sigma_B^2\) mittels zweier Schätzer \(\hat{\sigma}_A^2\) und \(\hat{\sigma}_B^2\) bestimmt worden. Dann kann eine Teststatistik \(T\) konstruiert werden, um die Gleichheit der beiden Varianzen zu überprüfen. Formal lautet die Nullhypothese \(H_0: \sigma_A^2 = \sigma_B^2 \Leftrightarrow \frac{\sigma_A}{\sigma_B} = 1\).

\[ T = \frac{\hat{\sigma}^2_A}{\hat{\sigma}^2_B} \sim F(df_A, df_B) \]

Die beiden Varianzen folgen jeweils einer \(\chi^2\)-Verteilung mit Freiheitsgraden \(df_A\) und \(df_B\). Daher folgt die Statistik \(T\) unter \(H_0\) einer \(F\)-Verteilung mit \((df_A, df_B)\) Freiheitsgraden. Die Nullhypothese \(H_0\) wird wiederum abgelehnt, wenn \(T > q_{F,\text{df}_A,\text{df}_B, 1-\alpha}\) (einseitig) gilt.

12.6.4 Zusammenfassung

Wie bereits bei der Auflistung der theoretischen Verteilungen erwähnt, ist es zunächst wichtig, zur Kenntnis zu nehmen, dass es diese unterschiedlichen Tests gibt. Deren Herleitung ist mit den bisher gegebenen Informationen nicht vollständig nachvollziehbar und bleibt oft abstrakt. Die Liste ist daher eher im Sinne einer Mustererkennungsaufgabe für später zu verstehen. Wenn die Tests im weiteren Verlauf des Skripts in konkreten Zusammenhängen auftauchen, sollte ein Wiedererkennungswert entstehen.

Letztendlich bleibt das anzuwendende Prinzip immer gleich:

Teststatistik berechnen
Theoretische Verteilung bestimmen
Kritischen Wert unter \(H_0\) über das Quantil \(\alpha\) finden
Testentscheidung und Unsicherheit beurteilen.

Was sich ändert, sind die Tests und deren spezifische Parameter.