23 Logistische Regression
In der bishergen Behandlung der Regression war die Kriteriumsvariable, also die abhängige Variable, immer eine metrische Variable deren Wertebereich im Prinzip von \(-\infty\) bis \(\infty\) ging. In der Realität ist dies natürlich nicht tatsächlich der Fall, da beispielsweise die Wurfgeschwindigkeit im Handball in der Realität durch die physiologische Kapazität der Spieler:Innen beschränkt ist. Allerdings gibt es auch den Fall, dass die Kriteriumsvariable überhaupt nur Werte innerhalb eines bestimmten Intervalls zulässt. Die Wahrscheinlichkeit ein Tor im Handball zu werfen beispielsweise kann nur Werte im Intervall \([0,1]\) einnehmen. Soll nun Beispielsweise ein Regressionsmodell erstellt werden um die Torwahrscheinlichkeit \(p_{\text{Tor}}\) beispielsweise anhand des Abstands \(d\) zum Tor und des Winkels \(\alpha\) von der Torfläche vorherzusagen, dann kann dies im Prinzip mit einem multiplen Regressionmodell durchgeführt werden.
\[ p_{\text{Tor},i} = \beta_0 + \beta_1 d_i + \beta_2 \alpha_i + \epsilon_i \]
Allerdings verhindert nichts, dass \(p_{\text{Tor},i}\) Werte außerhalb des Bereichs \([0,1]\) einnehmen kann. D.h. um die Idee eines linearen Regressionsmodells auf dieses Problem auszuweiten ist eine Beschränkung der möglichen Werte notwendig.
Eine weitere Besonderheit im Zusammenhang mit dem Handballbeispiel, hängt mit Eigenschaft zusammen, dass die Werte der abhängigen Variable \(Y\) in der Realität nur zwei Werte einehmen können. Mit der Zuweisung \(\text{Tor} = 1\) und \(\text{Fehlversuch} = 1\) nimmt \(Y\) immer nur die Werte \(0\) oder \(1\) ein. Entsprechend würde ein Datensatz die folgende Form haben:
| Tor | Abstand[m] | Winkel[°] |
|---|---|---|
| 0 | 4 | 45 |
| 1 | 5 | 90 |
| 0 | 3.5 | 30 |
Unter diesem Aspekt, kann dieses Problem auch als Klassifikationsproblem interpretiert werden. Es sind zwei verschiedene Klassen vorhanden, Tor und kein Tor und es soll anhand bestimmter Prädiktorvariablen vorhergesagt werden, zu welcher Klasse ein Objekt zugeordnet werden kann. Ähnliche Problemstellung ergeben sich auch im medizinischen Kontext, wo beispielsweise anhand einer Reihe von Prädiktorvariablen bestimmt werden soll, ob ein:e Patient:In erkrankt oder gesund bleibt.
Die Lösung für diese beiden Problem bietet die Logistische Regression die im Folgenden behandelt wird. Glücklicherweise können die meisten bereits gelernten Konzepte auch im Kontext der logistischen Regression angewendet werden und alles was es braucht ist ein zusätzlicher Kniff um die Beschränkung des Wertebereichs zu erreichen. Zusätzlich kommt noch ein komplett neuer Aspekt hinzu, da die logistische Regression eben auch als die Lösung für ein Klassifikationsproblem interpretiert werden kann. Dadurch ergibt sich eine enge Anbindung an den Bereich des Maschinellen Lernens in die Klassifikationsalgorithm eine zentrale Rolle spielen.
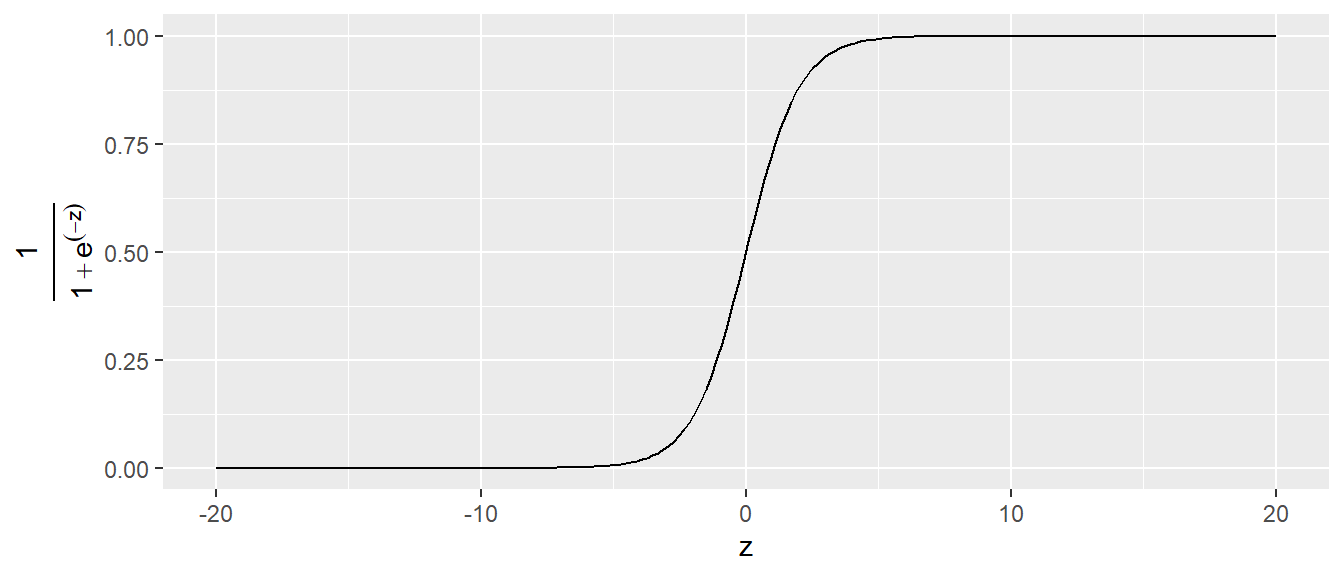
23.1 Logistische Funktion
\[ f(z) = \frac{1}{1 + e^{-z}} \]
23.2 Alternative Formulierung der logistischen Funktion
\[\begin{align*} f(z) &= \frac{1}{1 + e^{-z}} \\ &= \frac{e^z}{e^z + e^{-z}e^z} \\ &= \frac{e^z}{e^z + e^{-z+z}} \\ &= \frac{e^z}{e^z + 1} \end{align*}\]
23.3 logistic function \(f(z,a) = \frac{1}{1+e^{-az}}\)
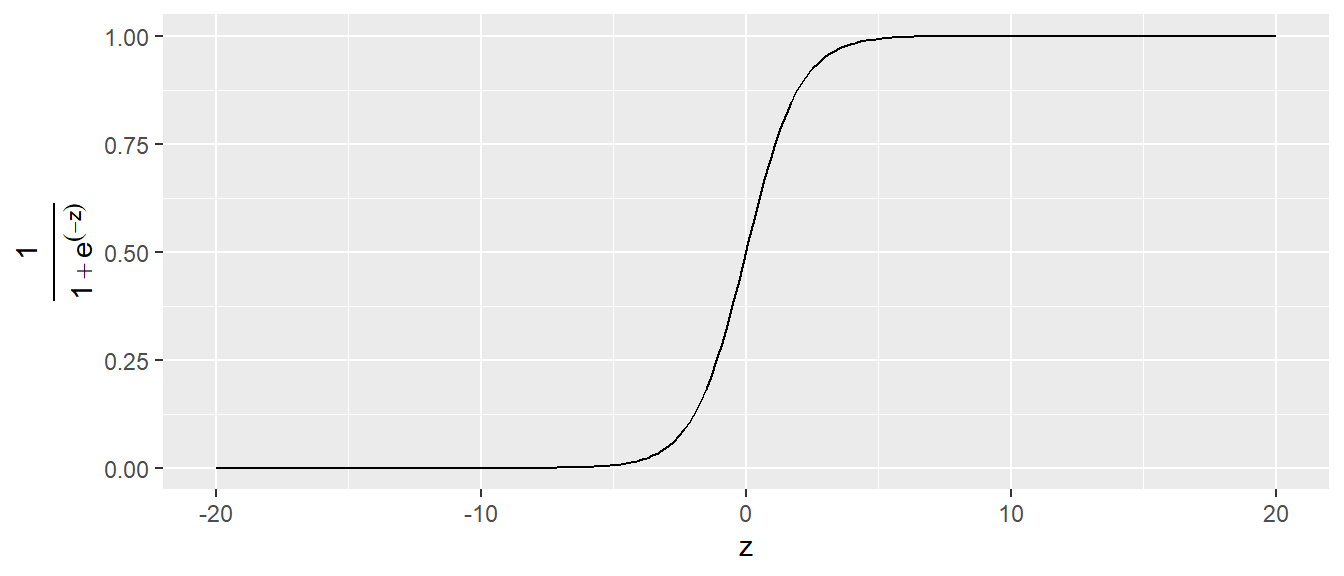
23.4 Logistic function to model probabilities
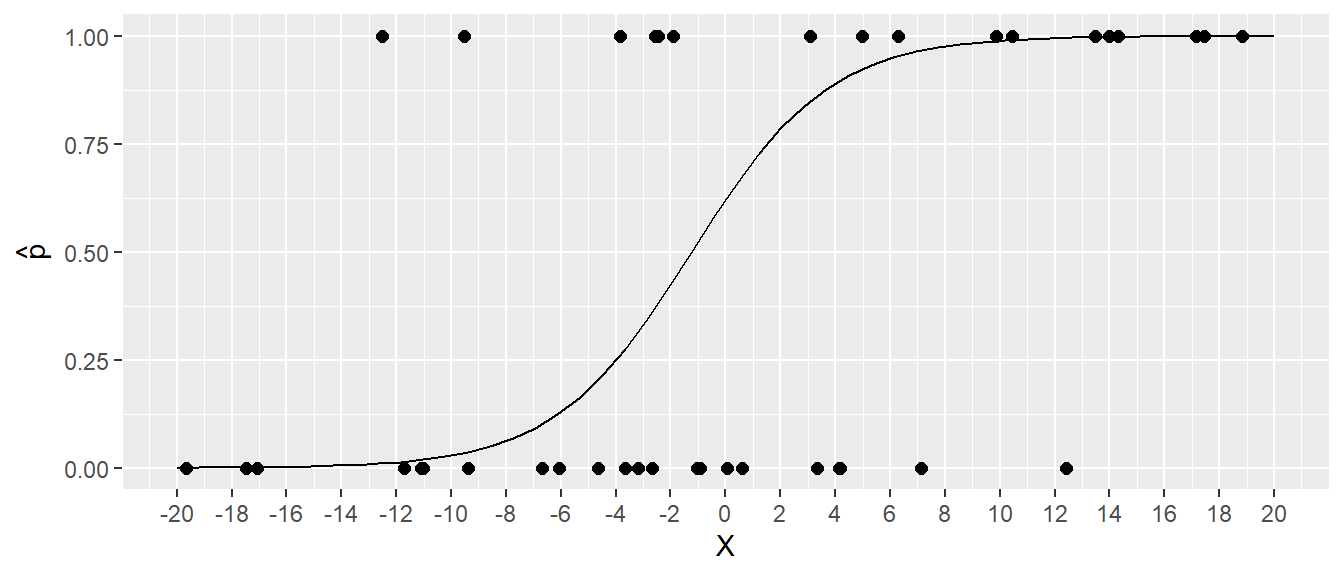
\[\begin{align*} p(X) = f(\beta_0 + \beta_1 X) &= \frac{e^{\beta_0+\beta_1 X}}{1 + e^{\beta_0 + \beta_1 X}} \\ &= \frac{1}{1+e^{-(\beta_0 + \beta_1 X)}} \end{align*}\]
\(p(X)\) as the probability of scoring a goal, or the risk of developing a disease, etc.
\[ P(Y = 1|X) = \frac{1}{1 + e^{-(\beta_0 + \beta_1 X)}} \]
23.5 Logistische Regression in R
23.6 Vorhersage
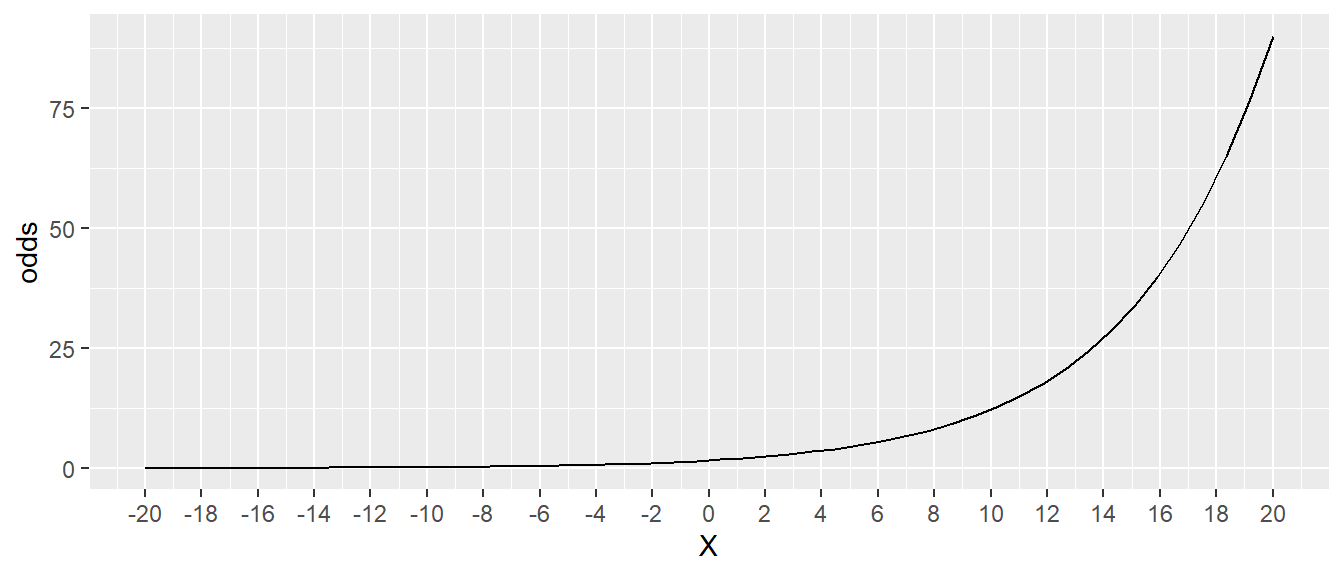
23.7 Chance

\[\begin{align*} \text{odds} &= \frac{P(\text{Event})}{P(\text{Not Event})} \\ &= \frac{p}{1-p} \\ \end{align*}\]
23.8 odds and the logistic model
\[\begin{align*} p(X) &= \frac{e^{\beta_0 + \beta_1X}}{1 + e^{\beta_0 + \beta_1 X}} \\ \Leftrightarrow p(X)(1 + e^{\beta_0 + \beta_1 X}) &= e^{\beta_0 + \beta_1X} \\ \Leftrightarrow p(X) + p(X)e^{\beta_0 + \beta_1 X} &= e^{\beta_0 + \beta_1X} \\ \Leftrightarrow p(X) &= e^{\beta_0 + \beta_1X} - p(X)e^{\beta_0 + \beta_1 X} \\ \Leftrightarrow p(X) &= e^{\beta_0 + \beta_1X}(1 - p(X)) \\ \Leftrightarrow \frac{p(X)}{1 - p(X)} &= e^{\beta_0 + \beta_1X} \\ \end{align*}\]
23.9 Logit function
\[ \text{logit}(x) = \text{log}\left(\frac{x}{1-x}\right) \]
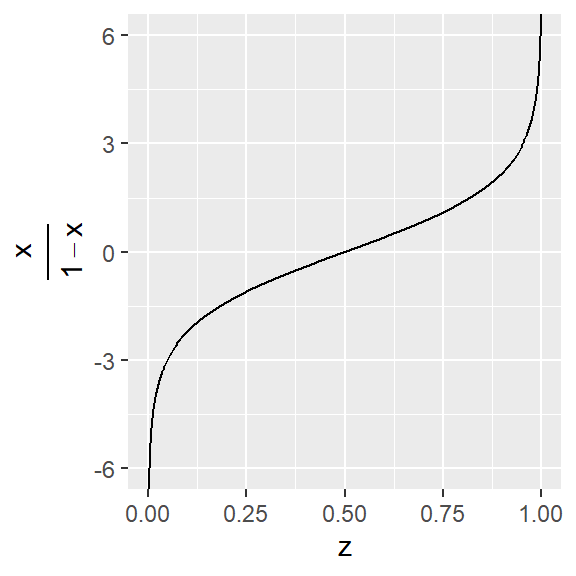
23.10 log-odds or logit
\[ \text{logit}\left(\frac{p(X)}{1-p(X)} \right) = \beta_0 + \beta_1 X \]
The logistic regression model is linear for \(X\) in the log-odds. \[\begin{align*} \left(\frac{p(X)}{1-p(X)} \right) &= e^{\beta_0 + \beta_1 (X + \Delta)} = e^{\beta_0 + \beta_1X}e^{\beta_1 \Delta} \\ log\left(\frac{p(X)}{1-p(X)} \right) &= log\left(e^{\beta_0 + \beta_1X}e^{\beta_1\Delta}\right) = \beta_0 + \beta_1 X + \beta_1 \Delta \end{align*}\]
23.11 Changes in \(Y\) according to \(X\)
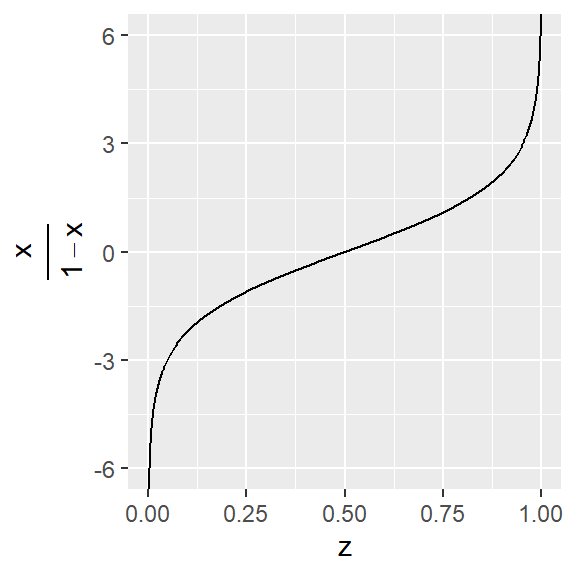
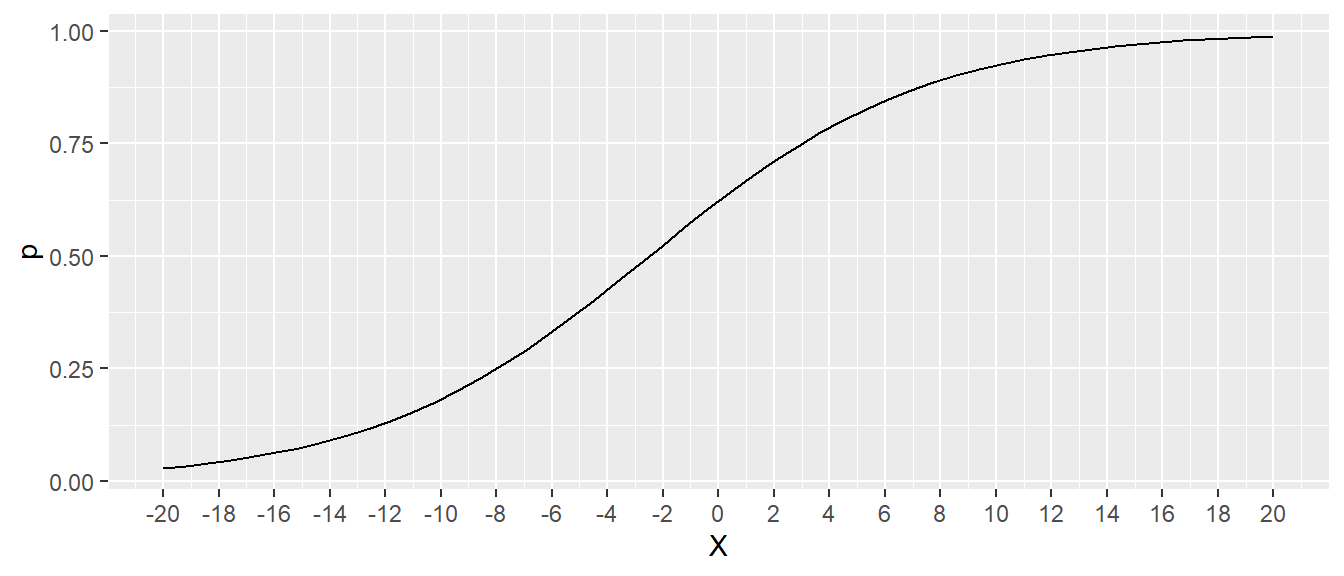
\(f(x) = \frac{e^{0.5+0.2x}}{1+e^{0.5+0.2x}}\)
23.12 Konfusionsmatrize
| Predicted: Positive | Predicted: Negative | |
|---|---|---|
| Actual: Positive | True Positive (TP) | False Negative (FN) |
| Actual: Negative | False Positive (FP) | True Negative (TN) |
- Accuracy: \((TP + TN) / \text{Total Samples}\)
- Precision (Positive Predictive Value): \(TP / (TP + FP)\)
- Recall (Sensitivity): \(TP / (TP + FN)\)
- F1 Score: \(\frac{2}{\frac{1}{\text{Precision}} + \frac{1}{\text{Sensitivity}}} \in [0,1]\)
23.13 Welche Eigenschaften sind wichtig für einen Klassifikationsalgorithmus?
- Discrimination
- Calibration
23.14 Discrimination
23.14.1 Definition
Discrimination refers to a model’s ability to distinguish between positive and negative cases. Discrimination assesses how well a model separates different outcome classes.
Intuition: Discrimination tells us how well the model differentiates between classes, regardless of the predicted probability values being perfectly aligned with real-world outcomes.
23.15 Kalibrierung
23.15.1 Definition:
Calibration refers to the agreement between predicted probabilities and the observed proportions of outcomes. A well-calibrated model outputs probabilities that reflect the true likelihood of an event.
Intuition: Calibration ensures that the model’s predictions are not just accurate in classification but also reliable as probability estimates.
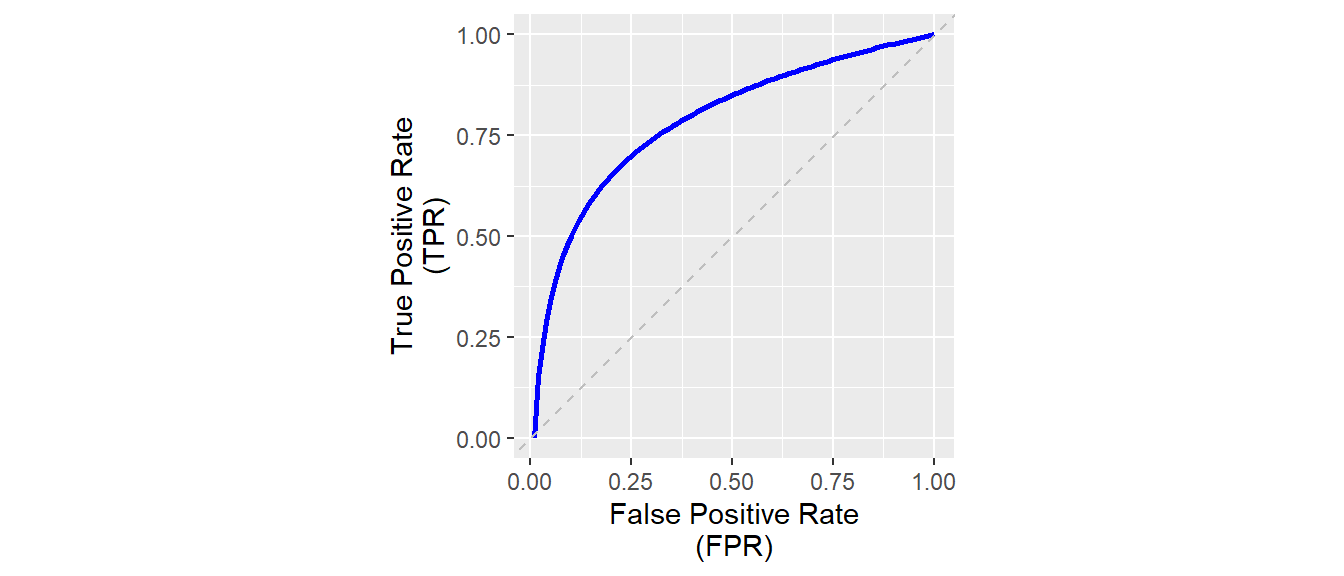
23.16 Receiver Operator Characteristic (ROC)
\[ \text{True Positive Rate (TPR, Sensitivity)} = \frac{\text{True Positives}}{\text{True Positives + False Negatives}} \]
\[ \text{False Positive Rate (FPR)} = \frac{\text{False Positives}}{\text{False Positives + True Negatives}} \]
\[ \text{Specificity} = \frac{\text{True Negatives}}{\text{True Negatives + False Positives}} \]
\[ \text{FPR} = 1 - \text{Specificity} \]
23.17 ROC
23.18 ROC curve
23.19 Area under the curve (AUC)
23.20 Calibration curve
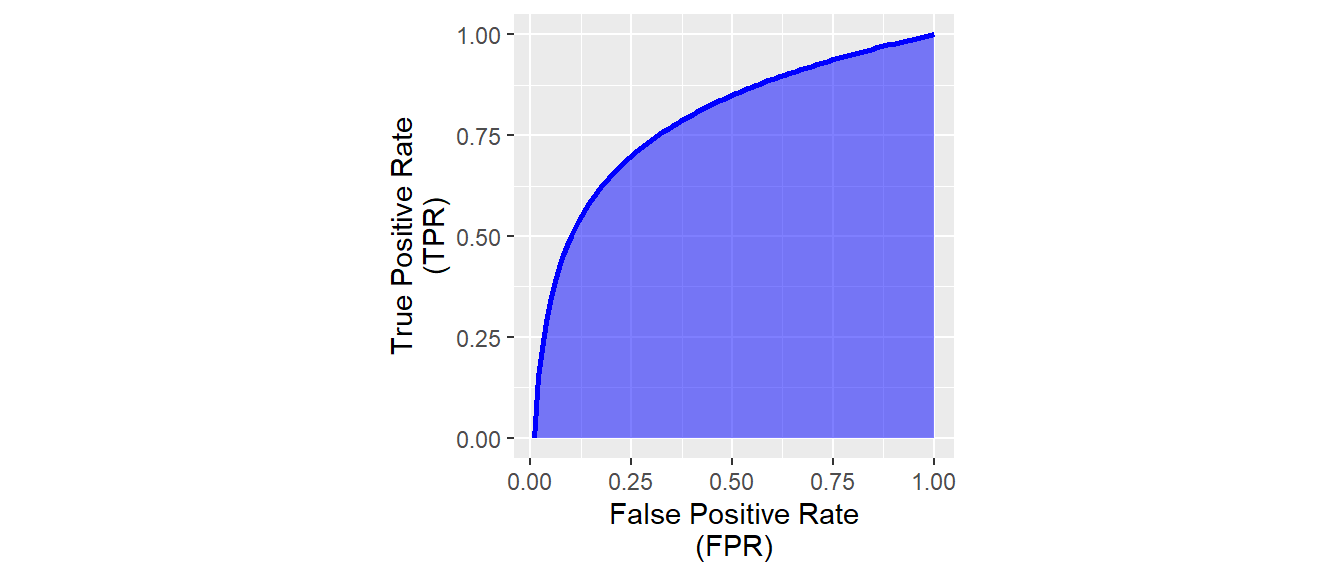
23.21 Calculating a prediction curve
23.22 CalibrationCurves
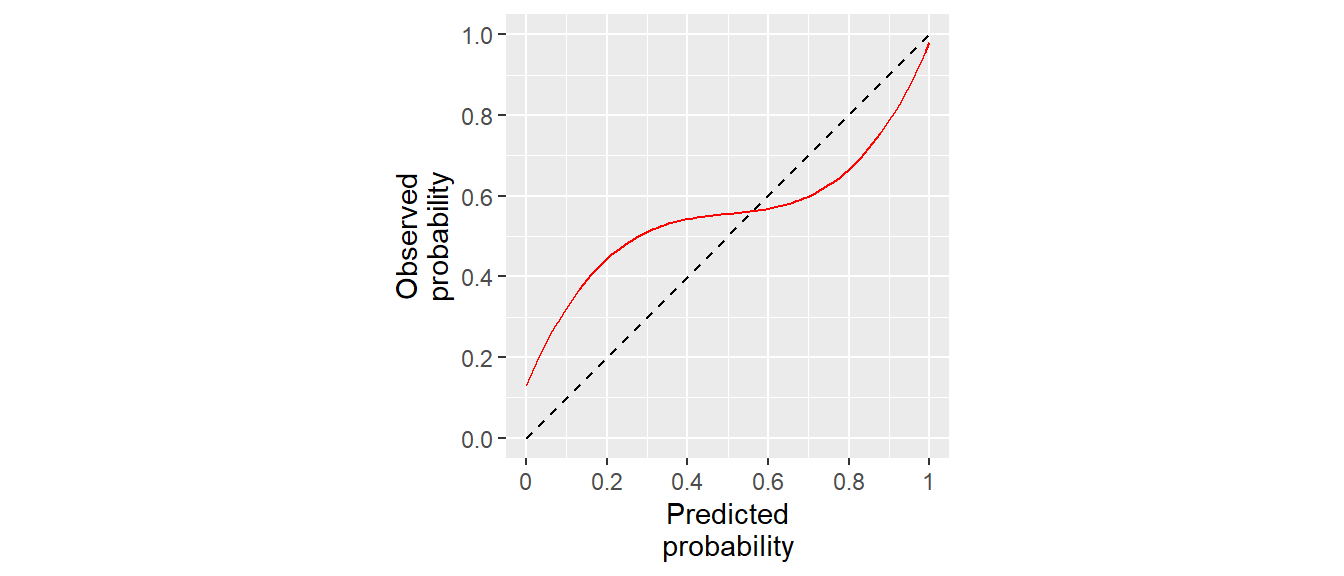
23.23 Take-aways Diskriminierung vs. Kalibrierung
| Aspect | Discrimination | Calibration |
|---|---|---|
| Focus | Ability to distinguish classes | Accuracy of predicted probabilities |
| Measurement | AUC, ROC curves | Calibration curves |
| Key Question | “How well does the model rank cases?” | “Are the probabilities realistic?” |