mod_1 <- lm(vel ~ body_mass + arm_span, handball)18 Interaktionseffekte
Bisher sind die Variablen in das multiple Regressionsmodell nur additiv eingegangen. D.h. in der Modellspezifikation sind die Prädiktorvariablen \(x_i\) immer nur mit einem \(+\) in die Formel eingegangen. Im folgenden soll nun untersucht werden, was passiert wenn die Prädiktorvariablen auch multiplikativ in das Modell eingehen. Dies führt dann zu sogenannten Interaktionseffekten.
18.1 Ein Handballbeispiel
Ausgangspunkt sei ein hypothetischen Datensatz aus dem Handball angelehnt an die Übung. Es sei ein Datensatz mit drei Datenspalten gegeben. Die Variablen sind die Wurfgeschwindigkeit, die Körpermasse und die Armspannweite. Ziel ist es, die Wurfgeschwindigkeit anhand der Körpermasse und der Armspanweite zu modellieren angelehnt an Debanne und Laffaye (2011). Zunächst, wie immer, eine Betrachtung der deskriptiven Daten (siehe Tabelle 18.1).
| Mean | Std.Dev | Min | Max | |
|---|---|---|---|---|
| Armspannweite[cm] | 184.29 | 7.72 | 169.43 | 200.74 |
| Körpermasse[kg] | 77.46 | 10.26 | 57.95 | 101.12 |
| Wurfgeschwindigkeit[m/s] | 21.85 | 2.31 | 18.50 | 29.22 |
In Tabelle 18.1 ist zunächst einmal nichts auffallendes zu sehen. Vielleicht sind die Wurfgeschwindigkeiten etwas zu niedrig für Hochleistungshandballer, aber das stört die weitere Analyse der Daten. Als nächstes erfolgt eine Betrachtung der Daten mittels von Streudiagrammen.
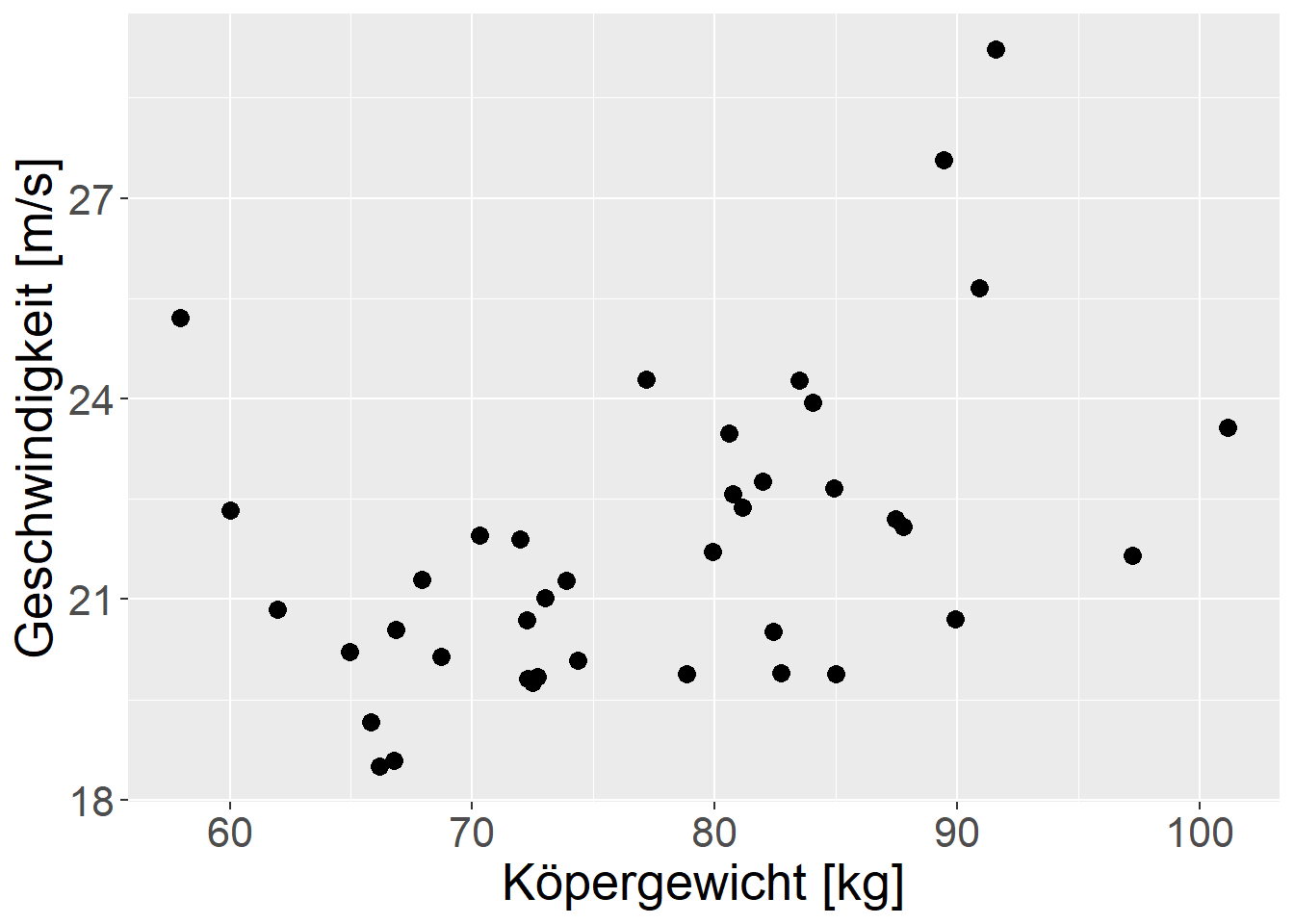
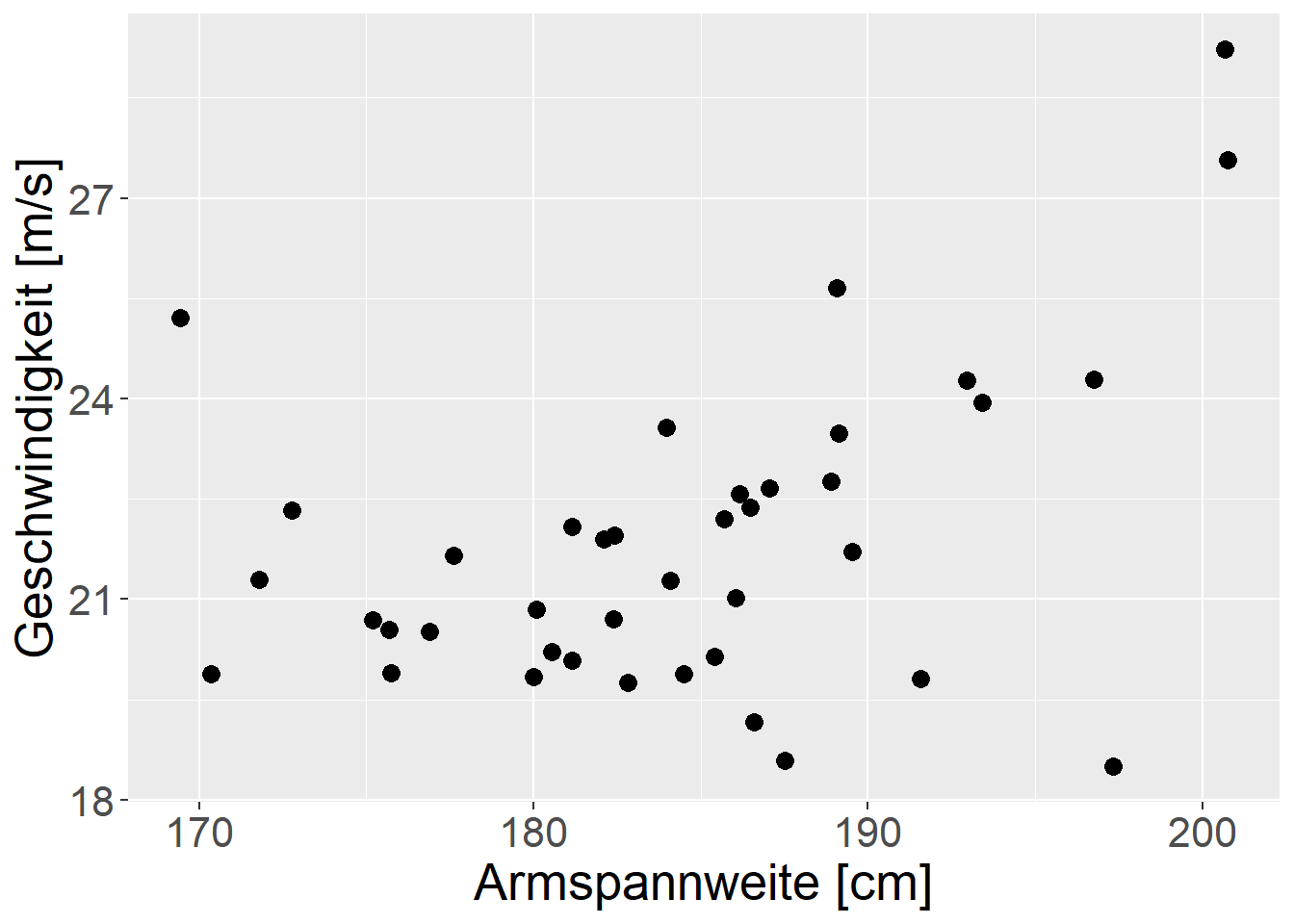
In beiden Graphen ist mit etwas gutem Willen ein positiver Zusammenhang zwischen den jeweiligen Prädiktorvariablen und der Wurfgeschwindigkeit zu identifizieren. Für das Körpergewicht in Abbildung 18.1 (a) vielleicht etwas mehr als für die Armspannweite in Abbildung 18.1 (b).
Nun sollen die Daten mittels eines linearen Modells modelliert werden.
\[\begin{equation*} Y_{i} = \beta_0 + \beta_1 \times \textrm{bm}_i + \beta_2 \times \textrm{as}_i + \epsilon_i \end{equation*}\]
Mit lm() in R Code übersetzt:
Bei Betrachtung der Modellparameter (siehe Tabelle 18.2) ist zu erkennen, dass die Steigungskoeffizienten zwar knapp statistisch signifikant sind, aber in Bezug auf die Residualvarianz bzw. den Standardfehler \(\hat{\sigma}\) eine ziemlich hohe Restunsicherheit \(\hat{\sigma} = 1.9958\) aufweisen. Dies macht die Vorhersage letztendlich unbrauchbar.
| \(\hat{\beta}\) | \(s_e\) | t | p | |
|---|---|---|---|---|
| (Intercept) | -1.768 | 7.632 | -0.232 | 0.818 |
| body_mass | 0.077 | 0.033 | 2.359 | 0.024 |
| arm_span | 0.096 | 0.044 | 2.192 | 0.035 |
| \(\hat{\sigma}\) | 1.996 |
Der \(y\)-Achsenabschnitt \(\beta_0\) im Modell macht auch ebenfalls keinen Sinn, da er, verbal übersetzt ausdrückt, dass ein Handballer mit einer Spannweite von \(0\)cm und einer Körpermasse von \(0\) Kg eine Wurfgeschwindigkeit von \(v = -1.8\)m/s erreichen würde. Um den \(y\)-Achsenabschnitt interpretierbar zu machen, ist damit wie schon so oft sinnvoll die Daten zu zentrieren. Dies ändert wieder nichts an dem Modellfit, aber der \(y\)-Achsenabschnitt bekommt dadurch einen sinnvollen Wert. Wie immer beim Zentrieren, werden von den Prädiktorvariablen die jeweiligen Mittelwert abgezogen. Übersetzt in R-Code mittels der Funktion mutate().
handball <- dplyr::mutate(handball,
body_mass_c = body_mass - mean(body_mass),
arm_span_c = arm_span - mean(arm_span))Nun wird wieder da gleiche Modell angepasst, wobei die zentrierten Variablen als Prädiktorvariablen verwendet werden.
mod_2 <- lm(vel ~ body_mass_c + arm_span_c, handball)Wie erwartet ändert dies nichts an den Modellwerten, bis auf den \(y\)-Achsenabschnitt. Der Wert von \(21.8\) ist jetzt dahingehend zu interpretieren, dass ein Handballer mit einer Armspannweite von \(184\)cm und einer Körpermasse von \(77\)Kg eine Wurfgeschwindigkeit von \(21.9\)m/s erreichen sollte (siehe Tabelle 18.1 und Tabelle 18.3).
| \(\hat{\beta}\) | \(s_e\) | t | p | |
|---|---|---|---|---|
| (Intercept) | 21.852 | 0.316 | 69.247 | <0.001 |
| body_mass_c | 0.077 | 0.033 | 2.359 | 0.024 |
| arm_span_c | 0.096 | 0.044 | 2.192 | 0.035 |
| \(\hat{\sigma}\) | 1.996 |
Nun erfolgt wie immer eine Betrachtung der Residuen \(e_i\) im zentrierten, additiven Modell (Model 2) (siehe Abbildung 18.2).
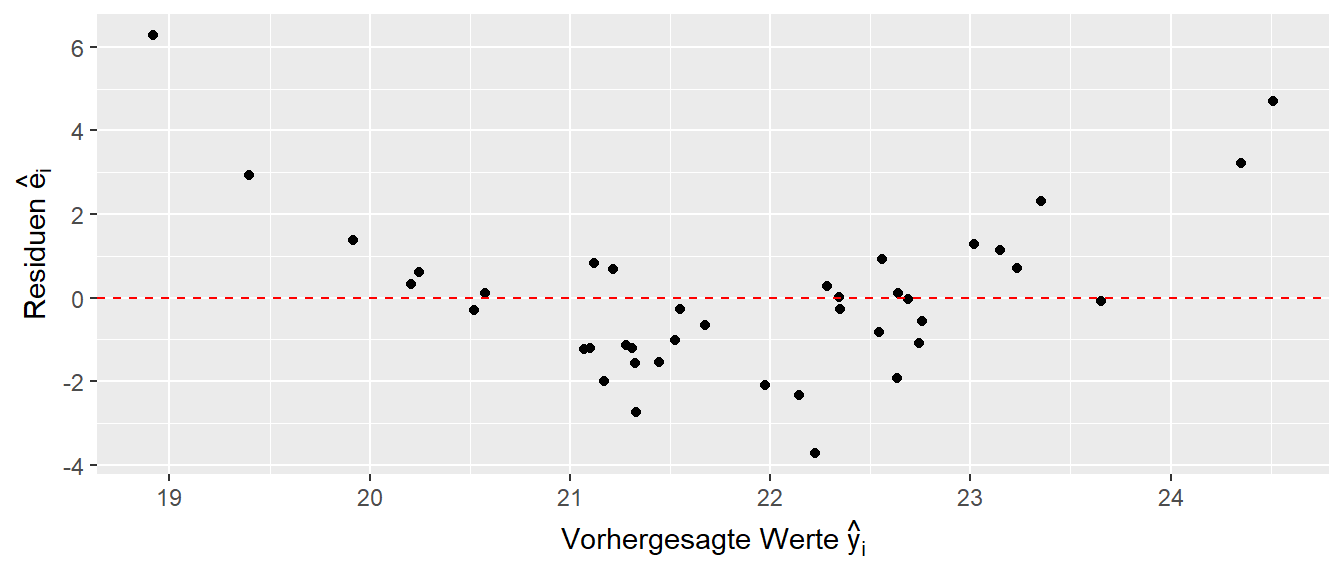
Da die Werte für kleine und große vorhergesagte Werte \(\hat{y}_i\) ganz klar ein Muster aufweisen, kann davon ausgegangen werden, das das Modell eine in den Daten vorhandene Struktur nicht zu modellieren im Stande ist. Dazu wird nun noch einmal der Einfluss der Prädiktorvariablen auf die Wurfgeschwindigkeit genauer untersucht.
Um den Zusammenhang der beiden Variablen zusammen zu untersuchen werden nun Hilfsvariablen definiert. Dazu wird eine künstliche Unterteilung der Armspannweiten und Körpermassen in drei verschiedene Kategorien vorgenommen. D.h. die Armspannweite wird in kurze, mittlere und lange Spannweiten und die Körpermasse wird in leicht, mittel und schwer unterteilt.
| arm_span_c | as_f | body_mass_c | bm_f |
|---|---|---|---|
| 1.13 | mittel | -8.75 | leicht |
| -0.21 | mittel | -3.61 | mittel |
| 16.45 | lang | 11.97 | schwer |
| -13.95 | kurz | 7.51 | schwer |
| -7.40 | kurz | 4.94 | mittel |
| 16.39 | lang | 14.11 | schwer |
In Tabelle 18.4 ist ein Ausschnitt der Daten zu sehen. Hier sind die beiden neuen Spalten die die kontinuierlichen Variablen Körpermasse und Armspannweite jeweils in eine nominale Variable abbilden abgetragen. Hier ist zu erkennen, dass größere positive Werte jeweils als lang bzw. schwer kategorisiert werden und entsprechend kleine absolute Wert als mittel und kleine negative Werte als kurz bzw. leicht. Die Geschwindigkeitsdaten können nun in einem Graphen abgebildet werden, bei dem nicht mehr die originalen, kontinuierlichen Daten, sondern nun die beiden nominalen Variablen verwendet werden (siehe Abbildung 18.3).
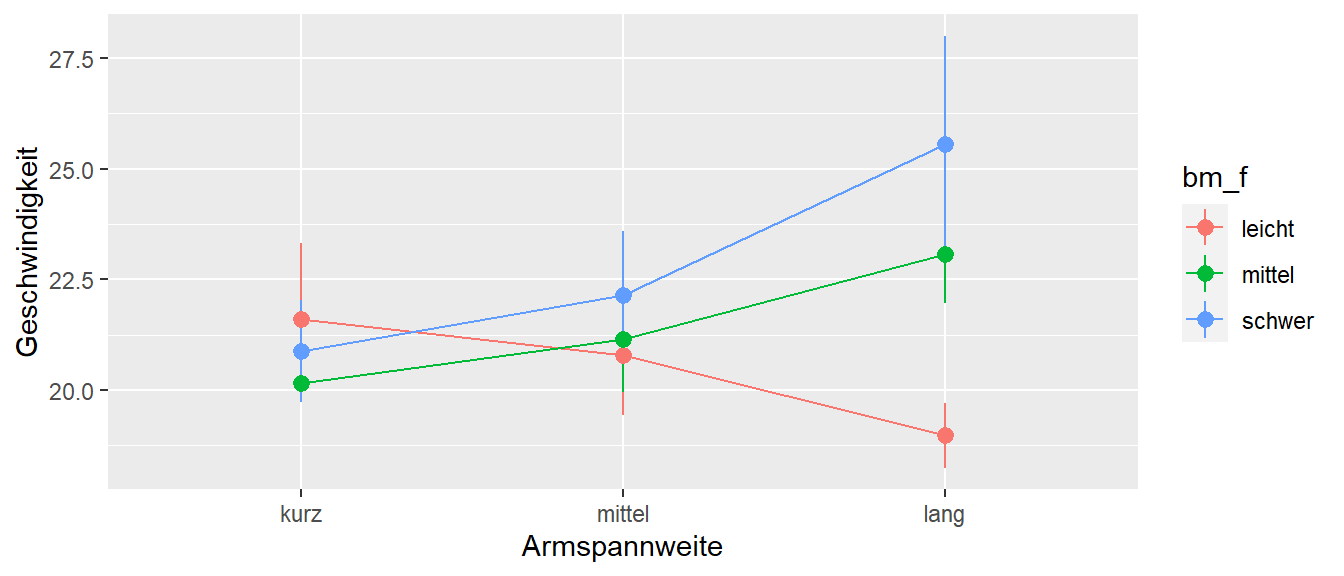
In dem Graphen zeigt sich ein interessantes Muster. Für mittel und schwere Handballer nimmt die Wurfgeschwindigkeit mit der Armspannweite zu. Dagegen ist der Trend gegensätzliche für leichte Handballer. D.h. der Einfluss der Armspannweite hängt davon ab wie schwer der Handballer ist. Der Einfluss ist in der anderen Richtung genauso, der Einfluss der Körpermasse hängt von der Armspannweite ab. Wenn sich die Effekte zweier Prädiktorvariablen gegenseitig beeinflussen, dann wird dies als Interaktionseffekts bezeichnet.
18.1.1 Kontinierlichen zu nominaler Variable in R
Um die Unterteilung einer kontinuierlichen Variablen in eine nominale Variable durchzuführen, kann in R die cut_number()-Funktion aus dem tidyverse verwendet werden. Die Parameter der Funktion sind die kontinuierliche Variable und die Anzahl der gewünschten Kategorien. Über den Parameter labels können die Bezeichnungen angepasst werden.
hb_quick <- handball |>
dplyr::mutate(
as_f = cut_number(arm_span_c, 3, labels=c('kurz','mittel','lang')),
bm_f = cut_number(body_mass_c, 3, labels=c('leicht','mittel','schwer'))
) cut_number() unterteilt den Wertebereich der Variablen so, dass die Anzahl der Datenpunkte pro Kategorie ungefähr gleich sind. Eine verwandte Funktion ist cut_interval() die die Kategoriengrenzen so bestimmt, dass die Intervall ungefähr gleich groß sind, unabhängig davon wie viele Datenpunkte in den jeweiligen Kategorien sind.
18.2 Interaktion zwischen zwei Effekten
Definition 18.1 (Interaktionseffekt) Wenn der Effekt einer unabhängigen Variable auf die abhängige Variable davon abhängt welche Ausprägung eine weitere unabhängige Variable hat, dann wird dies als ein Interaktionseffekt bezeichnet.
In Abgrenzung zu Interaktionseffekte werden die normalen Effekte als Haupteffekte bezeichnet.
Definition 18.2 (Haupteffekte ) Haupteffekte beschreiben den isolierten Einfluss einer unabhängigen Variable auf die abhängige Variable, unabhängig von anderen Variablen im Modell.
Im Rahmen eines linearen Modells, wird ein solcher Interaktionseffekt durch einen multiplikativen Term zwischen den beiden Variablen modelliert.
\[\begin{equation} Y_{i} = \beta_0 + \beta_1 \times \textrm{bodymass}_i + \beta_2 \times \textrm{armspan}_i + \beta_3 \times \textrm{bodymass}_i \times \textrm{armspan}_i + \epsilon_i \label{mlm-inter-model-ex} \end{equation}\]
In der Formel \(\eqref{mlm-inter-model-ex}\) ist neben den beiden Mdeollkoeffizienten \(\beta_1\) und \(\beta_2\) jetzt ein weitere Koeffizienten \(\beta_3\) der den Interaktionseffekt abbildet. Die \(X\)-Werte die diesem Modellkoeffizienten zugeordnet sind, berechnen sich aus Produkt aus den beiden beteiligten Prädiktorvariablen. In dem vorliegenden Handballbeispiel aus dem Produkt aus Armspannweite und Körpergewicht body_mass \(\times\) arm_span. Dies ist der Interaktionseffekt.
Warum die Multiplikation zwischen den Prädiktorvariablen sinnvoll ist, wird etwas später genauer betrachtet.
18.2.1 Interaktionseffekte in lm()
In R wird ein Interaktionseffekt in der Formel mittels eines : spezifiziert.
mod_3 <- lm(vel ~ body_mass_c + arm_span_c + body_mass_c:arm_span_c, handball) Um sich etwas Tipparbeit zu sparen, kann auch die Kurzform * benutzet werden. Hier multipliziert R die beiden beteiligten Variablen selbst aus.
mod_3 <- lm(vel ~ body_mass_c * arm_span_c, handball) D.h. die Funktion lm() multipliziert Terme der Form A*B in A + B + A:B aus.
Angewendet auf das Handballbeispiel folgt daraus die folgende Modellanpassung (siehe Tabelle 18.5)
| \(\hat{\beta}\) | \(s_e\) | t | p | |
|---|---|---|---|---|
| (Intercept) | 21.346 | 0.143 | 149.296 | <0.001 |
| body_mass_c | 0.119 | 0.015 | 8.133 | <0.001 |
| arm_span_c | 0.083 | 0.019 | 4.380 | <0.001 |
| body_mass_c:arm_span_c | 0.021 | 0.002 | 12.633 | <0.001 |
| \(\hat{\sigma}\) | 0.868 |
Bei Betrachtung der Residualvarianz \(\hat{\sigma}\) ist zu beobachten, dass sich der halbiert hat. D.h das Interaktionsmodell scheint deutlich präziser den Zusammenhang zwischen den Prädiktorvariablen und der abhängigen Variablen abbilden zu können, als dies bei dem rein additiven Modell der Fall war. Zusätzlich haben sich die Standardfehler der beiden Steigungskoeffizienten für die Haupteffekte deutlich verringert (vgl. Tabelle 18.3). Beide Koeffizienten sind nun statistisch signifikant geworden. Der neu dazugekommene Koeffizient für den Interaktionseffekt ist ebenfalls statistisch signifikant mit einem sehr kleinen Standardfehler. D.h die Hinzunahme des Interaktionseffekts hat in dem vorliegenden Beispiel dazu geführt, dass der Modellfit deutlich verbessert wurde. Im nächsten Schritt soll nun die Wirkung des Interaktionseffekt noch einmal deutlicher herausgearbeitet werden.
18.3 Koeffizienten im Interaktionsmodell verstehen
Im weiteren wird genauer betrachtet wie die Modellkoeffizienten und insbesondere der Interaktionseffekt \(\beta_3\) interpretiert werden kann. Dazu werden zunächst die Vorhersagen \(\hat{y}_i\) unter den beiden Modellen Modell 2, dem additiven Modell, und Modell 3, dem Interaktionsmodell, miteinander verglichen. Zur Erinnerung, beide Modell arbeiten mit zentrierten Prädiktorvariablen.
Um einen besseren Überblick über die Vorhersagen zu bekommen, ist es hilfreich die Daten zu vereinfachen indem nur drei verschiedene Werte für die Armspannweite \(as = \{-10,0,10\}\) cm. D.h. einen hypothetischen Handballer mit der Durchschnittsspannweite, sowie jeweils einen mit \(10\) cm kürzerer bzw. \(10\) cm längerer Spannweite. Der gleiche Ansatz wird auf für die Körpermasse gewählt, indem hier ebenfalls drei verschiedenen Körpermassen \(bm = \{-2,0,2\}\) Kg verwendet werden. D.h. eine Person mit durchschnittlicher Körpermasse und jeweils eine Person mit \(-2\) und \(2\) Kg leichter bzw. schwerer. Dies führt zu der folgenden Kombination von Prädiktorvariablen (siehe Tabelle 18.6).
| Armspannweite | Körpermasse |
|---|---|
| -10 | -2 |
| 0 | -2 |
| 10 | -2 |
| -10 | 0 |
| 0 | 0 |
| 10 | 0 |
| -10 | 2 |
| 0 | 2 |
| 10 | 2 |
Für diese Daten wird nun die vorhergesagten Wert \(\hat{y}_i\) unter beiden Modellen berechnet und graphisch dargestellt (siehe Abbildung 18.4). Diese Art der Darstellung des Zusammenhangs zwischen einer Prädiktorvariable und der abhängigen Variable während weitere Prädiktorvariablen konstant gehalten werden, wird als einfache Steigungen bezeichnet.
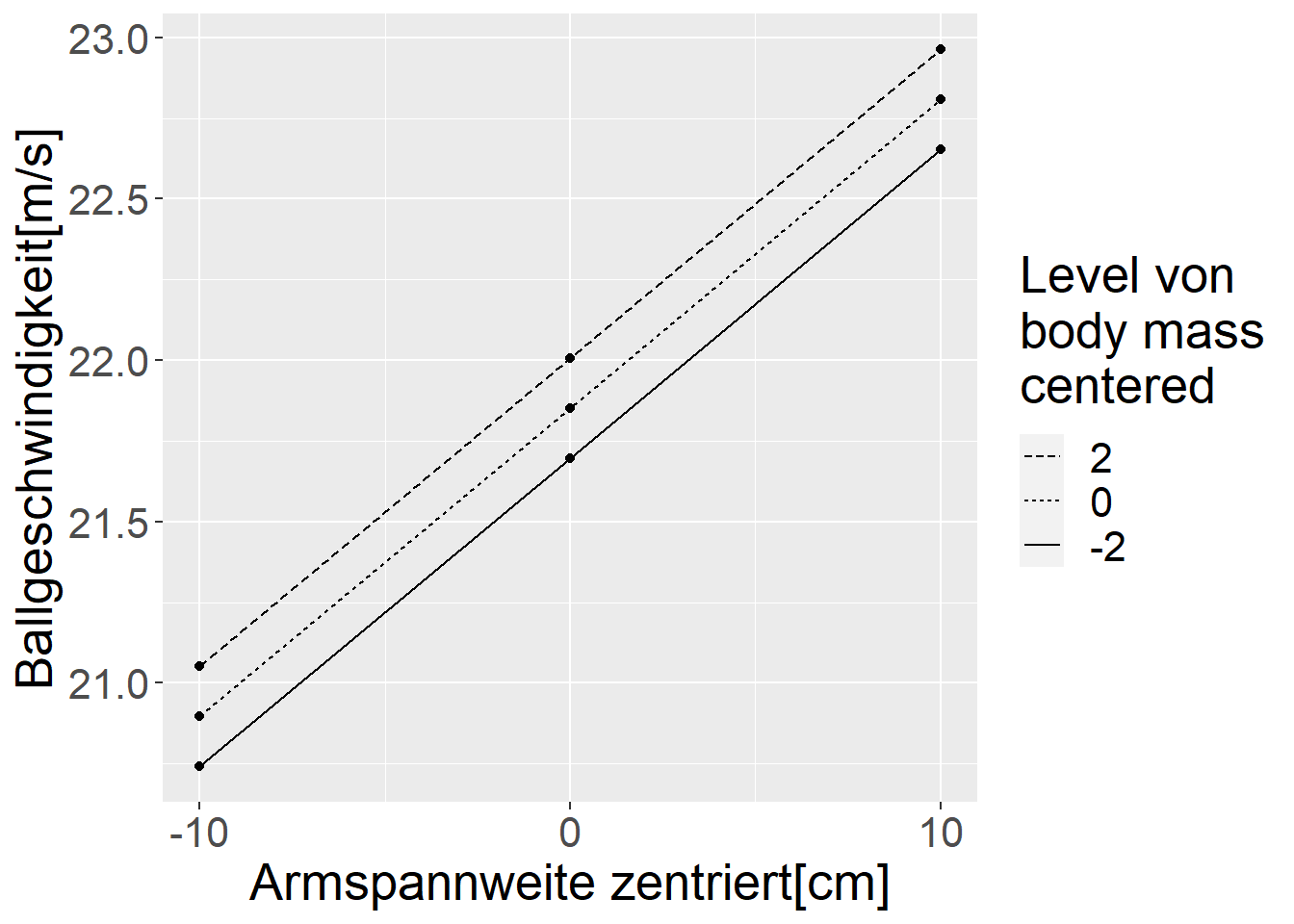
In Abbildung 18.4 (a) ist zu sehen, dass die vorhergesagten Werte \(\hat{y}_i\) für verschiedene Körpermassen jeweils nur parallel gegeneinander verschoben sind. Da die Unterschiede zwischen den Körpermassen sich um jeweils \(2\) Kg unterscheiden, sind für einen gegebenen Wert der Armspannweite die Abstände zwischen den Linien konstant um den Faktor \(\beta_{\text{body mass}} \times 2\). D.h. egal welchen Wert die Armspannweite einnimmt, der Zusammenhang der Körpermasse mit der Wurfgeschwindigkeit bleibt gleich.
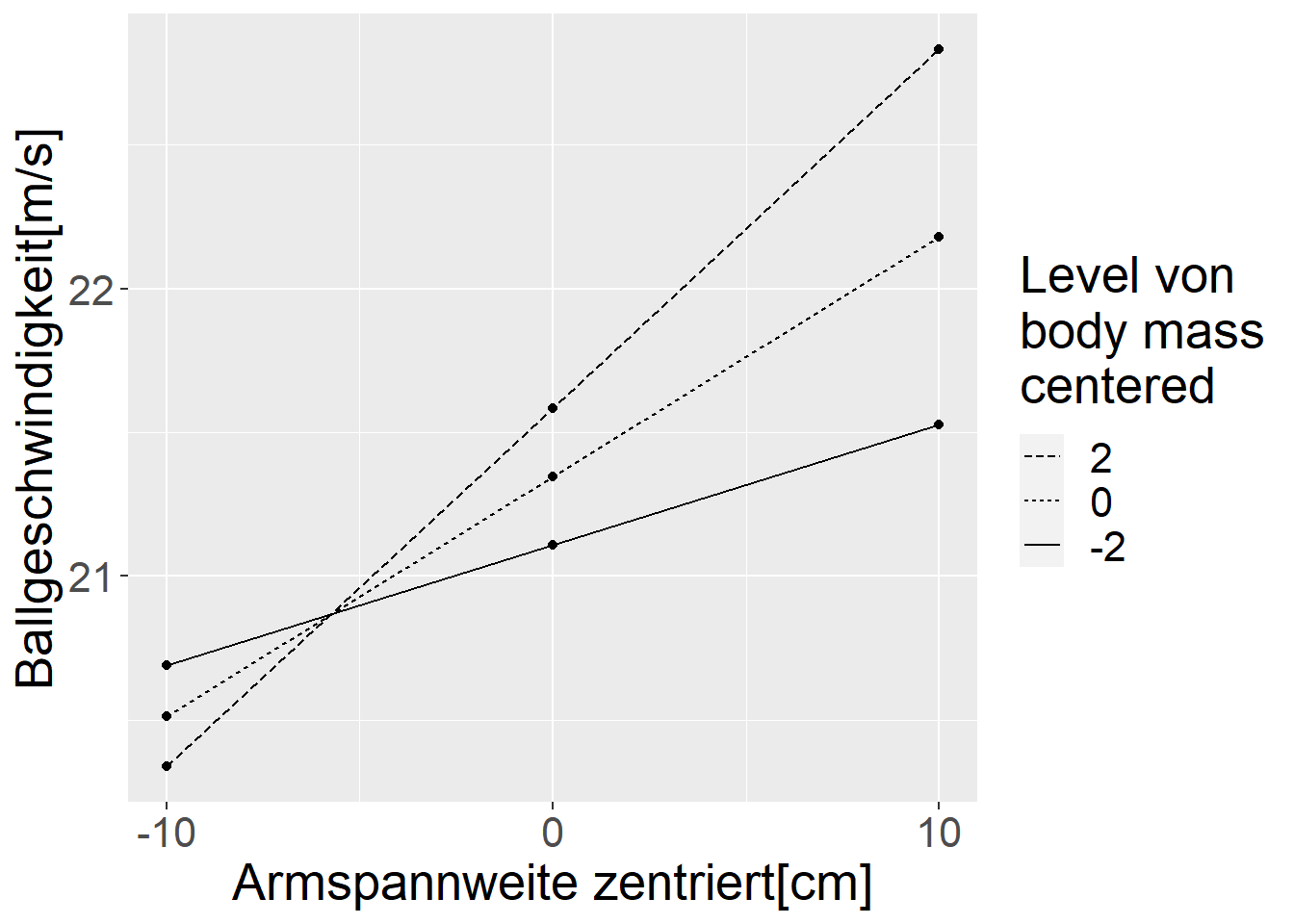
Unter Modell 3 fallen die einfachen Steigung dagegen vollkommen anders aus (siehe Abbildung 18.4 (b)). Hier kann beobachtet werden, dass die Unterschiede zwischen den verschiedenen Armspannweiten davon abhängen wie schwer ein Handballer ist. Während bei kleinen Armspannweiten die Unterschiede eher gering ausfallen, werden die Unterschiede zwischen den drei gewählten Gewichtskategorien umso größer je größer die Armspannweite wird. Es handelt sich eben um einen Interaktionseffekt. Es ist weiter sehen, dass bei einer Armspannweite von \(-5\) cm es sogar zum schneiden der einfachen Steigungen kommt. In diesem Fall führt dies dazu, dass sich die Anordnung der Wurfgeschwindigkeiten in Abhängigkeit von der Körpermasse umkehrt. Während bei Armspannweite von \(-10\)cm eine leichtere Person die höchste Wurfgeschwindigkeit produziert, ist dies bei einer Armspannweite von \(+10\)cm ein schwerere Person (in diesem Vergleich immer in Bezug auf die gewählten Wertebereiche).
Generell ist ein Interaktionseffekt dabei immer symmetrisch und hängt nicht davon ab, welche Variable als \(X\)-Variable in dem Graphen verwendet wird. Wenn die Änderung der einen Variable \(A\) davon abhängt welchen Wert die andere Variable \(B\) hat, dann gilt dies auch anderes herum für die Veränderung von Variable \(B\) in Abhängigkeit vom Wert der Variablen \(A\). Um diese Symmetrie zu verdeutlichen sind in Abbildung 18.5 beide Möglichkeiten der Darstellung der einfachen Effekte nebeneinander dargestellt.
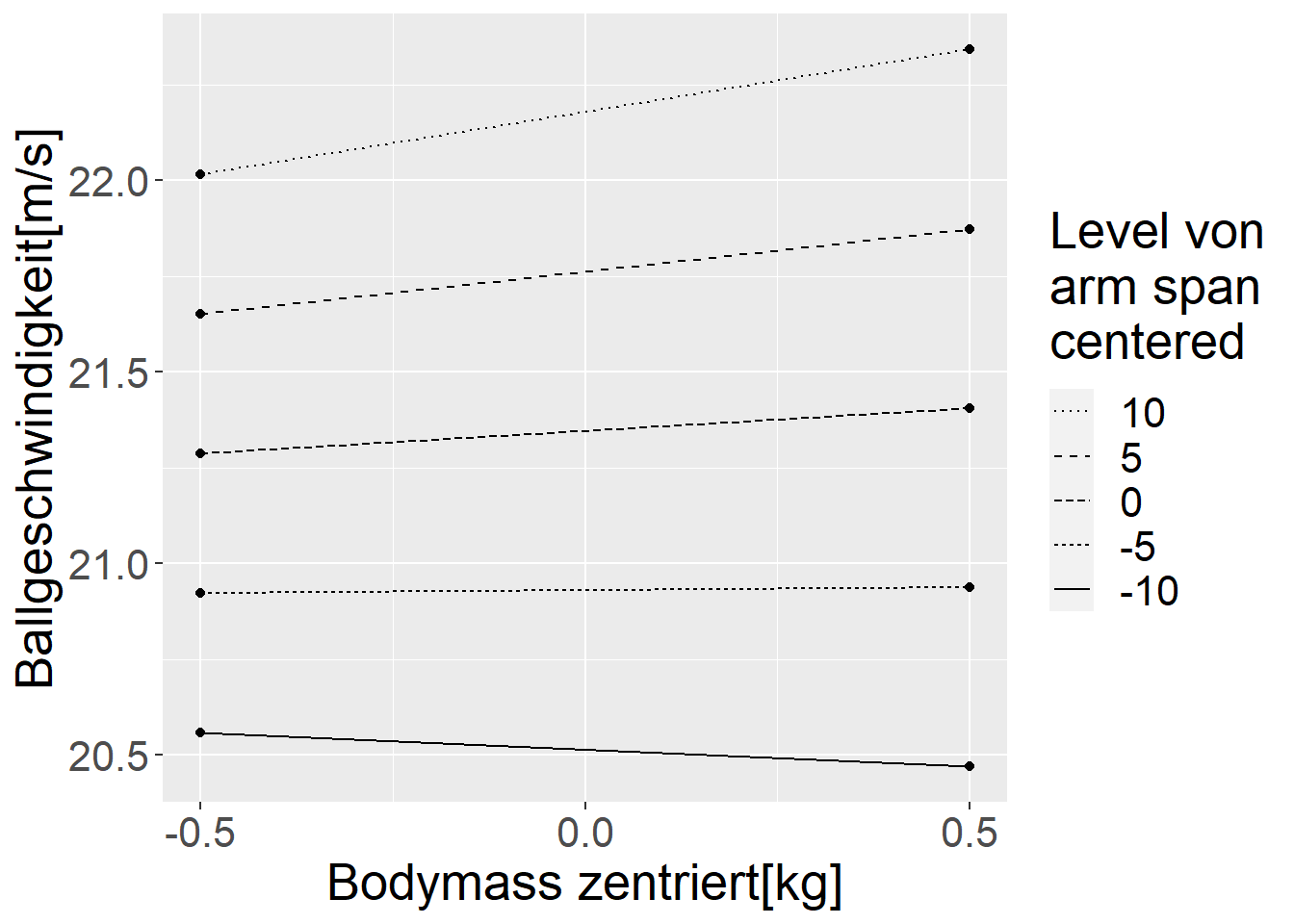
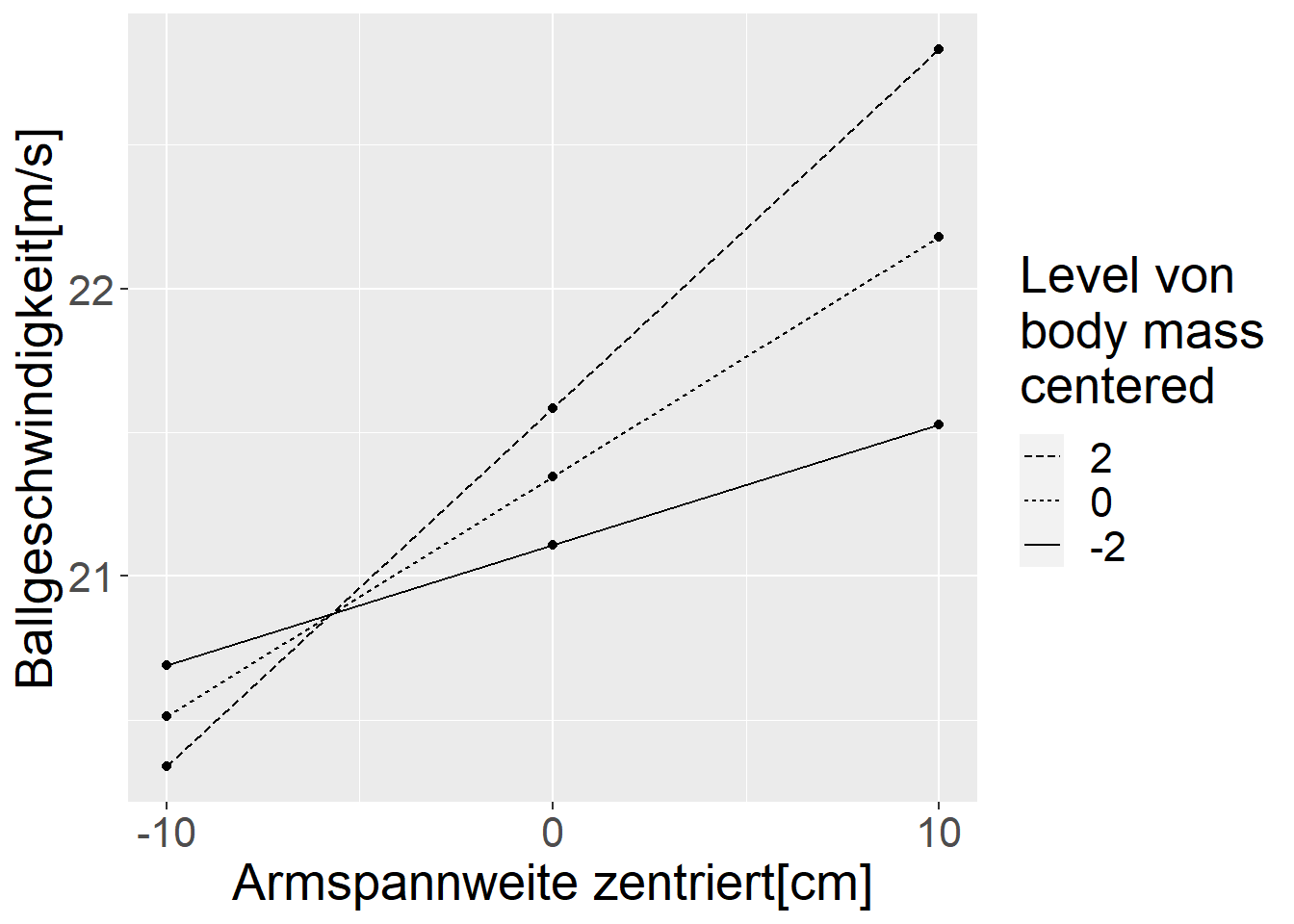
In beiden Fällen ist ein Interaktionseffekt zu beobachten. Die genau Ausprägung der einfachen Steigungen ist dabei abhängig von Varianzen der Prädiktorvariablen, d.h. wie stark die Werte streuen, bzw. von de gewählten Einheiten.
18.3.1 Interaktionseffekte deep-dive
Als nächstes Versuchen soll untersucht werden, warum die Multiplikation der an der Interaktion beteiligten Prädiktorvariablen sinnvoll ist um die Interpretation der Koeffizienten in Tabelle 18.5 numerisch besser bedeuten zu können. In Abbildung 18.6 sind noch einmal die einfachen Steigungen für die Körpermasse in Abhängigkeit von der Armspannweite dargestellt.
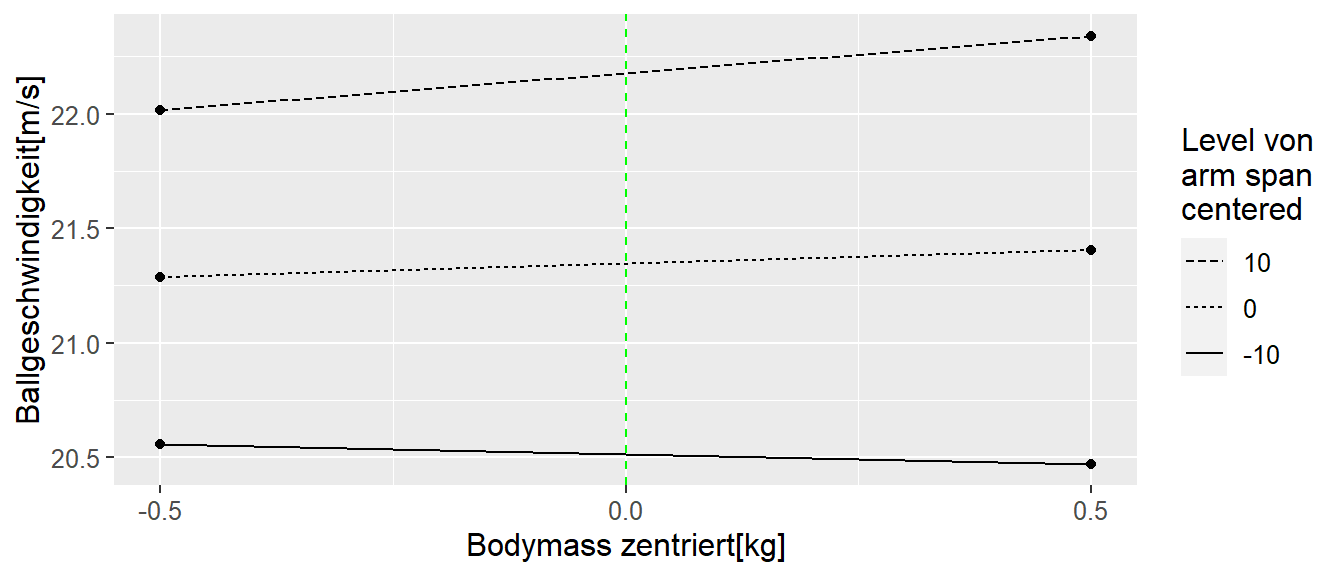
Wie bereits beschrieben, es ist zu beobachten, dass der Zusammenhang zwischen der Wurfgeschwindigkeit und der Körpermasse von der gewählten Armspannweite abhängt. Um die Bedeutung der Koeffizienten in einen Interaktionsmodell besser zu verstehen, werden nun die einfachen Steiungen für die drei abgebildeten Graphen berechnet. D.h. es wird dreimal eine einfache lineare Regression berechnet. In Tabelle 18.7 sind die dazugehörenden Steigungskoeffizienten für die einfachen Steigungen abgebildet. \(\beta_0\) ist der \(y\)-Achsenabschnitt für die jeweiligen Armspannweiten und \(\beta_1\) die jeweiligen Steigungen.
| Armspannweite (zentriert) | \(\beta_0\) | \(\beta_1\) |
|---|---|---|
| 10 | 22.178 | 0.326 |
| 0 | 21.346 | 0.119 |
| -10 | 20.514 | -0.088 |
| \(\beta\) | |
|---|---|
(Intercept) |
21.346 |
bm_c |
0.119 |
as_c |
0.083 |
bm_c:as_c |
0.021 |
Entsprechend den Graphen in Abbildung 18.6 ist der Steigungskoeffizient für \(\beta_1\) für die Armspannweiten \(0\) und \(10\) positive, während er bei der Armspannweite \(-10\) negativ ist. Ein Vergleich dieser Wert mit denjenigen aus dem Interaktionsmodell in Tabelle 18.7 (b) zeigt, dass die Werte unterschiedlich sind. Um nun nachzuvollziehen, dass die Werte in Tabelle 18.7 (a) aus denjenigen in Tabelle 18.7 (b) resultieren sind ein paar Vereinfachungen notwendig.
Sei zunächst einmal die zentrierte Körpermasse auf \(\text{bodymass} = 0\). D.h. in Abbildung 18.6 bewegen wir uns entlang der eingezeichneten, grünen Linie. Wenn ein Handballer nun ebenfalls eine durchschnittliche Armspannweite hat, also \(\text{armspan} = 0\) dann wird eine Wurfgeschwindigkeit von \(v = 21.346\) vorhergesagt. D.h. \(\text{bodymass} = 0\) und \(\text{armspan} = 0\) also genau der \(Y\)-Achsenabschnitt in Modell 3. Sei nun ein Handballer mit durschnittlicher Körpermasse aber einer Armspannweite von \(+10\) cm also \(cm = 10\) gegeben. In Abbildung 18.6 würde das einer vertikalen Beweung entlang der grünen Linie nach oben entsprechen. In Modellkoeffizienten gesprochen bedeutet dies:
\[\begin{align*} \hat{y} &= 21.346 + 0.119 \cdot 0 + 0.083 \cdot 10 + 0.021 \cdot 0 \cdot 10 \\ &= 21.346 + 0.83 = 22.175 \end{align*}\]
Der Wert ist, bis auf ein paar Rundungsfehler, dem \(Y\)-Achsenabschnitt \(\beta_0\) in Tabelle 18.7 (a) unter Armspannweite \(=10\) gleich, \(22.175 \approx 22.178\). Das gleiche Prinzip kann ebenfalls angewendet werden, wenn die Armspannweite um \(10\)cm verkürzt wird. D.h. in Abbildung 18.6 entlang der grünen Linie nach unten. In Modellkoeffizienten resultiert dies in:
\[\begin{align*} \hat{y} &= 21.346 + 0.119 \cdot 0 + 0.083 \cdot -10 + 0.021 \cdot 0 \cdot 10 \\ &= 21.346 - 0.83 = 20.516 \end{align*}\]
Dies entspricht wieder, bis auf Rundungsfehler, dem \(Y\)-Achsenabschnitt in Tabelle 18.7 (a) unter dem Eintrag für Armspannweite \(-10\) (\(20.516 \approx 20.514\)).
Sei nun ein Handballer mit einer Armspannweite von \(as = 0\) gegeben. Dann können die Koeffizienten in Tabelle 18.7 (b) direkt abgelesen werden. Die Wurfgeschwindigkeit verändert sich somit mit der Körpermasse über den Koeffizienten \(\beta_{bm_c} = 0.119\). Eingesetzt in die Modellgleichung führt dies zu:
\[\begin{align*} \hat{y} &= 21.346 + 0.119 \cdot bm_c + 0.083 \cdot 0 + 0.021 \cdot bm_c \cdot 0 \\ &= 21.346 + 0.119 \cdot bm_c \end{align*}\]
Als nächstes wird der Fall betrachtet, wenn beide Prädiktorvariablen \(as\neq 0\) und \(bm\neq 0\) sind. Sei zum Beispiel \(as = 10\). Wie verändert sich der vorhergesagte Wert \(\hat{y}_i\) mit der Körpermasse \(bm_c\). \(bm_c\) bleibt offen um die Steigungsgleichung zu bestimmen. Wieder eingesetzt in das Modell ergibt dies:
\[\begin{align*} \hat{y} &= 21.346 + 0.119 \cdot bm_c + 0.083 \cdot 10 + 0.021 \cdot bm_c \cdot 10 \\ &= 21.346 + 0.83 + 0.119 \cdot bm_c + 0.21 \cdot bm_c \\ &= 22.175 + (0.119 + 0.21) \cdot bm_c \\ &= 22.175 + 0.329 \cdot bm_c \end{align*}\]
Bis auf ein paar Rundungsfehler, werden die Steigungskoeffizienten der Geradengleichung in Tabelle 18.7 (a) für den Eintrag as = 10 erhalten.
In Bezug auf die Interpretation der Modellkoeffizienten ergibt sich somit das folgende Bild. Der Modellkoeffizient \(\beta_0\) beschreibt den \(y\)-Achsenabschnitt wenn alle Prädiktorvariablen den Wert \(0\) annehmen. Wenn einer der beiden Prädiktorvariablen \(0\) ist, dann beschreibt der andere Modellkoeffizient die Verschiebung des \(Y\)-Achsenabschnitts der einfachen Gerade deren Steigung durch den Modellkoeffizienten beschrieben wird. Wenn beide Prädiktorvariablen \(neq 0\) sind, dann kommt erst der Interaktionskoeffizient ins Spiel und führt zu einer Veränderung der einfachen Steigung in Abhängigkeit von der Kombination der Prädiktorvariablen.
Übungsaufgabe 18.1 Versuche anhand der Koeffizienten in Tabelle 18.7 (b) die einfache Steigungsgleichung für \(as_c = -10\) zu erhalten.
Zusammenfassend lässt sich die folgende Interpretation der Koeffizienten in einem Interaktionsmodell mit zwei Prädiktorvariablen formulieren.
\[\begin{equation*} Y = b_0 + b_1 \cdot x_1 + b_2 \cdot x_2 + b_3 \cdot x_1 \cdot x_2 + \epsilon_i \end{equation*}\]
- \(b_0\): (y-Achsenabschnitt) der Wert von \(\hat{Y}\) wenn \(x_1 = 0\) und \(x_2 = 0\) gilt.
- \(b_1\): Der Unterschied in \(\hat{Y}\) wenn zwei Objekte sich in \(x_1\) um eine Einheit unterscheiden und \(x_2 = 0\) ist (Haupteffekt).
- \(b_2\): Der Unterschied in \(\hat{Y}\) wenn zwei Objekte sich in \(x_2\) um eine Einheit unterscheiden und \(x_1 = 0\) ist (Haupteffekt).
- \(b_3\): (Interaktionskoeffizient) Die Veränderung des Effekts von \(x_1\) auf \(\hat{Y}\) wenn \(x_2\) um eine Einheit größer wird bzw. genau andersherum für \(x_2\).
18.4 Die Form der Modellfläche unter dem additiven und der Interaktionsmodell
Abschließend nun eine Betrachtung der resultierenden Flächen unter additiven und dem Interaktionsmodell. In Abbildung 18.7 sind die gefitteten Flächen und die Residuen unter den beiden Modellen abgebildet.
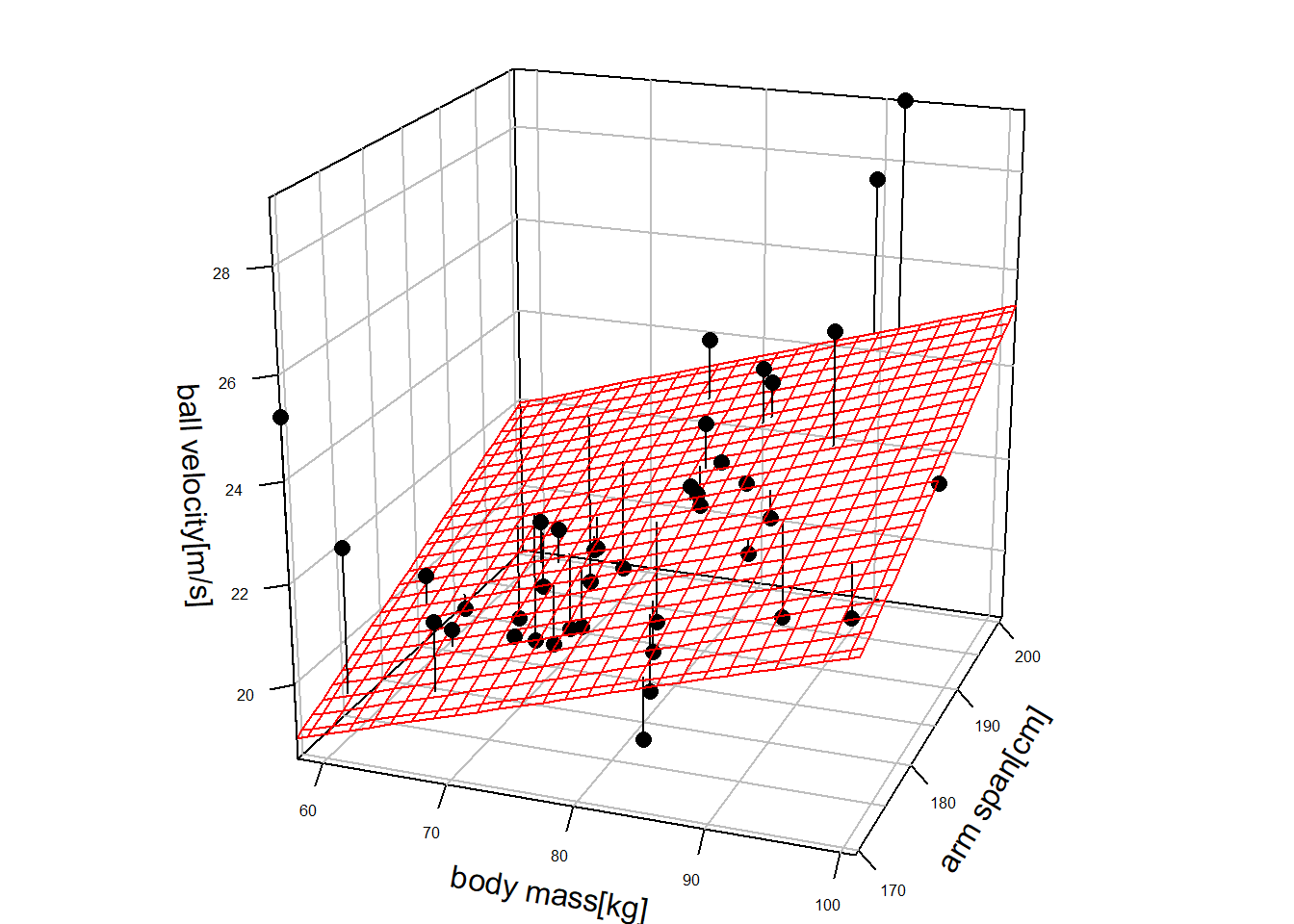
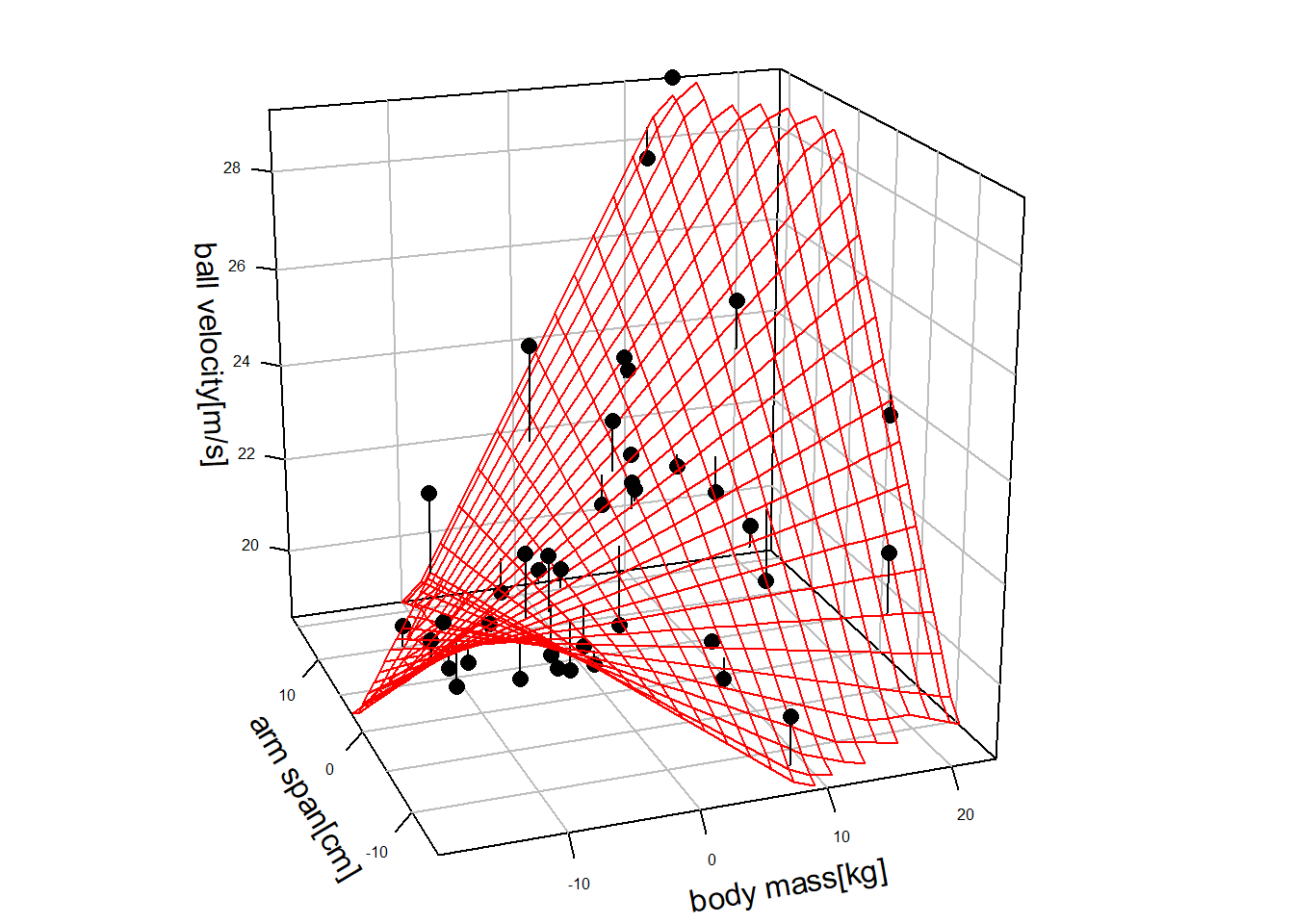
Unter dem Interaktionsmodell ist die gefittete Fläche keine einfache Ebene mehr, sondern durch die Hinzunahme des Interaktionseffekts ähnelt die Fläche nun eher einem Sattel. D.h. durch die Integration von Interaktionseffekte zwischen den Prädiktorvariablen können deutlich komplizierte Zusammenhänge zwischen den Prädiktorvariablen und der abhängigen Variable modellieren werden. Die Komplexität erhöht sich entsprechend mit der Zahl der Prädiktorvariablen und den möglichen Interaktion zwischen diesen.
Zurückkommend auf unser Ausgangsbeispiel mit den Handballdaten, kann entsprechend die Auswirkung auf den die Modellanpassung analysiert werden. Dazu ein Vergleich der beiden Residuenplots (siehe Abbildung 18.8).
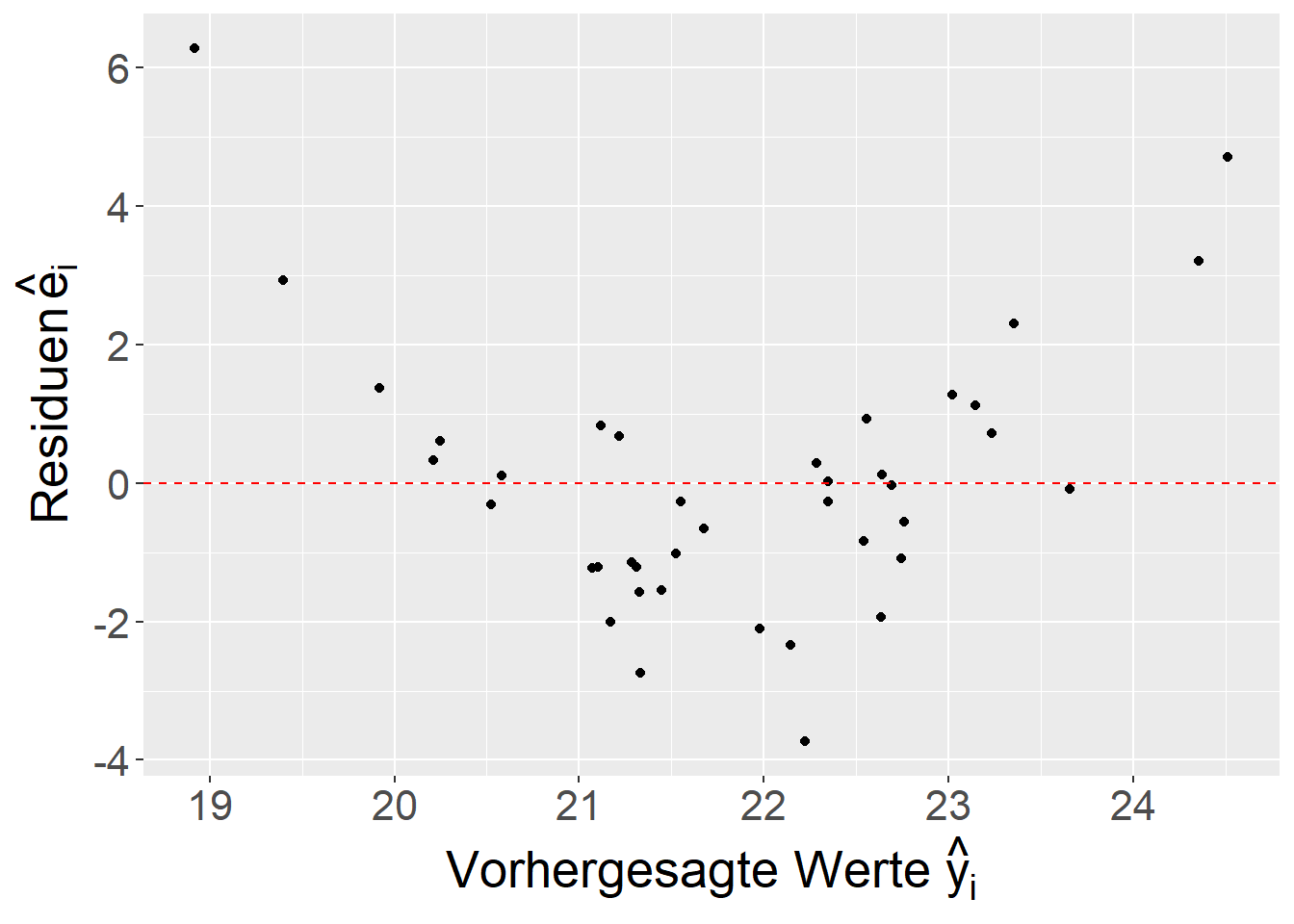
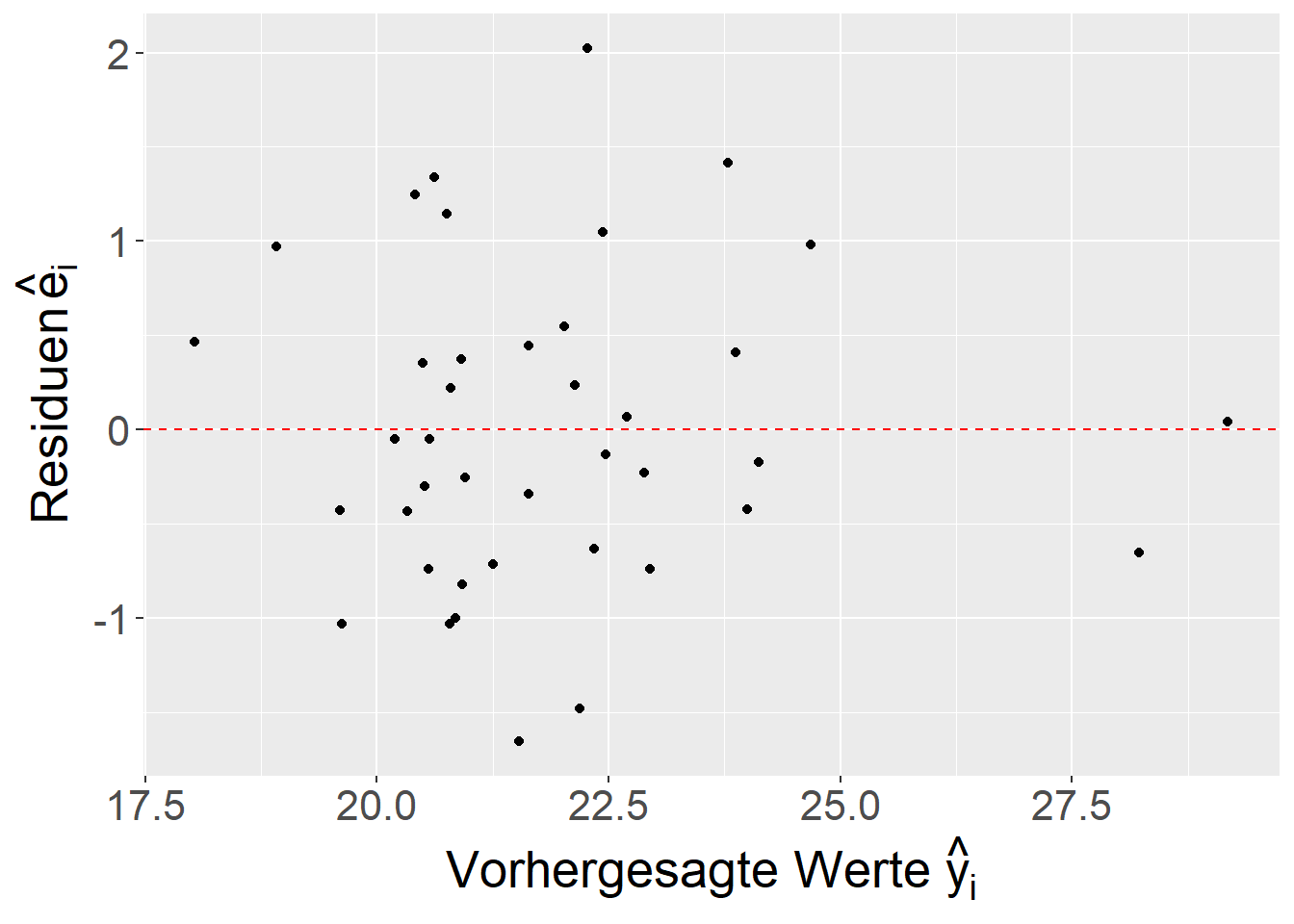
Es ist zu beobachten, dass in Abbildung 18.8 (b) die Struktur, die im additiven Modell in Abbildung 18.8 (a) für die Residuen , nun nicht mehr vorhanden ist. Ähnlich verhält sich auch der Vergleich für die die qq-Plots der Residuen (siehe Abbildung 18.9).
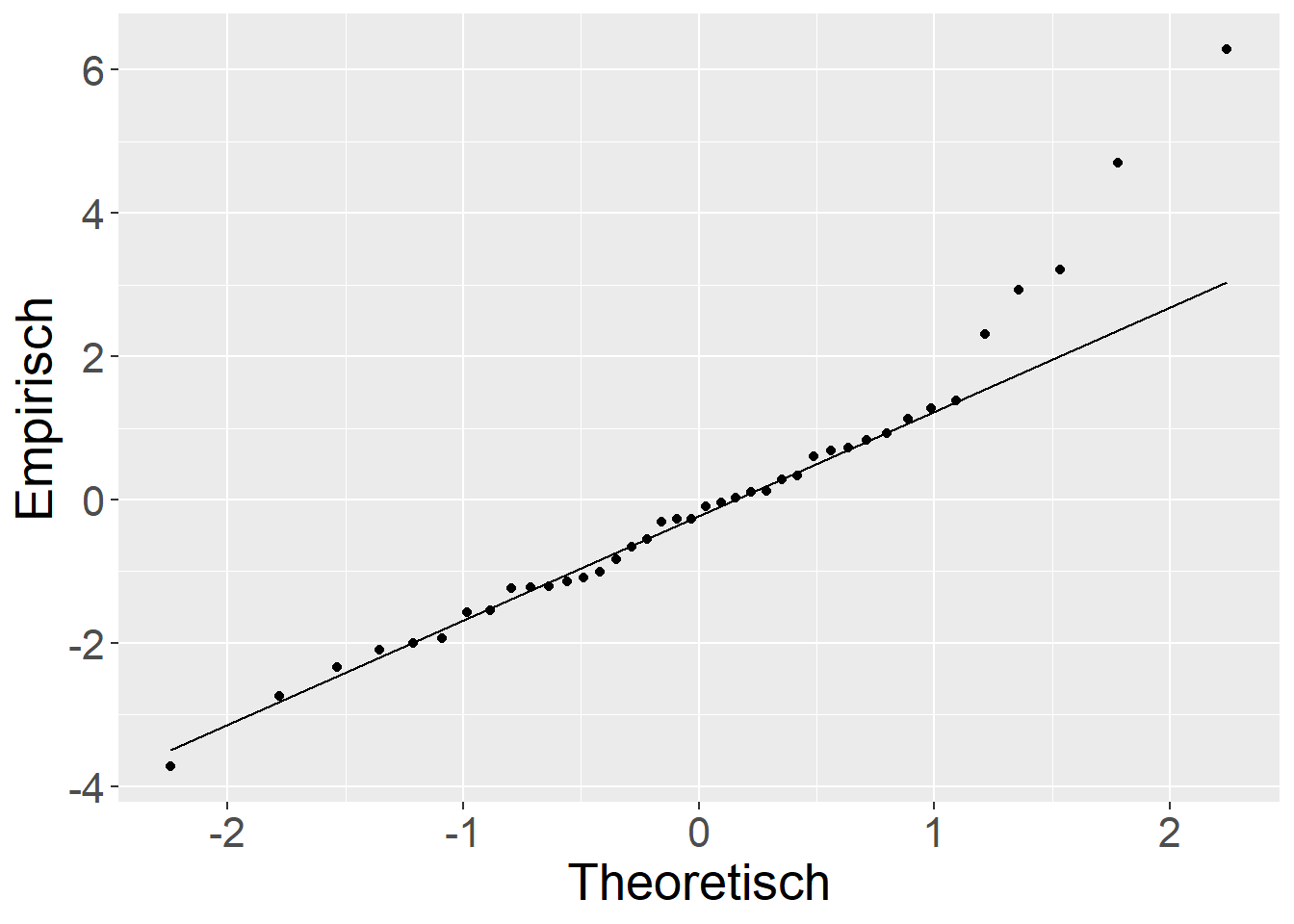
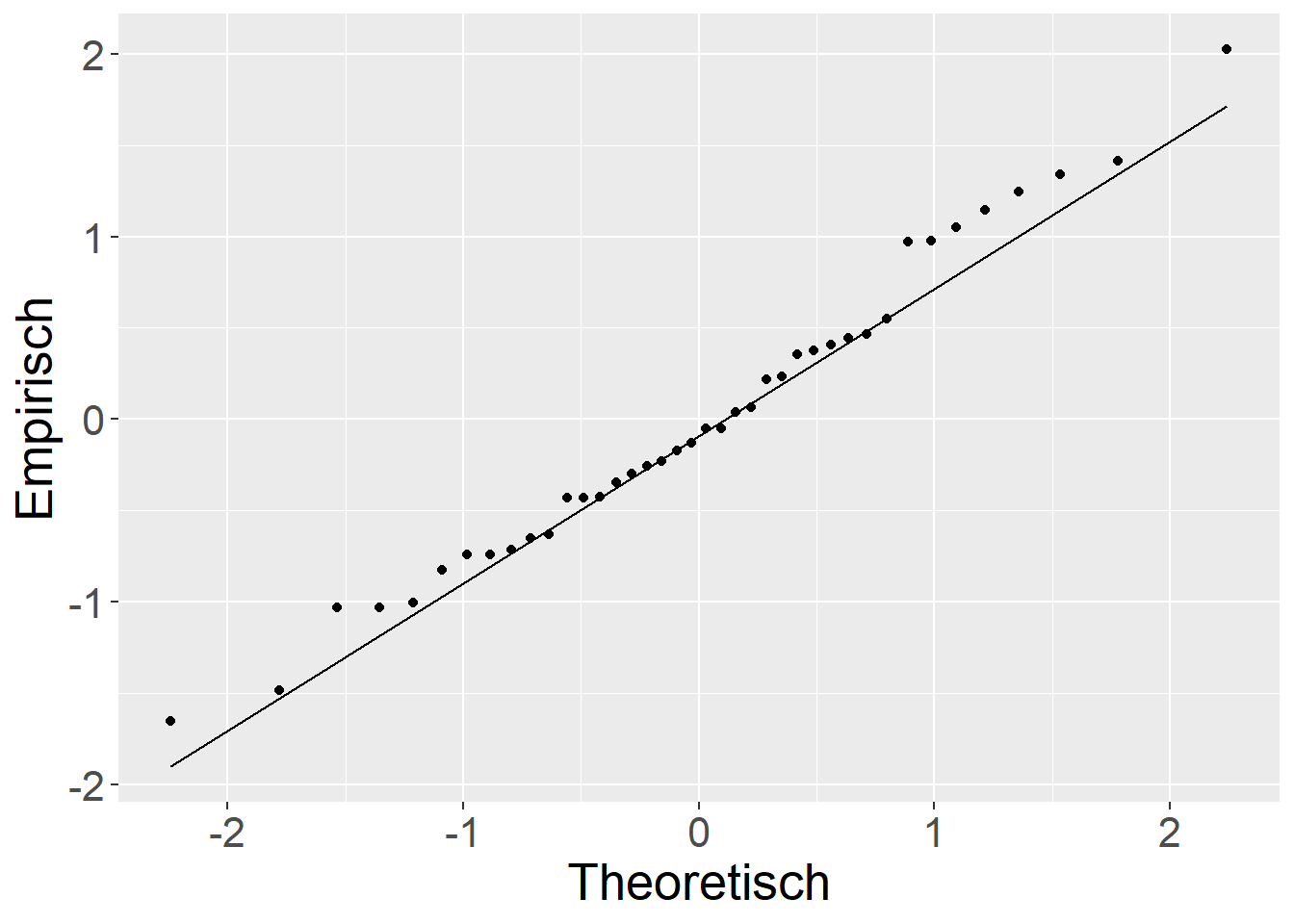
Dazu nun ein Vergleich der weiteren Performanceparameter.
| Name | Model | R2 | R2_adjusted | RMSE | Sigma |
|---|---|---|---|---|---|
| mod_2 | lm | 0.291 | 0.252 | 1.919 | 1.996 |
| mod_3 | lm | 0.869 | 0.859 | 0.824 | 0.868 |
Insgesamt sind durch die Hinzunahme des Interaktionseffekt nicht nur die Standardfehler und der Residualfehler verringert worden, sondern das Modell fittet die Daten auch deutlich besser als das additive Modell. Dies ist natürlich nicht immer der Fall, sondern hängt eng mit den jeweiligen Daten zusammen.
18.5 Modelmatrix in R unter dem Interaktionsmodell
Um die Modellmatrix bei Interaktionsmodell sei wieder der einfache Datensatz aus dem letzten Kapitel genommen.
df <- tibble(
y = c(1,3,2.5,7),
x_1 = 1:4,
x_2= c(11,11,14,13)
)Die Anwendung der Funktion model.matrix() mit einem Interaktionsterm zwischen x_1 und x_2 führt zu folgender Darstellung.
model.matrix(~x_1 + x_2 + x_1:x_2, df) (Intercept) x_1 x_2 x_1:x_2
1 1 1 11 11
2 1 2 11 22
3 1 3 14 42
4 1 4 13 52
attr(,"assign")
[1] 0 1 2 3Es ist zu beobachten, dass eine weitere Spalte für den Interaktionsterm zur Modellmatrize hinzugefügt wurde. Die Werte sind dabei genau das Ergebnis der Multiplikation zwischen den Werten von x_1 und x_2.
Wie oben schon erwähnt führt ~x_1 * x_2 zum gleichem Ergebnis.
model.matrix(~x_1 * x_2, df) (Intercept) x_1 x_2 x_1:x_2
1 1 1 11 11
2 1 2 11 22
3 1 3 14 42
4 1 4 13 52
attr(,"assign")
[1] 0 1 2 318.6 Take-away
Das Interaktionsmodell:
- Erhöht die Flexibilität des linearen Modells.
- Bei Interaktionen hängt der Einfluss der einzelnen Variablen immer von den Werten der anderen Variablen ab.
- Achtung: Interpretation der einfachen Haupteffekte oft nicht mehr möglich bzw. sinnvoll!
18.7 Einfluss der Zentrierung auf die Koeffizienten im Interaktionsmodell (advanced)
Schauen wir uns noch zum Abschluss noch an, was algebraisch mit dem Koeffizienten im Interaktionsmodell passiert wenn die Prädiktorvariablen \(x_{ki}\)s zentriert werden.
\[\begin{align*} y_i &= \beta_0 + \beta_1 (x_{1i} - \bar{x}_1) + \beta_2 (x_{2i} - \bar{x}_2) + \beta_3 (x_{1i}-\bar{x}_1)(x_{2i}-\bar{x}_2) \\ &= \beta_0 + \beta_1 x_{1i} - \beta_1 \bar{x}_1 + \beta_2 x_{2i} - \beta_2 \bar{x}_2 + \beta_3 x_{1i} x_{2i} - \beta_3 x_{1i} \bar{x}_2 - \beta_3 \bar{x}_1 x_{2i} + \beta_3 \bar{x}_1 \bar{x}_2 \\ &= \beta_0 - \beta_1 \bar{x}_1 - \beta_2 \bar{x}_2 + \beta_3 \bar{x}_1 \bar{x}_2 + \beta_1 x_{1i}- \beta_3 \bar{x}_2 x_{1i} + \beta_2 x_{2i} - \beta_3 \bar{x}_1 x_{2i} + \beta_3 x_{1i} x_{2i} \\ &= \underbrace{\beta_0 - \beta_1 \bar{x}_1 - \beta_2 \bar{x}_2 + \beta_3 \bar{x}_1 \bar{x}_2}_{\beta_0} + \underbrace{(\beta_1 - \beta_3 \bar{x}_2) x_{1i}}_{\beta_1 x_{1i}} + \underbrace{(\beta_2 - \beta_3 \bar{x}_1) x_{2i}}_{\beta_2 x_{2i}} + \beta_3 x_{1i} x_{2i} \end{align*}\]
Wir sehen, dass der Interaktionsterm tatsächlich gleich ist unter beiden Modellen. Dagegen unterscheiden sich die Koeffizienten der Haupteffekte deutlich voneinander. Der Übergang vom zentrierten zum unzentrierten Modell ist dabei nicht immer gleich, sondern hängt von den jeweiligen Werten dern Daten ab.
18.8 Zum Nacharbeiten
Kutner u. a. (2005, p.306–313)