27 Completely Randomized Factorial Design
Nachdem wir uns im vorhergehenden Abschnitt mit dem Completely Randomized Design Untersuchungsdesigns angeschaut haben, bei dem nur eine unabhängige nominale Variable variiert wurde, schauen wir uns jetzt den Fall an, wenn wir den Einfluss zweier nominale unabhängige Variablen auf eine abhängige Variable untersuchen wollen. Wie wir sehen werden führt dies zu einem zusätzlichen Effekt dem Interaktionseffekt. Inhaltlich bedeutet dies nicht allerdings erst mal gar nichts Neues, da wir Interaktionseffekt schon im Zusammenhang mit der multiplen Regression kennengelernt haben und die Interpretation daher auch nichts neues bedeutet. Daher wir ein Hauptaugenmerk in diesem Kapitel darin liegen, wir wir Interaktionseffekte interpretieren können bzw. welchen Einfluss diese auf die Interpretation von Haupteffekten bedeutet und welchen Einfluss Interaktionseffekte auf die Anzahl der notwendigen Replikationen haben um eine gewünschte Power zu gewährleisten. Generell wenn mehr als ein nominaler Faktor an dem Untersuchungsdesign beteiligt ist, dann wir von einem Completely Randomized Factorial Design (CRFD) gesprochen.
Die Annahmen beim CRDF sind die gleichen wie auch beim CRD. Seien ein CRFD mit zwei Faktoren \(A\) und \(B\) gegeben die jeweils \(p\) bzw. \(q\) Faktorstufen haben. Dann gelten die folgenden Annahmen.
- Unabhängige EUs
- Die EUs sind in die \(p\times q\) Gruppen eingeteilt worden
- Die Werte in jeder Gruppe sind Normalverteilt \(Y_{ijk} \sim \mathcal{N}(\mu_{ij}, \sigma^2)\) mit der gleichen Varianz \(\sigma^2\)
In der Literatur im Zusammenhang mit einem CRFD oft der Term Zellen verwendet. Dieser bezeichnet die jeweiligen Kombinationen der Faktorstufen. Sei zum Beispiel \(p = 3\) und \(q = 2\) dann erhalten wir die folgende Anordnung von Zellen (siehe Tabelle 27.1)
| \(A_1\) | \(A_2\) | \(A_3\) | |
| \(B_1\) | \(A_1B_1\) | \(A_2B_1\) | \(A_3B_1\) |
| \(B_2\) | \(A_1B_2\) | \(A_2B_2\) | \(A_3B_2\) |
Faktoren werden als gekreuzt bezeichnet, wenn alle Kombinationen der Faktoren beobachtet wurden.
27.1 Das statistische Modell im CRFD
Das statistische Modell im CRFD besteht in einer natürlichen Erweiterung des Modells für ein CRD. Die Modellstruktur ist die folgende:
\[\begin{equation} Y_{ijk} = \mu + \alpha_i + \beta_j + (\alpha\beta)_{ij} + \epsilon_{ijk}, \qquad \epsilon_{ijk}\sim \mathcal{N}(0,\sigma^2) \label{eq-ed-crfd-model} \end{equation}\]
\(i\) und \(j\) sind die Indikatoren der jeweiligen Fakorstufen für die Faktoren \(A\) und \(B\), während \(k\) der Indikator der jeweiligen EUs (Replikation) ist. \(\mu\) bezeichnet den Gesamtmittelwert und \(\alpha_i\) ist der Einfluss der \(i\)-ten Stufe von Faktor \(A\), \(\beta_j\) ist der Einfluss der \(j\)-ten Stufe von Faktor \(B\), und \((\alpha\beta)_{ij}\) bezeichent den Einfluss der Kombination der Faktoren \(A\) und \(B\) also den Interaktionsfaktor. Wenn wir das Modell im Sinne der vorher eingeführten Herleitung aus der multiplen Regression betrachten, dann werden die Effekte im Modell über Indikatorvariablen abgebildet.
Die folgenden Herleitung sind für ein balanciertes Modell, bei dem die Zellbesetzungen alle gleich sind, z.B. \(r\). In diesem Fall gilt für den Indikator \(k, k = 1, \ldots, r\) oder anders ausgedrückt, \(r_{ij} = r\) für alle \(i,j\).
Um wieder den uns bekannten Ansatz von Modellvergleichen durchzuführen, stellen wir wiederum eine Modellhierarchie auf. Das full model ist das eben beschriebene Modell (siehe Formel \(\eqref{eq-ed-crfd-model}\) während die reduzierten Modelle die folgende Reihenfolge ermöglichen:
\[\begin{align} Y_{ijk} &= \mu + \alpha_i + \beta_j + \epsilon_{ijk} \label{eq-ed-crfd-additiv} \\ Y_{ijk} &= \mu + \alpha_i + \epsilon_{ijk} \qquad (\textrm{alternativ}: Y_{ijk} = \mu + \beta_j + \epsilon_{ijk})\\ Y_{ijk} &= \mu + \epsilon_{ijk} \end{align}\]
Dadurch, dass zwei unabhängige Variablen vorhanden sind, können auch zwei verschiedene Abfolgen durchlaufen werden. Nach dem Wegfall des Interaktionseffekts \((\alpha\beta)_{ij}\) kann entweder erst \(\alpha_i\) oder \(\beta_j\) weggelassen werden. Tatsächlich macht die Reihenfolge keinen Unterschied, wenn die Stichprobengröße \(r_i\) in allen Zellen gleich ist. Entsprechend gilt dies nicht mehr, wenn die Stichprobengrößen sich unterscheiden.
Eine Besonderheit die in der Literatur auftauchen kann ist die Modellformulierung in Formel \(\eqref{eq-ed-crfd-additiv}\). D.h. das Modell ohne den Interaktionsfaktor. Dieses Modell kann in manchen Fälle auch das full model sein, wenn davon ausgegangen werden kann, dass keine Interaktionseffekte zwischen den beiden Variablen vorhanden sein können bzw. vorhanden sind. In der Literatur wird dieses Modell als additives Modell bzw. two-way main effects model bezeichnet.
Die statistischen Hypothesen sind wenig überraschend die üblichen mit der Annahme von keinen Effekten unter der \(H_0\) und entsprechend Effekten unter der \(H_1\). Entsprechend ist die Formulierung der \(H_0\)-Hypothesen für die Hauptfaktoren \(A\) und \(B\) bzw. den Interaktionseffekt \(A\times B\):
\[\begin{align*} \alpha_1 &= \alpha_2 = \ldots = \alpha_p = 0\\ \beta_1 &= \beta_2 = \ldots = \beta_q = 0 \\ (\alpha\beta)_{11} &= (\alpha\beta)_{12} = \ldots = (\alpha\beta)_{pq} = 0 \\ \end{align*}\]
bzw. die entsprechenden Alternativhypothesen \(H_1\), dass sich mindestens zwei Faktorstufen \(\alpha_i\) bzw. \(\beta_j\) oder Interaktionskombinationen \((\alpha\beta)_{ij}\) voneinander unterscheiden. Unter dem Ansatz des Modellvergleichs sind die Hypothesen wieder dahingehend zu interpretieren, dass die Hinzunahme bzw. das Weglassen einer Modellkomponente eine statistisch signifikante Verbesserung des Modells nach sich zieht bzw. eben nicht.
Die alternative aber äquivalente Herleitung der Hypothesen im Sinne einer Variananalyse führt zu einer Unterteilung der Gesamtvarianz in einzelne Komponenten auf der Grundlage der verschiedenen Modellkomponenten.
\[\begin{equation} SS_{\text{total}} = SS_{\text{Faktor }A} + SS_{\text{Faktor }B} + SS_{A\times B} + SS_{\text{error}} \label{eq-ed-crfd-sstotal} \end{equation}\]
Es ergibt sich die folgende \(F\)-Tabelle bei einer Zellbesetzung mit \(r\) Replikationen.
| Term | \(df\) | \(SSQ\) | \(MSQ\) | \(F\) |
|---|---|---|---|---|
| Faktor \(A\) | \(p-1\) | \(ssA\) | \(\frac{ssA}{p-1}\) | \(\frac{msA}{msE}\) |
| Faktor \(B\) | \(q-1\) | \(ssB\) | \(\frac{ssB}{q-1}\) | \(\frac{msB}{msE}\) |
| \(AB\) | \((p-1)(q-1)\) | \(ssAB\) | \(\frac{ssAB}{(p-1)(q-1)}\) | \(\frac{msAB}{msE}\) |
| Error | \(n - pq\) | \(ssE\) | \(\frac{ssE}{n-pq}\) |
\(sstot = \sum_{i}\sum_{j}\sum_k y_{ijk}^2 - n\bar{y}_{...}^2\)
\(ssA = qr\sum_i \bar{y}_{i..}^2-n\bar{y}_{...}^2\)
\(ssB = pr\sum_j \bar{y}_{.j.}^2-n\bar{y}_{...}^2\)
\(ssAB = r\sum_i\sum_j \bar{y}_{ij.}^2 - qr\sum_i\bar{y}_{i..}^2 - pr\sum_j\bar{y}_{.j.}^2+n\bar{y}_{...}^2\)
Der Schätzer für \(\sigma^2\) ist wie gewohnt die mittlere Summe \(MSE\) der quadrierten Abweichungen von den jeweiligen Gruppenmittelwerten \(\bar{y}_{ij.}\), also die Residuen \(\hat{\epsilon}_{ijk} = e_{ijk}\).
\[\begin{equation} \hat{\sigma}^2 = MSE = \frac{\sum_i \sum_j \sum_k (y_{ijk} - \bar{y}_{ij.})^2}{N-(pq)} \end{equation}\]
Eine obere Konfidenzintervallgrenze kann abgeschätzt werden mit:
\[\begin{equation} \sigma^2 \leq \frac{ssE}{\chi^2_{n-pq,\alpha}} \end{equation}\]
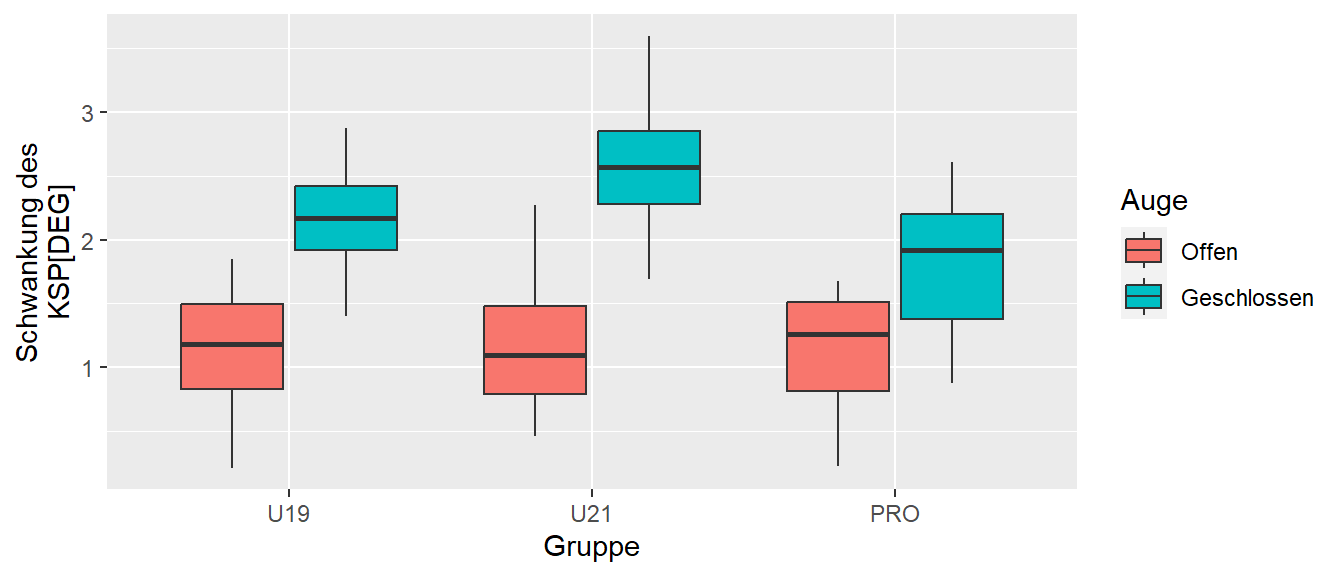
In Abbildung 27.1 ist ein Beispiel adaptiert nach Jadczak u. a. (2019) mit hypothetischen Daten dargestellt.

Es wurde die Gleichgewichtsfähigkeit bei drei verschiedenen Gruppen (Faktor \(A, p = 3\)) unter zwei Konditionen (Faktor \(B, q = 2\)) untersucht. Größere Werte deuten auf eine schlechtere Gleichgewichtsfähigkeit hin. Wie zu erwarten nimmt in allen drei Gruppen die Gleichgewichtsfähigkeit bei geschlossen Augen ab. Allerdings scheint der Unterschied über die drei Gruppen unterschiedlich stark ausgeprägt zu sein. D.h. die Daten deuten auf einen Interaktionseffekt. Um Interaktionseffekte noch einmal besser zu verstehen schauen wir uns im Folgenden verschiedene Arten von Interaktionseffekten und deren Beziehung zu Haupteffekten an.
27.2 Systematik und Problem bei Interaktionseffekten
In Abbildung 27.2 sind beispielhaft die Ergebnisse für ein \(2\times 2\) CRFD abgetragen.
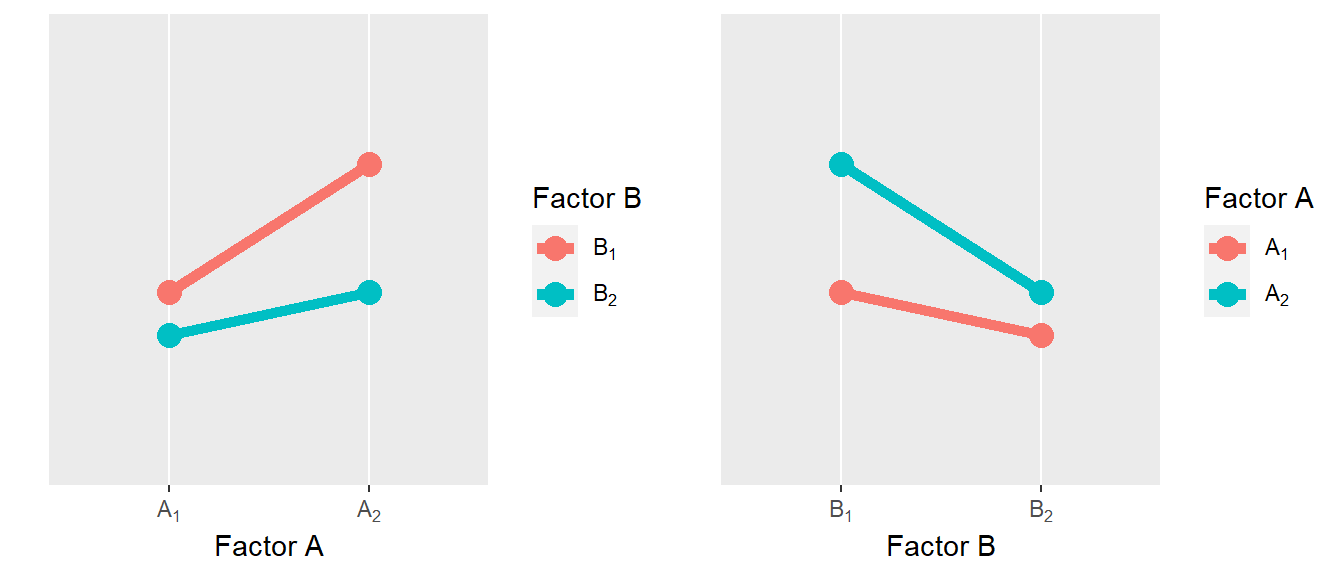
Wir haben zwei Faktoren \(A\) und \(B\) die jeweils zwei Stufen haben \(A_1, A_2\) und \(B_1, B_2\). Um die Beziehung zwischen den Haupteffekten als den Unterschieden zwischen \(A_1\) und \(A_2\) bzw. \(B_1\) und \(B_2\) unabhängige von Wert der jeweils anderern Variable zu interpretieren ist es am einfachsten die Frage zu stellen: “Wenn ich innerhalb eines Faktors von einer Stufe zur nächsten Stufe gehe. Kann ich dann eine einheitliche Aussage treffen?”. Also im Fall Abbildung 27.2 wenn ich von \(A_1\) nach \(A_2\) gehe, dann beobachten wir eine Zunahme der abhängigen Variable unabhängig ob ich mich in Stufe \(B_1\) oder \(B_2\) befinde. Das Gleiche gilt für Hauptfaktor \(B\). Wenn ich von \(B_1\) nach \(B_2\) gehe, dann nimmt in beiden Fällen (\(A_1\) und \(A_2\)) der Wert der abhängigen Variablen ab. D.h. in diesem Fall kann sinnvoll über den Haupteffekt gesprochen werden, trotzdem ein Interaktionseffekt vorliegt, die die Zunahme unter \(A\) bzw. die Abnahme unter \(B\) unterschiedlich ist, je nach dem Wert der jeweils anderen Variable. Wenn die Haupt- und Interkationseffekte dies Form annehmen, dann wird von einem ordinalen Interaktionseffekt gesprochen. D.h. bei einem ordinalen Interaktionseffekt kann auch sinnvoll über die Haupteffekte gesprochen werden.
In Abbildung 27.3 ist nun ein andere Konfiguration der Interaktionseffekte abgebildet.
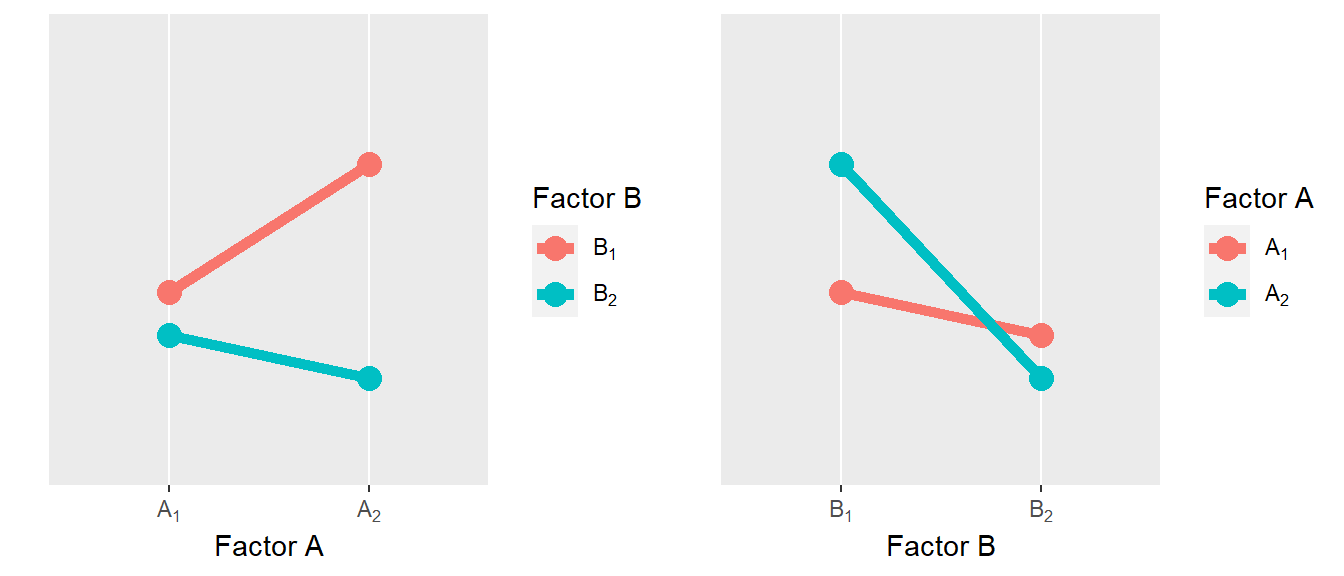
Hier macht die Interpretation der Haupteffekt nur noch im Fall von Faktor \(B\) Sinn, da in beiden Fällen es zu einer Abnahme der Werte der abhängigen Variable kommt. Für Faktor \(A\) dagegen, hängt die Veränderung in der abhängigen Variablen wenn von \(A_1\) nach \(A_2\) gegangen wird, davon ab, ob es Faktor \(B\) den Wert \(B_1\) hat, bei dem e szu einer Zunahme der abhängigen Variable kommt, während es unter \(B_2\) zu einer Abnahme kommt. Diese Art des Interaktionseffekt wird daher als hybrid oder semidisordinaler Interaktionseffekt bezeichnet. D.h. hier können wir nur für Faktor \(B\) sinnvoll über den Haupteffekt sprechen. Allerdings, hängt die Höhe der Abnahme von \(B_1\) nach \(B_2\) von Faktor \(A\) ab.
Wenig überraschend gibt es noch eine weitere Konfiguration von Interaktionseffekten die in Abbildung 27.4 abgebildet sind.
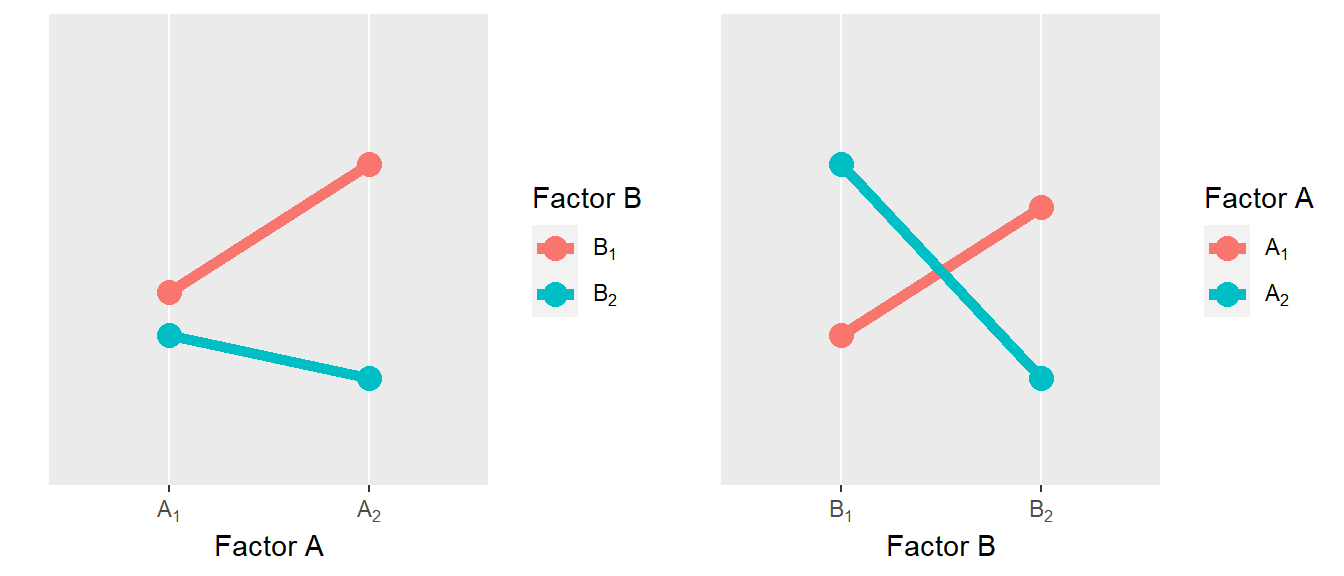
Im disordinalen Fall kann für beide Faktoren nicht sinnvoll über die Hauptfaktoren gesprochen werden, da die Veränderung der abhängigen Variablen jeweils immer von der Kombination der Faktoren abhängig ist.
Tatsächlich ist leider die Einteilung von ordinal, semidisoridnal und disoridnalen Interaktionseffekten selten in realen Experimenten zu beobachten, da oftmals mehr als nur \(2\times 2\) CRFD durchgeführt werden. In Abbildung 27.5 sind mögliche Interaktionseffekte wenn \(p,q > 2\) gilt abgetragen.
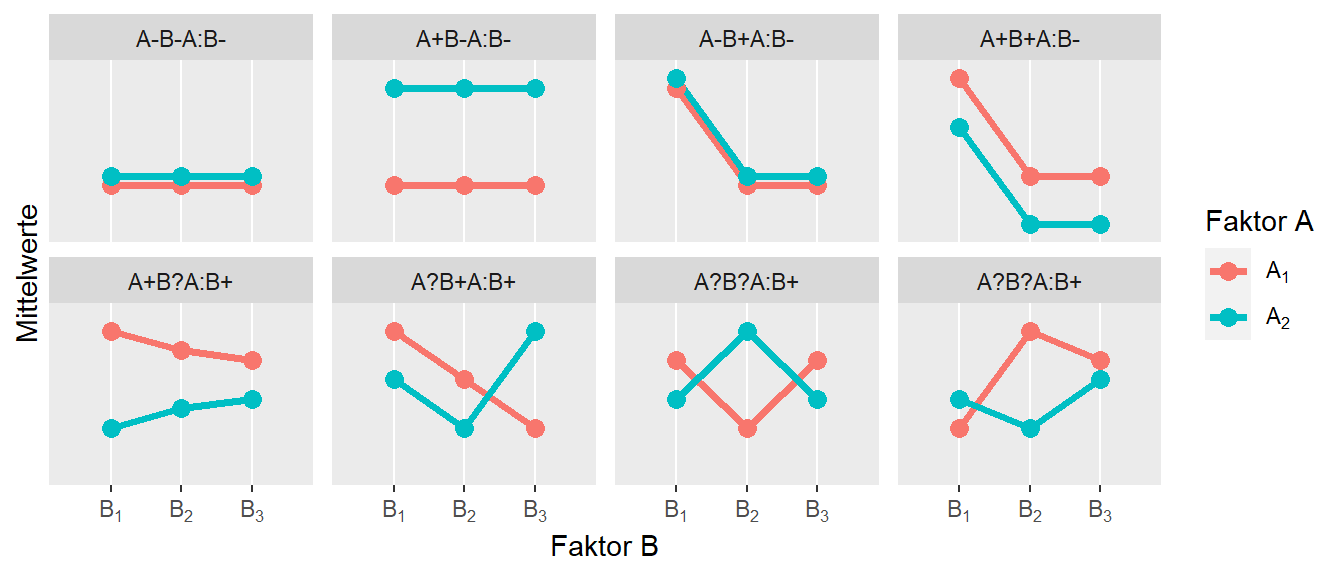
In Abbildung 27.5 ist die Interpretation der Haupteffekte bzw. die Anwesenheit von Interaktionseffekten mit (\(+\)), (\(-\)) und (\(?\)). Hier zeigt sich, dass die mögliche Anordnung von Haupt- und Interaktionseffekten sehr schnell sehr unübersichtlich wird. Daher kann als Faustregel genommen werden. In der ersten Zeile sind keine Interpretationseffekte beteiligt und in diesen Fällen ist die Interpretation der Haupteffekte unproblematisch. In der zweiten Zeile dagegen sind teilweise Interpretation möglich aber müssen immer durch mehrere Qualikationsklauseln begleigtet werden um die Daten korrekt zu interpretieren. Zum Beispiel im zweiten Beispiel von links in der zweiten Reihe, sehen wir eine Abnahme der abhängigen Variablen unter Variable \(B\), allerdings nur wir von \(B_1\) nach \(B_2\) gehen. Daher kann oft die folgende Faustregel angewendet werden.
Wenn Interaktionseffekte vorhanden sind, dann ist die Interpretation von Haupteffekten selten sinnvoll.
Letztendlich ist die Definition eines Interaktionseffekts, dass der Effekt der einen Variablen von der Ausprägung der anderen Variablen abhängt. Dies sollte daher immer Berücksichtigung finden. Denn Beispieln in Abbildung 27.5 folgend ist bei einem CRFD die erstellen eines sogenannten Interaktionsdiagramm sinnvall. Bei dem einfach nur die Mittelwerte gegen die Konditionen der einen Variable und verbundenüber die andere Variable dargestellt werden. In Abbildung 27.6 ist ein Interaktionsdiagramm für die Fußballbalancierdaten abgebildet.
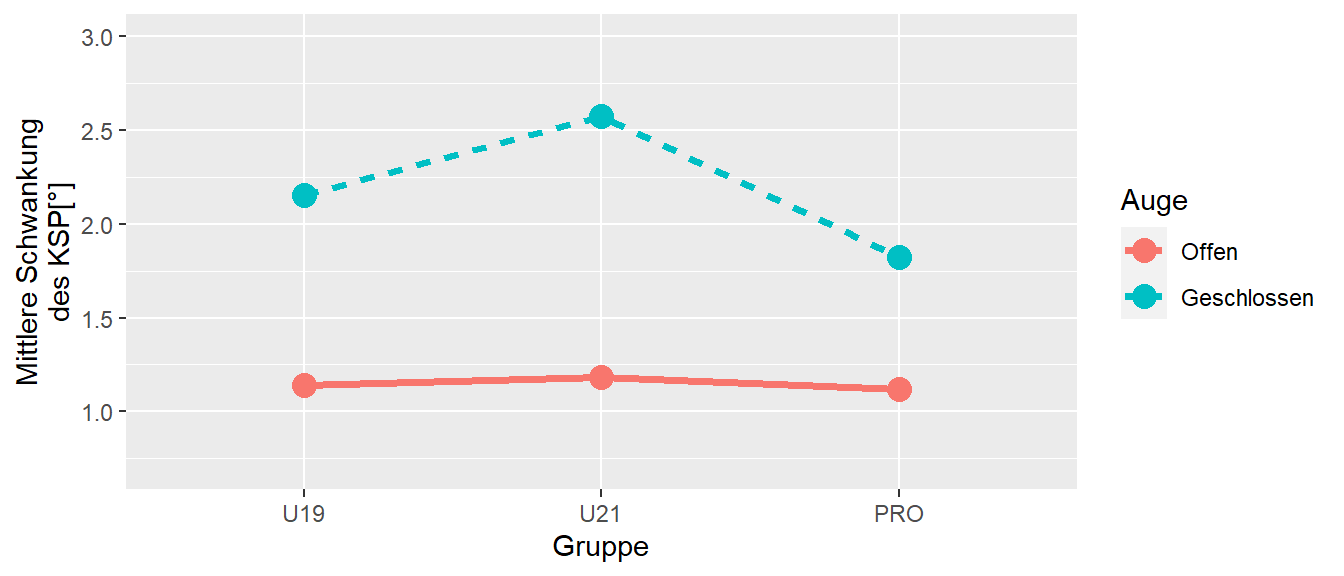
Da das CRFD nicht beschränkt ist auf nur zwei Variablen sondern beliebig weiter ausgeweitet werden kann, sollte allerdings unter dem Gesichtspunkt von interpretierbaren Interaktionseffekten genau überprüft werden wie sinnvoll die Einbeziehung vieler Faktoren ist. Beispielsweise sind bei drei Variablen eben schon Dreifachinteraktionen zu interpretieren zu denen es oft schwierig ist interpretierbare wissenschaftliche Hypothesen bzw. interpretationen zu erstellen.
Allgemein ist dabei zu sagen, dass ein Experiment mit mehreren Faktoren üblicherweise effizienter ist, als mehrere Experimenten bei denen die Faktoren einzeln untersucht werden. Zusätzlich ist eine Analyse von Interaktionseffekten bei mehreren kleinen Experimenten nicht oft nicht möglich.
27.3 Analse eines CRFD in R
Die Analyse von CRFDs in R bringt eigentlich wenig Neues mit sich und kann mit den üblichen Modellbeschreibungen des linearen Modells durchgeführt werden.
Ein Paket das die Erstellung von deskriptive Statistiken sehr stark vereinfacht ist summarytools, bzw. die Funktion descr() aus diesem Paket.
sway |> group_by(Gruppe, Auge) |>
descr(stats = c('mean','med','sd','q1','q3'))| Gruppe | Auge | variable | mean | med | sd | q1 | q3 |
|---|---|---|---|---|---|---|---|
| U19 | Offen | sway | 1.14 | 1.18 | 0.47 | 0.82 | 1.49 |
| U19 | Geschlossen | sway | 2.15 | 2.17 | 0.40 | 1.92 | 2.42 |
| U21 | Offen | sway | 1.18 | 1.09 | 0.48 | 0.78 | 1.48 |
| U21 | Geschlossen | sway | 2.57 | 2.57 | 0.50 | 2.28 | 2.85 |
| PRO | Offen | sway | 1.12 | 1.26 | 0.44 | 0.81 | 1.51 |
| PRO | Geschlossen | sway | 1.82 | 1.92 | 0.53 | 1.38 | 2.20 |
Mittels der lm()-Funktion können wir wie immer über den Modellvergleich gehen.
mod_f <- lm(sway ~ Gruppe * Auge, sway)
mod_r1 <- lm(sway ~ Gruppe + Auge, sway)
mod_r2 <- lm(sway ~ Gruppe, sway)
mod_r3 <- lm(sway ~ 1, sway)
anova(mod_r3, mod_r2, mod_r1, mod_f)Analysis of Variance Table
Model 1: sway ~ 1
Model 2: sway ~ Gruppe
Model 3: sway ~ Gruppe + Auge
Model 4: sway ~ Gruppe * Auge
Res.Df RSS Df Sum of Sq F Pr(>F)
1 149 79.376
2 147 75.201 2 4.175 9.3519 0.0001519 ***
3 146 35.130 1 40.071 179.5070 < 2.2e-16 ***
4 144 32.145 2 2.984 6.6847 0.0016743 **
---
Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1Oder wir verwenden direkt aov() um die \(F\)-Tabelle zu erhalten:
aov() erstellen.
mod_aov <- aov(sway ~ Gruppe * Auge, data = sway)
summary(mod_aov) Df Sum Sq Mean Sq F value Pr(>F)
Gruppe 2 4.18 2.09 9.352 0.000152 ***
Auge 1 40.07 40.07 179.507 < 2e-16 ***
Gruppe:Auge 2 2.98 1.49 6.685 0.001674 **
Residuals 144 32.15 0.22
---
Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1Wie immer wieder betont, bei der Verwendung mit aov() geschieht nichts anderes und es wird lediglich lm() im Hintergrund aufgerufen. So können wir von aov() auch die coef()-Funktion anwenden und erhalten genau die gleichen Steigungskoeffizienten \(\beta_i\) wie bei lm().
cbind(coef(mod_f), coef(mod_aov)) [,1] [,2]
(Intercept) 1.13897248 1.13897248
GruppeU21 0.04505768 0.04505768
GruppePRO -0.01707991 -0.01707991
AugeGeschlossen 1.01075960 1.01075960
GruppeU21:AugeGeschlossen 0.37937763 0.37937763
GruppePRO:AugeGeschlossen -0.31050320 -0.31050320Da es sich bei der Analyse eines CRFD um nichts anderes als um ein lineares Modell handelt, kann der Modellfit wie immer über die uns schon bekannten Methoden mittels der Residuen untersucht werden.
Den Levene-Test können wir ebenfalls wie beim CRD anwenden.
car::leveneTest(mod_aov)Levene's Test for Homogeneity of Variance (center = median)
Df F value Pr(>F)
group 5 0.6544 0.6586
144 Die \(H_0\)-Hypothese des Levene-Tests ist die Varianzgleichheit, d.h. alle Faktorkombinationen haben die gleiche Varianz. Da der Test als Voraussetzungstest eingesetzt wird, setzen wir die Irrtumswahrscheinlichkeit wieder mit \(\alpha = 0.1\) an. Dementsprechend wird im vorliegenen Fall die \(H_0\) nicht abgelehnt und die Annahme der Varianzgleichheit beibehalten.
27.4 Effektstärken im CRFD
Natürlich kann für ein CRFD ebenfalls eine Effektstärke wie für ein CRD berechnet werden. Hier gilt hier genauso, dass keine eins-zu-eins Abbildung der Effektstärke auf eine spezifische Anordnung der Stufenmittelwerte gegeneinander \(\bar{y}_{ij.}\) besteht. Verschiedene Abweichungen der Mittelwerte gegeneinander können zu der gleichen Effektstärke führen. Ein weiterer Punkt, der die Bestimmung von Effektstärken beim CRFD verkompliziert beruht darauf, dass unterschiedliche Arten möglich sind die Residualvarianz zu bestimmen. Ausgangspunkt ist noch einmal die Effektstärke \(f\) im CRD. Im CRD ist die Effektstärke \(f\) auf der Basis des Modellansatzes, dass die Effektvarianz durch die Fehlervarianz geteilt wird, bzw. die kalibiert wird. Eine gegebene Effektvarianz \(\sigma_{\text{Effekt}}^2\) führt zu einer größeren Effektstärke wenn die Fehlervarianz \(\sigma_{\epsilon}^2\) kleiner ist und umgekehrt wenn die Fehlervarianz größer ist.
\[\begin{equation*} f = \frac{\sigma_{\text{Effekt}}^2}{\sigma_{\epsilon}^2} \end{equation*}\]
Im CRFD besteht allerdings die Möglichkeit die Fehlervarianz \(\sigma_{\epsilon}^2\) auf unterschiedliche Arten zu bestimmen. Vergleichen wir dazu einmal zwei Modelle. Ein volles Modell mit zwei Faktoren \(A\) und \(B\) und ein reduziertes Modell mit nur dem Faktor \(A\).
\[\begin{align} y_{ijk} &= \mu + \alpha_j + \beta_k + (\alpha\beta)_{jk} + \epsilon_{ijk} \\ y_{ij} &= \mu + \alpha_j + \epsilon_{ij} \\ \end{align}\]
Es soll die Effektstärke für den Faktor \(A\) bestimmt werden. Wenn wir die beiden Modell in Bezug auf die Varianzkomponenten aufschreiben, erhalten wie bereits oben beschrieben für das volle Modell:
\[\begin{equation} \sigma_y^2 = \sigma_{\alpha}^2 + \sigma_{\beta}^2 + \sigma_{(\alpha\beta)}^2 + \sigma_{\epsilon(full)}^2 \end{equation}\]
Entsprechend für das reduzierte Modell:
\[\begin{equation} \sigma_y^2 = \sigma_{\alpha}^2 + \sigma_{\epsilon(reduced)}^2 \end{equation}\]
Dementsprechend ist der Zähler \(\sigma_{\alpha}^2\) in beiden Fällen gleich, aber der Nenner \(\sigma_{\epsilon}\) wird sich unterscheiden, da \(\sigma_{\epsilon(full)}^2 \neq \sigma_{\epsilon(reduced)}^2\) gilt. Warum ist das so? Im reduzierten Modell, wird die Varianz die auf Grund des Faktors \(B\) also \(\sigma_{\beta}^2\) und der Interaktion \(A:B\) also \(\sigma_{(\alpha\beta)}^2\) entsteht nicht modelliert. Die Varianz ist aber immer noch vorhanden und wandert dadurch in den Fehlerterm \(\sigma_{\epsilon(reduced)}^2\). Daher gilt:
\[\begin{equation*} \sigma_{\epsilon(full)}^2 \leq \sigma_{\epsilon(reduced)}^2 \end{equation*}\]
In Bezug auf die Residualvarianz für den Faktor \(A\) gilt:
\[\begin{equation*} \sigma_{\epsilon(full)}^2 + \sigma_{\beta}^2 + \sigma_{(\alpha\beta)}^2 = \sigma_{\epsilon(reduced)}^2 \end{equation*}\]
Dies wiederum führt dazu je nachdem durch welche Residualvarianz die Effektvarianz \(\sigma_{\text{Effekt}}^2\) geteilt wird, die Effektstärke entweder größer oder kleiner wird. Wird die Residualvarianz \(\sigma_{\epsilon(full)}^2\) verwendet, wird entsprechend ein größeren Effekt bestimmen als wenn \(\sigma_{\epsilon(reduced)}^2\) verwendet wird. Im ersten Fall, wenn die kleiner Residualvarianz verwendet wird, wird die Effektstärke als partial bezeichnet. D.h. anhand des vollen Modells können zwei verschiedene Arten von Effektstärken bestimmen werden.
\[\begin{align*} f &= \frac{\sigma_{\alpha}^2}{\sigma_{\beta}^2 + \sigma_{(\alpha\beta)}^2 + \sigma_{\epsilon}^2} \\ f_{\text{partial}} &= \frac{\sigma_{\alpha}^2}{\sigma_{\epsilon}^2} \\ \end{align*}\]
Diese Formeln sind dabei nur konzeptionell zu verstehen und wir bestimmen die beiden Formeln wieder mittels einer \(\omega^2\)-Effektstärke.
\[\begin{align*} \hat{\omega}^2 &= \frac{ss\text{Eff}-df_{\text{Eff}}\cdot MSE}{ssT+MSE} \\ &= \frac{df\text{Eff} \cdot (F_{\text{Effekt}})-1)}{\sum_{\text{alle Effekte}}(df_{\text{Eff}_i} F_{\text{Eff}_i}) + dfE + 1} \end{align*}\]
\[\begin{align*} \hat{\omega}_{\text{partial}}^2 &= \frac{SS_{\text{effect}}-df_{\text{effect}}MS_W}{SS_{\text{effect}}+(N-df_{\text{effect}})MS_W} \\ &= \frac{df_{\text{effect}}(F_{\text{effect}})-1)}{df_{\text{effect}}(F_{\text{effect}}-1)+N} \end{align*}\]
D.h. es werden für alle drei Modellterm \(A\), \(B\) und \(A:B\) jeweils Effektstärken bestimmet. Entsprechend können weitere Effektstärken bestimmt werden, wenn mehr als zwei Faktoren im Modell verwendet werden.
Die Einordnung der Effektstärken ist wieder die gleiche wie bereits im Rahmen des CRD eingeführt.
| \(\omega^2\) | |
|---|---|
| klein | 0.01 |
| mittel | 0.06 |
| groß | 0.14 |
Die Interpretation der Effektstärke nach Tabelle 27.3 ist genauso willkürlich wie die Irrtumswahrscheinlichkeit von \(\alpha = 0.05\)!
Beispiel 27.1 In Listing 27.1 haben wir die \(F\)-Tabelle für die Fußballdaten berechnet und nun möchten wir die Effektstärke \(\omega^2\) für den Effekt der Gruppe bestimmen. Dazu extrahieren wir die benötigten Komponenten aus der Tabelle um \(\omega^2\) zu bestimmen.
ssEff <- 4.18
dfEff <- 2
ssT <- 4.18 + 40.07 + 2.98 + 32.15
MSE <- 0.22
omega_sqr_gruppe <- (ssEff - dfEff * MSE)/(ssT + MSE)
omega_sqr_gruppe[1] 0.04698492D.h bei dem Einfluss der Gruppe handelt es sich um eine mittlere Effektstärke.
In der Literatur werden in den meisten Fällen die partiellen Effektstärken angegeben. Allerdings erscheint dies wenig sinnvoll, da die Effekstärke dann eine Funktion des Untersuchungsdesings ist. Schauen wir uns ein hypothetisches Beispiel dazu an. Sei zum Beispiel eine Untersuchung durchgeführt worden um den Einfluss von zwei Instruktionsmethoden (Faktor \(A\)) zu vergleichen. Die Verarbeitung der Instruktion ist aber gleichzeitig eine Funktion von bestimmten kognitiven Prädispositionen (Faktor \(B\)) die mittels eines umfangreichen Fragebogen ermittelt werden müssen. Bei der Studie wird ein Effekt für bei beide Faktoren und deren Interaktion gefunden. Die partiellen Effektstärken werden dokumentiert. In einer Nachfolgestudie soll der Effekt der Instruktionen noch einmal reproduziert werden. Allerdings sind nicht ausreichend Resourcen vorhanden um den Fragebogen durchzuführen. Basierend auf den Effektstärken für den Faktor \(A\) aus der vorhergehenden Studie wird die Stichprobengröße bestimmt. Dies führt jetzt allerdings dazu, dass die nominale Power der Studie geringer ist, da die Effekstärke überschätzt wird, da die Varianz auf Grund der kognitiven Prädisposition in die Fehlervarianz wandert. Daher ist insgesamt die Dokumentation der normalen Effektstärke in den meisten Fällen sinnvoller wenn nicht einfach beide angegeben werden.
27.4.1 Effektstärken \(\omega^2\) und \(\omega_{\text{partial}}^2\) in R
In R kann, nachdem das Modell mit lm() gefittet wurde, mittels der Funktion omega_squared() aus dem Paket effectsize die Effektstärken bestimmen werden. omega_squared() hat einen Parameter partial der festlelgt ob die normale Effektstärke oder die partielle Effektstärke berechnet wird. Wird der Parameter auf FALSE gesetzt, werden die normalen Effektstärken bestimmt.
effectsize::omega_squared(mod_aov, partial=FALSE, ci=0.95)# Effect Size for ANOVA (Type I)
Parameter | Omega2 | 95% CI
-----------------------------------
Gruppe | 0.05 | [0.00, 1.00]
Auge | 0.50 | [0.41, 1.00]
Gruppe:Auge | 0.03 | [0.00, 1.00]
- One-sided CIs: upper bound fixed at [1.00].Entsprechend berechnet omega_squared() mit partial=TRUE die partiellen Effektstärke die leider auch standardmäßig eingestellt ist.
effectsize::omega_squared(mod_aov, partial=TRUE, ci=0.95)# Effect Size for ANOVA (Type I)
Parameter | Omega2 (partial) | 95% CI
---------------------------------------------
Gruppe | 0.10 | [0.03, 1.00]
Auge | 0.54 | [0.46, 1.00]
Gruppe:Auge | 0.07 | [0.01, 1.00]
- One-sided CIs: upper bound fixed at [1.00].Bei der Dokumentation der Effektstärke sollte wie immer auch das Konfidenzintervall angegeben werden, was in der Literatur leider auch oft nicht gemacht wird.
27.5 Mehrfachvergleiche im CRFD
Im CRFD können wir genauso wie auch im CRD Mehrfachvergleiche verwenden um gezielt Unterschiede zwischen bestimmten Kombination der Faktorstufen zu untersuchen. Prinzipiell laufen die Mehrfachvergleiche daher genauso wie im CRD ab. Es werden ein Kontrast und die dazugehörende Varianz berechnet und das Verhältnis mit einem kritischen Werten \(w\) verglichen. Wiederum in Abhängigkeit davon welche Methode verwendet wird ändert sich entsprechend der kritische Wert \(w\).
Durch die Interaktionseffekt ergbit sich jedoch wiederum ein zusätzlicher Punkt beim Interaktionsmodell der beachtet werden sollte. Nämlich, nicht immer sind alle algebraisch möglichen Vergleiche auch tatsächlich inhaltlich sinnvoll. Im Bespiel mit den Fußballdaten sind in Abbildung 27.7 noch einmal die Mittelwerte der verschiedenen Gruppen abgetragen.

Prinzipiell können immer alle Gruppenmittelwerte des Modells miteinander paarweise verglichen werden bzw. alle weiteren komplexen Kontraste berechnet werden. Bei der Beschränkung auf die paarweisen Vergleiche, wird in diesem konkreten Fall beispielsweise der Vergleich zwischen den Werten der U19 bei geschlossenen Augen mit den PROs bei offenen Augen inhaltlichen wenig Sinn machen. Zumindest ist es nicht direkt ersichtlich welche Art von wissenschaftlicher Hypothese a-priori formuliert werden könnte, die genau diesen Vergleich zum Ziel hat. Anders ist beispielsweise der Vergleich zwischen den Augenkondition innerhalb der PRO-Spieler. Daher ist in den meisten Fällen nur eine Untermenge der möglichen paarweisen Vergleich inhaltlich auch wirklich sinnvoll. Aus Gründen der Power sollte daher die Analyse auch möglichst nur auf diese Teilmenge beschränkt werden. In Abbildung 27.8 sind die wahrscheinlich sinnvollen Vergleiche für das Beispiel eingezeichnet.
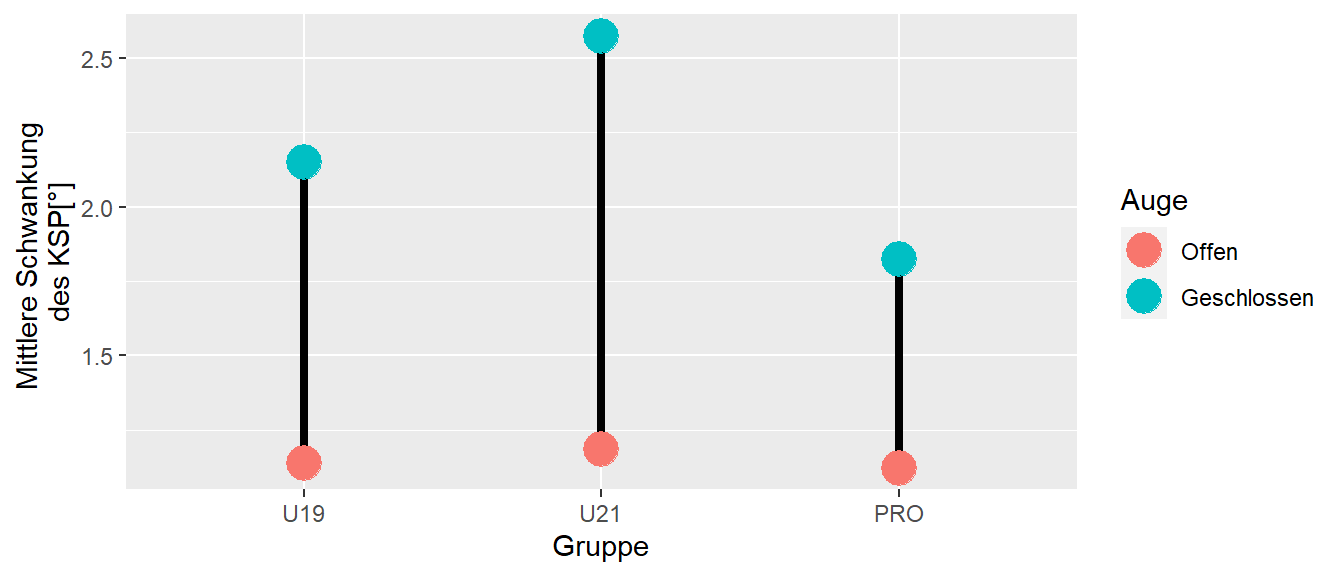
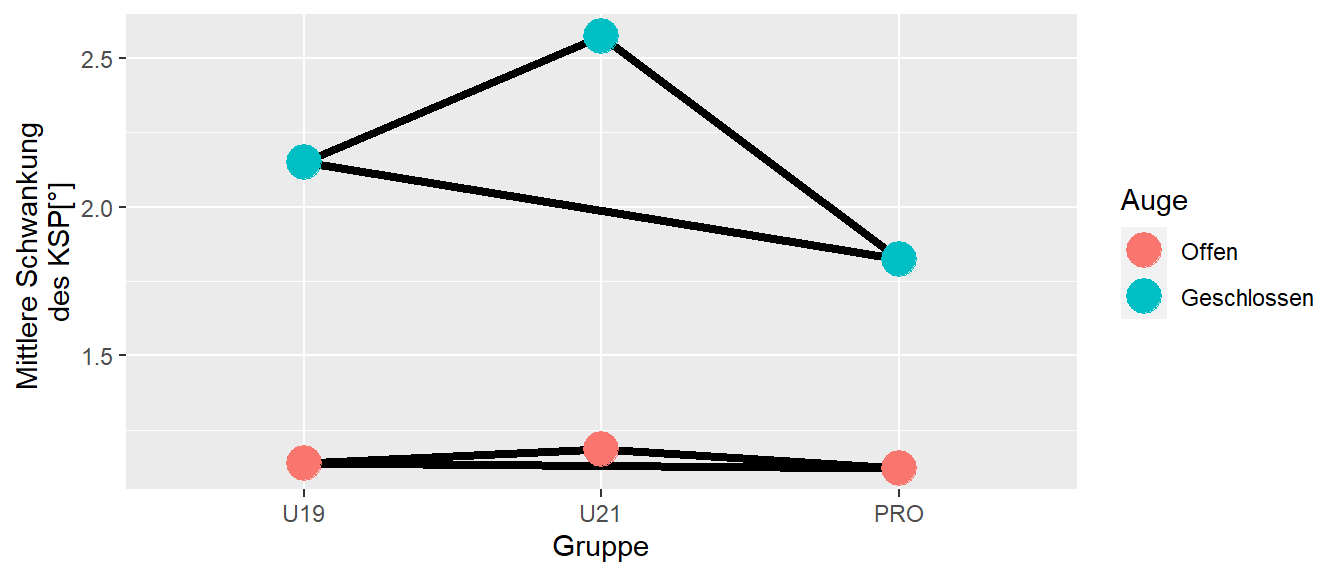
Für den vorliegenden Fall, sind daher die Unterschied zwischen den Gruppen getrennt für die beiden Augenkonditionen bzw. der Unterschied zwischen den beiden Augenkonditionen für jede Gruppe getrennt sinnvoll. D.h. es werden insgesamt neuen verschiedene paarweise Vergleichen betrachtet im Gegensatz zu den 15 möglichen. Wir beispielsweise die Bonferonni-Korrektur angewendet bedeutet dies schon einen Unterschied ob \(0.05/9 = 0.006\) oder \(0.05/15 = 0.003\) für \(\alpha\) angesetzt muss. Schauen wir uns direkt an, wie dei Mehrfachvergleiche in R durchgeführt werden.
27.6 Mehrfachvergleiche in R
In R läuft der Vergleich wiederum nach dem bekannten Muster ab. Zunächst werden die Modellmittelwerte mittels der emmeans()-Funktion berechnet. Anschließend kann dann mittels der pairs() bzw. der contrast()-Funktion der gewünschte Vergleich durchgeführt werden. Allerdings, da emmeans() extrem flexibel ist, gibt es immer mehrere Arten um zum gleichen Ergebnis zu kommen.
Fangen wir erst einmal mit allen möglichen Vergleichen an. Wir fitten zunächst alle Gruppenmittelwertskombination mit emmeans().
mod_em <- emmeans(mod_aov, ~Gruppe*Auge)
mod_em Gruppe Auge emmean SE df lower.CL upper.CL
U19 Offen 1.14 0.0945 144 0.952 1.33
U21 Offen 1.18 0.0945 144 0.997 1.37
PRO Offen 1.12 0.0945 144 0.935 1.31
U19 Geschlossen 2.15 0.0945 144 1.963 2.34
U21 Geschlossen 2.57 0.0945 144 2.387 2.76
PRO Geschlossen 1.82 0.0945 144 1.635 2.01
Confidence level used: 0.95 Im nächsten Schritt berechnen wir nun alle paarweisen Vergleiche entweder mit pairs() oder mit contrast(method = "pairwise"). Nehmen wir pairs().
pairs(mod_em) contrast estimate SE df t.ratio p.value
U19 Offen - U21 Offen -0.0451 0.134 144 -0.337 0.9994
U19 Offen - PRO Offen 0.0171 0.134 144 0.128 1.0000
U19 Offen - U19 Geschlossen -1.0108 0.134 144 -7.564 <.0001
U19 Offen - U21 Geschlossen -1.4352 0.134 144 -10.740 <.0001
U19 Offen - PRO Geschlossen -0.6832 0.134 144 -5.112 <.0001
U21 Offen - PRO Offen 0.0621 0.134 144 0.465 0.9972
U21 Offen - U19 Geschlossen -0.9657 0.134 144 -7.226 <.0001
U21 Offen - U21 Geschlossen -1.3901 0.134 144 -10.402 <.0001
U21 Offen - PRO Geschlossen -0.6381 0.134 144 -4.775 0.0001
PRO Offen - U19 Geschlossen -1.0278 0.134 144 -7.691 <.0001
PRO Offen - U21 Geschlossen -1.4523 0.134 144 -10.867 <.0001
PRO Offen - PRO Geschlossen -0.7003 0.134 144 -5.240 <.0001
U19 Geschlossen - U21 Geschlossen -0.4244 0.134 144 -3.176 0.0221
U19 Geschlossen - PRO Geschlossen 0.3276 0.134 144 2.451 0.1460
U21 Geschlossen - PRO Geschlossen 0.7520 0.134 144 5.627 <.0001
P value adjustment: tukey method for comparing a family of 6 estimates Hier erhalten wir alle Vergleiche, also auch diejenigen die inhaltlich weniger sinnvoll sind. Wollen wir uns nur auf die Vergleiche innerhalb der jeweiligen Haupteffekte kontrolliert für die jeweilige Stufe des anderen Effekts beschränken. Können wir den Parameter simple = "each" verwenden.
pairs(mod_em, simple = "each")$`simple contrasts for Gruppe`
Auge = Offen:
contrast estimate SE df t.ratio p.value
U19 - U21 -0.0451 0.134 144 -0.337 0.9393
U19 - PRO 0.0171 0.134 144 0.128 0.9910
U21 - PRO 0.0621 0.134 144 0.465 0.8878
Auge = Geschlossen:
contrast estimate SE df t.ratio p.value
U19 - U21 -0.4244 0.134 144 -3.176 0.0052
U19 - PRO 0.3276 0.134 144 2.451 0.0406
U21 - PRO 0.7520 0.134 144 5.627 <.0001
P value adjustment: tukey method for comparing a family of 3 estimates
$`simple contrasts for Auge`
Gruppe = U19:
contrast estimate SE df t.ratio p.value
Offen - Geschlossen -1.01 0.134 144 -7.564 <.0001
Gruppe = U21:
contrast estimate SE df t.ratio p.value
Offen - Geschlossen -1.39 0.134 144 -10.402 <.0001
Gruppe = PRO:
contrast estimate SE df t.ratio p.value
Offen - Geschlossen -0.70 0.134 144 -5.240 <.0001Alternativ können wir auch direkt die marginalen Mittelwerte berechnen. Zunächst berechnen wir wieder die Mittelwerte mittels emmeans() die Mittelwert für die Stufen über die Gruppen kontrolliert für Kondition der Augen.
mod_em_cauge <- emmeans(mod_aov, ~Gruppe|Auge)
mod_em_caugeAuge = Offen:
Gruppe emmean SE df lower.CL upper.CL
U19 1.14 0.0945 144 0.952 1.33
U21 1.18 0.0945 144 0.997 1.37
PRO 1.12 0.0945 144 0.935 1.31
Auge = Geschlossen:
Gruppe emmean SE df lower.CL upper.CL
U19 2.15 0.0945 144 1.963 2.34
U21 2.57 0.0945 144 2.387 2.76
PRO 1.82 0.0945 144 1.635 2.01
Confidence level used: 0.95 Die Formel ~Gruppe|Auge als zweiter Parameter zu emmeans() bedeutet, dass die Unterschiede zwischen den Stufen für Gruppe geblockt nach den Auge-Konditionen berechnet werden sollen. Alternativ könnte auch die folgende Syntax mit dem Parameter by verwendet werden:
emmeans(mod_aov, ~Gruppe, by = "Auge")Auge = Offen:
Gruppe emmean SE df lower.CL upper.CL
U19 1.14 0.0945 144 0.952 1.33
U21 1.18 0.0945 144 0.997 1.37
PRO 1.12 0.0945 144 0.935 1.31
Auge = Geschlossen:
Gruppe emmean SE df lower.CL upper.CL
U19 2.15 0.0945 144 1.963 2.34
U21 2.57 0.0945 144 2.387 2.76
PRO 1.82 0.0945 144 1.635 2.01
Confidence level used: 0.95 In beiden Fällen erhalten wir die gleichen Modellmittelwerte. Die berechneten Mittelwerte unterscheiden sich dabei nicht zudenjenigen die wir über den ersten Ansatz berechnet haben. Es wird lediglich die strukturelle Unterteilung mit berücksichtigt. Im nächsten Schritt wird wieder die pairs()-Funktion auf die Mittelwerte angewendet, beispielsweise wenn die Bonferroni-Korrektur anwenden möchten.
pairs(mod_em_cauge, adjust = 'bonferroni')Auge = Offen:
contrast estimate SE df t.ratio p.value
U19 - U21 -0.0451 0.134 144 -0.337 1.0000
U19 - PRO 0.0171 0.134 144 0.128 1.0000
U21 - PRO 0.0621 0.134 144 0.465 1.0000
Auge = Geschlossen:
contrast estimate SE df t.ratio p.value
U19 - U21 -0.4244 0.134 144 -3.176 0.0055
U19 - PRO 0.3276 0.134 144 2.451 0.0463
U21 - PRO 0.7520 0.134 144 5.627 <.0001
P value adjustment: bonferroni method for 3 tests Mit der contrast()-Funktion hätte auch alternativ für unstrukturierten Mittelwerte `contrast(mod_em, method=‘pairwise’ simple=‘Auge’) verwendet werden. Die Berechnung der Unterschiede zwischen den Augenstufen geblockt nach Gruppen erfolgt dann genau gleich. Eine Überlegung die notwendig ist, bezieht sich auf die Ebene auf der die Korrektur angewendet wird. Beispielweise, da wir zwei Mehrfachvergleiche durchführen wollen, sollten wir die \(\alpha\)-Level für die beiden Gruppen von Mehrfachvergleichen so anpassen, dass wir insgesamt unter den anvisiertem \(\alpha\) bleiben. In diesem Fall also \(\alpha/2\). Insgesamt, zeigen die Berechnungen im Beispiel, dass zwischen den Gruppen bei offenen Augen keine Unterschiede gefunden wurden, während bei geschlossenen Augen alle Unterschiede statistisch signifikant sind.
27.6.1 Cohen’s d für Mehrfachvergleiche
Cohen’s d-artige Effektstärken können wieder mit der Funktion eff_size() berechnet werden. Hier müssen wieder die Standardabweichung \(\hat{sigma}\) und die Freiheitsgrade direkt angegeben werden. In diesem Fall können diese Werte wieder mit den Funktionen sigma() und df.residual() aus dem Modellfit extrahiert werden.
eff_size(mod_em_cauge,
sigma=sigma(mod_aov),
edf=df.residual(mod_aov))Auge = Offen:
contrast effect.size SE df lower.CL upper.CL
U19 - U21 -0.0954 0.283 144 -0.655 0.464
U19 - PRO 0.0362 0.283 144 -0.523 0.595
U21 - PRO 0.1315 0.283 144 -0.428 0.691
Auge = Geschlossen:
contrast effect.size SE df lower.CL upper.CL
U19 - U21 -0.8983 0.288 144 -1.467 -0.330
U19 - PRO 0.6933 0.286 144 0.128 1.258
U21 - PRO 1.5917 0.298 144 1.003 2.181
sigma used for effect sizes: 0.4725
Confidence level used: 0.95 oder über:
eff_size(mod_em,
sigma=sigma(mod_aov),
edf=df.residual(mod_aov),
simple = "Gruppe")Auge = Offen:
contrast effect.size SE df lower.CL upper.CL
U19 - U21 -0.0954 0.283 144 -0.655 0.464
U19 - PRO 0.0362 0.283 144 -0.523 0.595
U21 - PRO 0.1315 0.283 144 -0.428 0.691
Auge = Geschlossen:
contrast effect.size SE df lower.CL upper.CL
U19 - U21 -0.8983 0.288 144 -1.467 -0.330
U19 - PRO 0.6933 0.286 144 0.128 1.258
U21 - PRO 1.5917 0.298 144 1.003 2.181
sigma used for effect sizes: 0.4725
Confidence level used: 0.95 Leider funktioniert der Parameter simple = "each" nicht mit eff_size(), d.h. wenn die unstrukturierten Gruppenmittelwerte verwendet werden, muss die Funktion zweimal aufgerufen werden, entsprechend mit simple = "Gruppe" bzw. simple = "Auge".
27.7 Anzahl der Replikationen a-priori ermitteln
Wir haben wie immer drei verschiedene Ansätze die Anzahl der Replikationen vor dem Experiment zu bestimmen:
- Anhand der Literatur wird \(f\) bestimmt.
- Es wird ein relevantes/plausibels \(\Delta\), als der Unterschied zwischen zwei Gruppen angesetzt.
- Konfidenzintervalle
Im ersten Fall gibt es zunächst nichts zu berechnen, sondern die Effektstärke für den gewünschten Effekte (Haupt- oder Interaktionseffekt) wird mittels der Literatur hergeleitet.
Im zweiten Fall wird die Effektstärke \(f\) mittels Vorüberlegungen über relevante Unterschiede \(\Delta\) zwischen Faktorstufen festgelegt wie das auch für das CRD durchgeführt wurde. Allerdings ist hierfür immer noch Information über die zu erwartende Streuung der Werte \(\sigma^2\) anhand der Literatur oder einer sonstigen Abschätzung notwendig. Die Effektstärke \(f\) kann dann über die folgende Formel abgeschätzt werden.
\[\begin{equation} f = \sqrt{\frac{\Delta^2}{2(k+1)\sigma^2}} \end{equation}\]
Der Faktor \(k\) gibt dabei die Anzahl der Freiheitsgrade für den jeweiligen Effekt an. Ändert sich dementsprechend ob es sich um einen Interaktions- oder einen Haupteffekt handelt.
Der Replikationsfaktor kann dann über den notwendigen \(F\)-Test ermittelt werden. D.h. wir müssen Tabelle 27.2 , insbesondere die Freiheitsgrade für die verschiedenen Tests, im Blick behalten. Für die beiden Faktoren \(A\) und \(B\) berechnen sich die Freiheitsgrade entsprechend mittels der Anzahl der Faktorstufen \(-1, df_A = p-1, df_B = q-1\), wenn \(p\) die Anzahl der Faktorstufen für Faktor \(A\) und \(q\) die Anzahl der Faktorstufen für Faktor \(B\) definieren. Für den Interaktionseffekt gilt für die Freiheitsgrade \(df_{A\times B} = (p-1)(q-1)\) und für die Residuen \(df_e = N-pq\) mit \(N\) der Gesamtstichprobengröße. \(F\)-Test beruht auf einem Bruch zwischen den Quadratsummen für den Effekt geteilt durch die Quadratsumme der Residuen. Dementsprechend brauchen wir für die Bestimmung des Replikationsfaktors die Anzahl der Faktorstufen und die Gesamtanzahl für einen gegebenen Effekt.
\[\begin{equation*} \text{F-Test: }F = \frac{SS_{\text{Effekt}}}{SS_{\text{Residuen}}} \end{equation*}\]
Die Berechnung efolgt nun über die Effektstärke \(f\) die uns erlaubt den Nonzentralitätsparameter \(\lambda\) zu bestimmen und die Anzahl der Stufen für die wir uns interessieren. Wollen wir zum Beispiel den Replikationsfaktor für einen Haupteffekt mit drei Stufen und \(f = 0.1\) bestimmen. Dann suchen wir diejenigen Freiheitsgrade \(df_e\) für eine gegebene Power und ein gegebenes \(\alpha\)-Niveau. Damit wir nicht zwischen \(f\) und \(lambda\) hin- und herrechnen müssen und Werte vergleichen verwenden wir direkt die Funktion pwr.f2.test() aus dem pwr-package. Die Funktion verwendet nicht \(f\) sondern \(f^2\). Mit der Funktion erhalten wir die Freiheitsgrade für die Residuen und können dann über die Umformung:
\[\begin{equation*} df_{e} = N-qp \Leftrightarrow N = df_{e} + qp \end{equation*}\]
Die Gesamtstichprobengröße.
Beispiel 27.2 Gehen wir beispielsweise von einer Effektstärke in einem \(2\times 3\) Design für den Interaktionseffekt von \(\omega^2 = 0.3\) aus. Zunächst muss \(\omega^2\) in \(f = \sqrt{\omega^2/(1-\omega^2)} = \sqrt{0.3/0.7} = 0.42\) umgerechnet werden. Die Freiheitsgrade für den Interaktionseffekt sind nach Tabelle 27.2 \(df_{A\times B} = (q-1) \times (p-1) = 1 \times 2 = 2\). Unter Verwendung der pwr.f2.test()-Funktion erhalten wir für \(\alpha=0.05\) und power \(0.8\):
pwr::pwr.f2.test(f2 = 0.42**2,
sig.level = 0.05,
power = 0.8,
u = 2)
Multiple regression power calculation
u = 2
v = 54.72222
f2 = 0.1764
sig.level = 0.05
power = 0.8D.h. aufgerundet sind die Freiheitsgrade \(df_e\) für die Quadratsumme der Residuen \(df_e = 55\). Diese Freiheitsgrade stellen wir nun um, um \(N\) berechnen:
\[\begin{equation*} N = df_e + p\cdot q = 55 + 3\cdot 2 = 61 \end{equation*}\]
Da wir bei einem \(2\times 3\)-Design insgesamt sechs Zellen haben aber \(61\) nicht durch \(6\) teilbar ist runden wir auf insgesamt \(N = 66\) auf. D.h. wir benötigen einen Replikationsfaktor von \(11\) für jede Kombination der Faktorstufen und insgesamt somit \(66\) EUs.
Insgesamt zeigt dies, dass die Anzahl der Replikation sich unterscheiden kann, je nachdem ob für ein Design die Power nach den Haupteffekten oder den Interaktionseffekten berechnet wird.
27.8 Nochmal Interaktionseffekte und Power
Es der eben gezeigten Berechnung des Replikationsfaktors ergibt sich noch ein wichtiger Punkt auf den noch mal gesondert eigegangen wird. Schauen wir uns einmal was passiert wenn wir uns die Stichprobengrößen bei einem \(4 \times 3\)-Design anschauen. Gehen wir weiter davon aus, dann die Effektstärke für alle drei Effekte gleich große sind und mit \(f = 0.25\) von mittlerer Größe. Wenn wir die Berechnungen von eben für alle drei Effekt ausführen ergibt sich die folgende Tabelle für die resultierende Anzahl von EUs (siehe Tabelle 27.4).
| Effekt | Freiheitsgrade | \(N\) |
|---|---|---|
| \(A\) | \(4-1=3\) | \(174+12=186\) |
| \(B\) | \(3-1=2\) | \(154+12=166\) |
| \(A \times B\) | \((4-1)(3-1)=6\) | \(217+12=229\) |
Wie in Tabelle 27.4 ersichtlich, steigt die benötigte Stichprobengröße mit der Anzahl der Stufen und insbesondere für die Interaktionseffekte steigt die Anzahl noch mal stark an, trotzdem für alle Effekte die gleiche Effektstärke \(f\) angesetzt wurde. Versuchen wir den Mechanismus einmal heuristisch zu verstehen.
Beim CRD haben wir gesehen, dass der Standardfehler des Haupteffekts für paarweise Vergleiche wie folgt berechnet werden kann. \(N\) ist die Gesamtzahl der EUs in den beiden beteiligten Mittelwerten.
\[\begin{equation*} \sigma_{\text{Haupteffekt}} = \sqrt{\frac{\sigma^2}{N/2} + \frac{\sigma^2}{N/2}} = \frac{2\sigma}{\sqrt{N}} \end{equation*}\]
Der Interaktionseffekt berechnet sich über die Vergleiche von vier Faktorstufen gleichzeitig, da die \(H_0\)-Hypothese die folgende Form hat:
\[\begin{equation*} \begin{aligned} H_0&: \mu_{12} - \mu_{22} = \mu_{11} - \mu_{21} \\ \Leftrightarrow H_0&: \mu_{12}-\mu_{22}-\mu_{11}+\mu_{21}=0 \end{aligned} \end{equation*}\]
Daraus folgt für den Standardfehler des Interaktionseffekts \(\sigma_{\text{Interaktion}}\):
\[\begin{equation*} \sigma_{\text{Interaktion}} = \sqrt{\frac{\sigma^2}{N/4} + \frac{\sigma^2}{N/4} + \frac{\sigma^2}{N/4} + \frac{\sigma^2}{N/4}} = \frac{4 \sigma}{\sqrt{N}} = 2\sigma_{\text{Haupteffekt}} \end{equation*}\]
D.h. der Standardfehler des Interaktionseffekts \(\sigma_{\text{Interaktion}}\) ist doppelt so groß wie derjenige des Haupteffekts $_{}. Dazu kommt, das überlicherweise die absolute Größe des Interaktionseffekt kleiner ist als diejenige des Haupteffekts. Da dies jedoch nicht den Standardfehler betrifft führt dies zu dazu, dass ein kleinerer Effekt eine höhere Streuung aufweise. D.h. die effektive Effektstärke wird zusätzlich kleiner.
Schauen wir uns diesen Zusammenhang zwischen der Power, der Effektstärke des Haupteffekts und der Effektstärke des Interaktionseffekts etwas systematischer an. In Abbildung 27.9 ist die Power für den Interaktionseffekt in Abhängigkeit vom Verhältnis von Interaktionseffekt zum Haupteffekt abgetragen, wenn die Stichprobengröße für eine Power von \(0.8\) für den Haupteffekt bestimmt wurde.
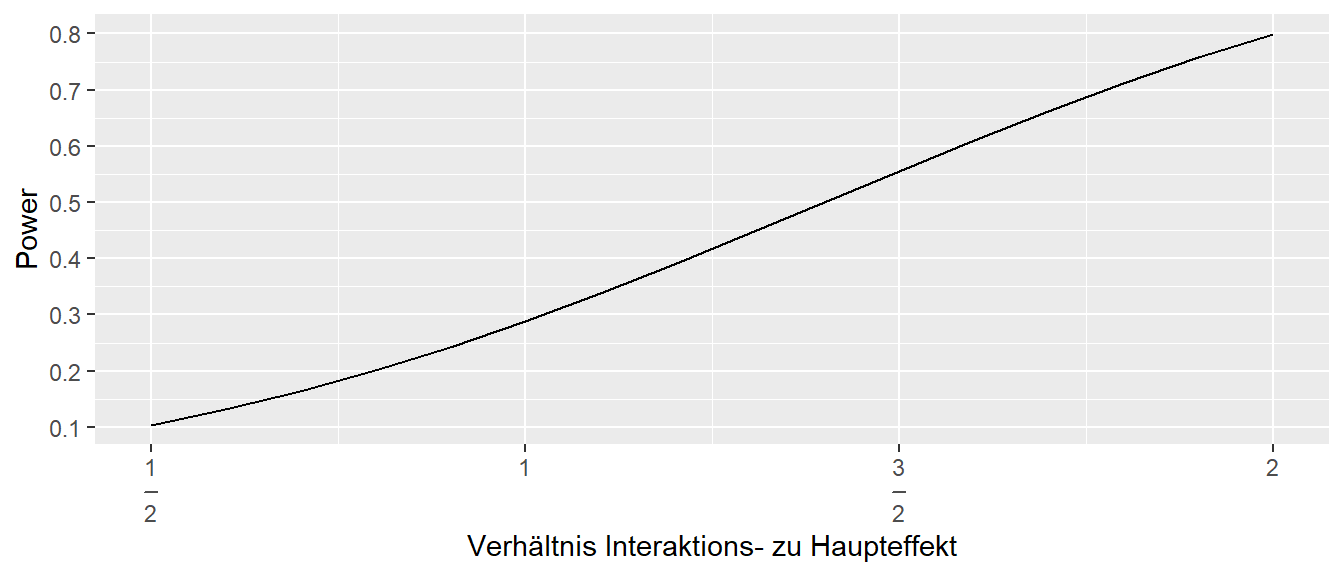
Wir können erkennen, das wenn der Interaktionseffekt nur noch halb so groß ist wie der Haupteffekt, ein nicht unüblicher Zusammenhangt, ist die Power für den Interaktionseffekt nur noch \(0.1\). Erst wenn der Interaktionseffekt die doppelte Größe des Haupteffekts hat, ist dessen Power auch gleich derer für den Haupteffekt. Eine Annahme die praktisch immer unrealistisch ist. Dies führt dazu, dass wenn eine Studie nach der Effektstärke für einen Haupteffekt designed wird aber das eigentliche Interesse einem Interaktionseffekt die Power praktisch immer zu klein ist. Anders herum wird in den Daten ein nicht zu erwartender Interaktionseffekt beobachtet, dann wird dessen Effektstärke oft deutlich überschätzt, da die Power normalerweise zu klein ist und der Effekt extrem sein muss, um tatsächlich statistisch signifikant zu werden. Weitere Probleme in diesem Zusammen sind in der Literatur eingängig beschrieben (Gelman und Stern 2006; Nieuwenhuis, Forstmann, und Wagenmakers 2011) finden aber leider selten ausreichend Beachtung und führen daher zu experimentellen Design die hoffnungslos unterpowert sind (Button u. a. 2013).
27.9 Zum Nach- und Weiterlesen
Dean u. a. (1999) behandelt die Eigenheiten von Interaktionsdesigns sehr umfassend.