| x | y |
|---|---|
| 0 | 3 |
| 1 | 5 |
| 2 | 7 |
| 3 | 9 |
| 4 | 11 |
| 5 | 13 |
13 Einführung
13.1 Back to school
Wir beginnen mit einem uns schon bekannten Konzept, der Punkt-Steigungsform aus der Schule (siehe Formel \(\eqref{eq-slm-psform-1}\)).
\[\begin{equation} y = m x + b \label{eq-slm-psform-1} \end{equation}\]
Wir haben eine abhängige Variable \(y\) und eine lineare Formel \(mx + b\) die den funktionalen Zusammenhang zwischen den Variablen \(y\) und \(x\) beschreibt. Um dies konkret zu machen seien die folgenden Festsetzungen gegeben: \(m = 2\) und \(b = 3\). Die Formel \(\eqref{eq-slm-psform-1}\) wird dann zu:
\[\begin{equation} y = 2 x + 3 \label{eq-slm-psform-2} \end{equation}\]
Um ein paar Werte für \(y\) zu erhalten, setzen wir jetzt verschiedene Werte für \(x\) ein, indem wir \(x\) in Einserschritten zwischen \([0, \ldots, 5]\) erhöhen. Um die Werte darzustellen, verwenden wir zunächst eine Tabelle (vgl. Tabelle 13.1):
Wenig überraschend nimmt \(y\) für den Wert \(x = 0\) den Wert \(3\) an und z. B. für den Wert \(x = 3\) nimmt \(y\) den Wert \(2 \cdot 3 + 3 = 9\) an.
Eine weitere Darstellungsform ist die graphische Darstellung, indem wir die Werte von \(y\) gegen \(x\) in einem Graphen abtragen (siehe Abbildung 13.1).
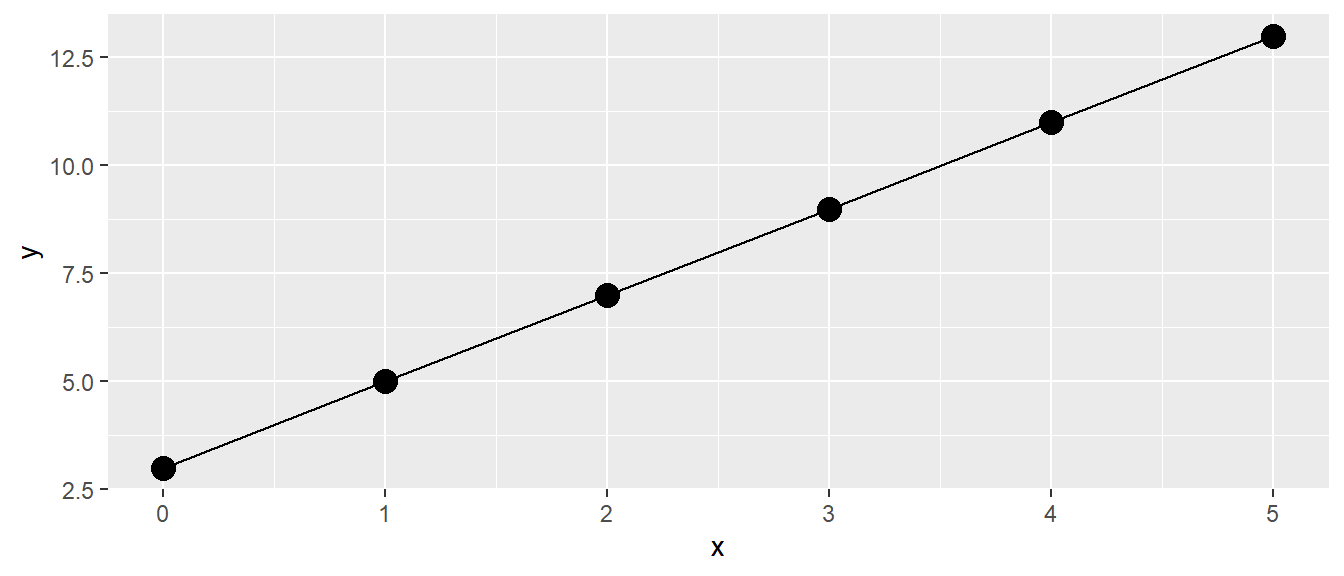
Wiederum wenig überraschend sehen wir einen linearen Zuwachs der \(y\)-Werte mit den größer werdenden \(x\)-Werten. Da in der Definition der Formel \(\eqref{eq-slm-psform-2}\) nirgends festgelegt wurde, dass diese nur für ganzzahlige \(x\)-Werte gilt, haben wir direkt eine Gerade durch die Punkte gelegt. Somit sollte auch die Bedeutung von \(m\) und \(b\) direkt klar sein. Die Variable \(m\) bestimmt die Steigung der Gleichung, während \(b\) den y-Achsenabschnitt beschreibt.
Definition 13.1 (\(y\)-Achsenabschnitt) Der y-Achsenabschnitt ist der Wert, den \(y\) einnimmt, wenn \(x\) den Wert \(0\) annimmt. Sei \(y\) durch eine lineare Gleichung \(y = mx + b\) definiert, dann wird der y-Achsenabschnitt durch den Wert \(b\) bestimmt.
Die Variable \(m\) hingegen bestimmt die Steigung der Geraden.
Definition 13.2 (Steigungskoeffizient) Wenn \(y\) durch eine lineare Gleichung \(y = mx + b\) definiert ist, dann bestimmt die Variable \(m\) die Steigung der dazugehörenden Geraden. D. h., wenn sich die Variable \(x\) um eine Einheit vergrößert (verkleinert), wird der Wert von \(y\) um \(m\) Einheiten größer (kleiner). Gilt \(m < 0\), dann umgekehrt.
Diese beiden trivialen Konzepte mit eigenen Definitionen zu versehen, erscheint im ersten Moment vielleicht etwas übertrieben. Wie sich allerdings später zeigen wird, sind diese beiden Einsichten immer wieder zentral, wenn es um die Interpretation von linearen statistischen Modellen geht.
Soweit so gut. Führen wir direkt ein paar Symbole ein, die uns später noch behilflich sein werden. Sei jetzt die Menge der \(x\)-Werte gegeben \(x = [0, 1, 2, 3, 4, 5]\). Streng genommen handelt es sich wieder um ein Tupel, da wir jetzt die Reihenfolge nicht mehr ändern. Wir führen nun einen Index \(i\) ein, um einzelne Werte in dem Tupel über ihre Position zu bestimmen, und wir hängen diesen Index \(i\) an \(x\) an. Dann wird aus \(x\), \(x_i\).
| Index \(i\) | \(x\)-Wert |
|---|---|
| 1 | 0 |
| 2 | 1 |
| 3 | 2 |
| 4 | 3 |
| 5 | 4 |
| 6 | 5 |
Damit können wir jetzt einen speziellen Wert, zum Beispiel den dritten Wert, mit \(x_3 = 2\) bestimmen. Wenden wir unseren Index auf unsere Formel \(\eqref{eq-slm-psform-1}\) an, folgt daraus, dass \(y\) jetzt auch einen Index \(i\) erhält.
\[ y_i = m x_i + b \qquad i \text{ in } [1,2,3,4,5,6] \]
Wir bezeichnen die beiden Variablen \(m\), die Steigung, und \(b\), den y-Achsenabschnitt, mit neuen Variablen, die ebenfalls einen Index erhalten. Aus \(m\) wird \(\beta_1\) und aus \(b\) wird \(\beta_0\). Damit wird der y-Achsenabschnitt mit \(\beta_0\) bezeichnet und die Steigung wird mit \(\beta_1\) bezeichnet. Dann wird aus unserer Gleichung:
\[\begin{equation} y_i = \beta_0 + \beta_1 x_i \label{eq-slm-psform-beta} \end{equation}\]
Formel \(\eqref{eq-slm-psform-beta}\) ist immer noch die einfache Punkt-Steigungsform. Es wurde lediglich der Index \(i\) eingeführt, um unterschiedliche \(x-y\)-Wertepaare zu identifizieren. Weiterhin wurde der \(y\)-Achsenabschnitt und die Steigung mit neuen Symbolen versehen. Wenn im späteren Verlauf des Skripts die die multiple linearen Regression eingeführt wird, hat diese Nomenklatur große Vorteile, da nicht mehr nur eine einzige \(x\)-Variable vorhanden ist sondern mehrere. Hier vereinfacht die Benutzung von \(\beta\)s die Schreibweise, da zusätzliche \(\beta\)s nach Bedarf angehängt werden können und mit einem fortlaufenden Index (z. B. \(\beta_2, \beta_3, \ldots\)) versehen werden können.
Bezogen auf die Datenpunkte, nochmal jeder Datenpunkt besteht aus zwei Koordinaten, einem \(x\)-Wert und einem \(y\)-Wert. Um die Datenpunkte voneinander auseinander zu halten verwenden wir den Index \(i\) (siehe Abbildung 13.2).
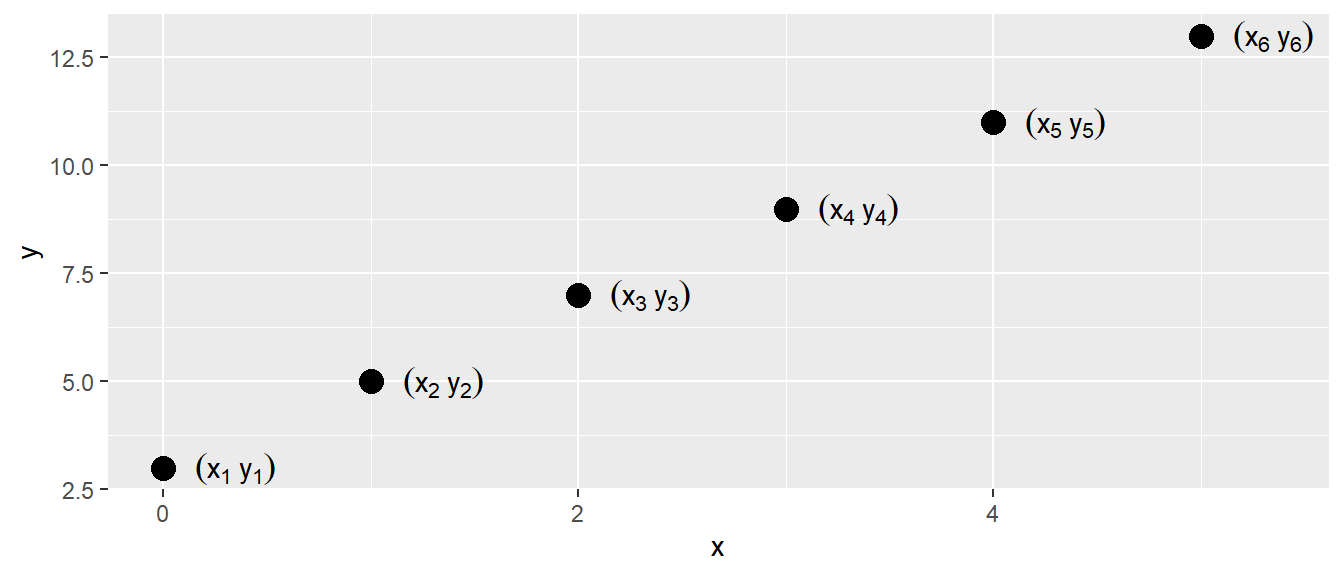
13.2 Funktionaler versus stochastischer Zusammenhang zwischen zwei Variablen
Bei dem bisherigen Zusammenhang handelt es sich um einen funktionalen Zusammenhang zwischen den beiden Variablen \(x\) und \(y\). Funktional deswegen, weil wir ein definiertes mathematisches Modell angeben können, d. h., wir haben eine präzise mathematische Funktion, welche die Beziehung zwischen den beiden Variablen beschreibt. Wenn wir den Wert für \(x\) kennen, dann können wir einen einzigen Wert für \(y\) ausrechnen, indem wir den Wert \(x\) in Formel \(\eqref{eq-slm-psform-1}\) einsetzen. Aus der Schule kennen wir noch die Darstellung \(y = f(x)\). Streng genommen ist diese Darstellung für Formel \(\eqref{eq-slm-psform-1}\) nicht ausreichend, denn um den Wert für \(y\) auszurechnen, benötigen wir auch noch Kenntnis über die Werte \(m\) und \(b\), bzw. in unserer weiteren Darstellung \(\beta_0\) und \(\beta_1\). Daher sollte der Zusammenhang eigentlich mit \(y = f(x, \beta_0, \beta_1)\) bezeichnet werden. Es gilt aber immer noch: Für gegebene \(x, \beta_0\) und \(\beta_1\) ist der Wert für \(y\) fest determiniert.
Wenn wir mit realen Daten arbeiten, funktioniert dieser Ansatz leider nicht direkt. Selbst wenn wir ein Experiment mehrmals genau gleich durchführen, werden wir immer etwas unterschiedliche Werte im Sinne der Messungenauigkeit messen. Wenn wir biologische Systeme messen, kommt hinzu, dass diese in den seltensten Fällen zeitstabil sind, sondern immer bestimmte Veränderungen von einem Zeitpunkt zum nächsten auftauchen.
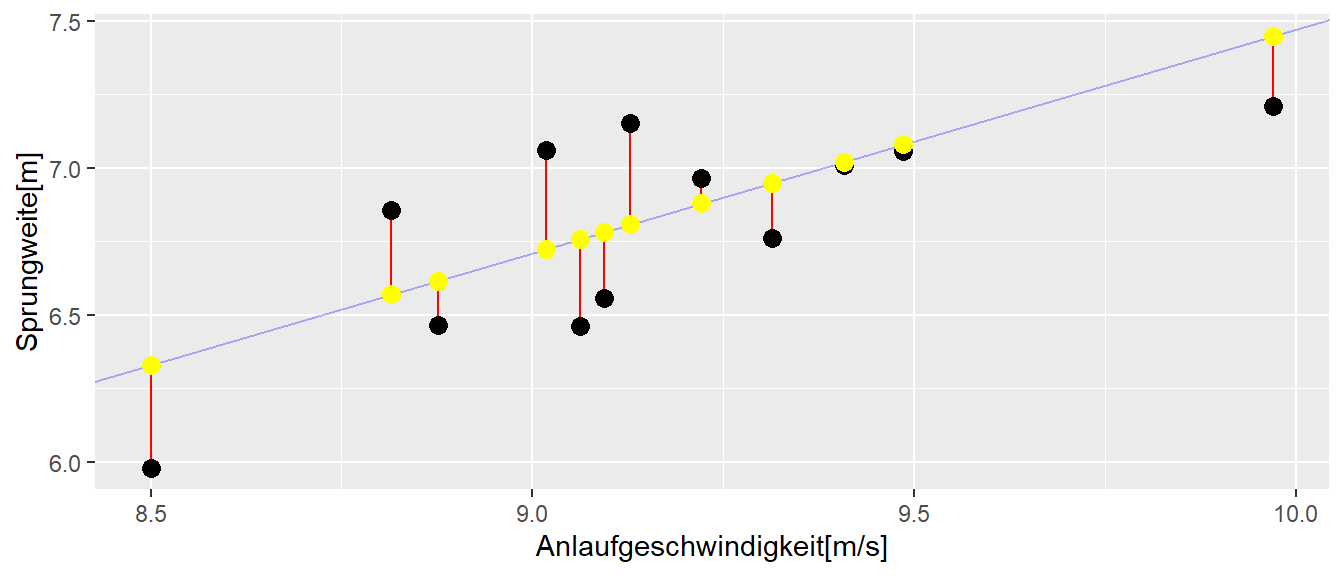
In Abbildung 13.3 ist ein realer Datensatz abgetragen. Auf der \(y\)-Achse sind die Sprungweiten von mehreren Weitspringerinnen gegen die Anlaufgeschwindigkeit auf der \(x\)-Achse abgetragen. Bei der Betrachtung der Daten erscheint ein linearer Zusammenhang zwischen diesen beiden Variablen durchaus plausibel.
In Abbildung 13.3 sind zwei Punkte rot markiert. Die beiden Werte haben praktisch den gleichen \(x\)-Wert, unterscheiden sich allerdings bezüglich ihrer \(y\)-Werte deutlich voneinander. Und dies sind nicht die einzigen Beispielpaare, bei denen die \(x\)-Werte nahe zusammenliegen, während die \(y\)-Werte klar voneinander getrennt sind. Dies steht im Unterschied zu einem funktionalen Zusammenhang nach Formel \(\eqref{eq-slm-psform-1}\). Bei einem rein funktionalen Zusammenhang wird jedem \(x\)-Wert genau ein \(y\)-Wert zugeordnet.
Die Abweichungen kommen durch zufällige Einflussfaktoren wie eben die Veränderungen angesprochener biologischer Faktoren und Messunsicherheiten. Beim Beispiel des Weitsprungs spielen auch noch externe Einflüsse, wie beispielsweise Windverhältnisse, eine Rolle. Vielleicht hatte der Springer beim zweiten Mal auch keine Lust mehr. Wenn die Punkte zwei unterschiedliche Springer darstellen, kommt hinzu, dass zwei Weitspringer bei identischer Anlaufgeschwindigkeit unterschiedliche Sprungfähigkeiten haben oder auch technisch nicht gleich gesprungen sind, und so weiter. Insgesamt führen all diese Einflüsse dazu, dass wir nicht mehr einen streng funktionalen Zusammenhang zwischen unseren beiden Variablen \(x\) (der Anlaufgeschwindigkeit) und \(y\) (der Sprungweite) vorfinden. Es handelt sich um einen stochastischen Zusammenhang zwischen den beiden Variablen. Wie wir mit diesen zufälligen Einflüssen umgehen, ist das zentrale Thema des nächsten Abschnitts und markiert auch unseren Einstieg in die einfache lineare Regression.
13.3 Die einfache lineare Regression
Bleiben wir bei unserem Beispiel aus Abbildung 13.3. Wir versetzen uns in die Lage einer Weitsprungtrainerin, die vor der Aufgabe steht, ihr Training zu optimieren, um die Weitsprungleistung ihrer Athleten zu verbessern. Wir haben uns dazu entschlossen, am Anlauf etwas zu verbessern, wissen jetzt aber nicht, ob das wirklich lohnenswert ist. Von einer befreundeten Trainerin haben wir einen Datensatz mit Anlaufgeschwindigkeiten und den dazugehörigen Sprungweiten erhalten. Schauen wir uns zunächst einmal die Struktur der Daten an.
| jump_m | v_ms |
|---|---|
| 4.36 | 6.13 |
| 4.31 | 6.39 |
| 4.56 | 6.56 |
| 4.75 | 6.44 |
| 5.52 | 7.30 |
| 5.63 | 7.19 |
| 5.70 | 7.30 |
In Tabelle 13.3 sind die ersten \(7\) Zeilen der Sprungdaten abgebildet. Die Daten zeigen eine einfache Struktur mit zwei Spalten. jump_m bezeichnet die Sprungweiten und v_ms die Anlaufgeschwindigkeiten. Damit wir die Datenpaare voneinander unterscheiden bzw. identifizieren können, führen wir unseren bereits besprochenen Index \(i\) ein und können so einzelne Paare ansprechen.
| i | jump_m | v_ms |
|---|---|---|
| 1 | 4.36 | 6.13 |
| 2 | 4.31 | 6.39 |
| 3 | 4.56 | 6.56 |
| 4 | 4.75 | 6.44 |
| 5 | 5.52 | 7.30 |
| 6 | 5.63 | 7.19 |
| 7 | 5.70 | 7.30 |
Daher hat zum Beispiel der dritte Datenpunkt \(i = 3\) die Datenwerte \(\text{jump}_3 = 4.31\) und \(\text{v}_3 = 6.56\).
Das waren bisher aber nur Formalitäten. Wir wollen jetzt den Zusammenhang zwischen den beiden Variablen modellieren. Wir könnten wahrscheinlich auch einfach Pi-mal-Daumen abschätzen, wie groß der Zusammenhang ist. Wenn wir jetzt aber einen unserer Läufer haben, der z.B. etwa \(9m/s\) anläuft, welchen Vergleichswert nehmen wir dann aus Abbildung 13.3? Den unteren oder den oberen der beiden roten Werte? Oder vielleicht den Mittelwert? Welchen Wert nehmen wir, wenn unser Athlet mit \(v=9.7m/s\) anläuft? Da haben wir leider keinen Vergleichswert in unserer Tabelle. Daher wäre es schon ganz praktisch, eine Formel nach dem Muster von Formel \(\eqref{eq-slm-psform-beta}\) zu haben. Wie wir allerdings schon festgestellt haben, geht dies nicht so einfach, da wir eben das Problem mit den Einflussfaktoren haben, die dazu führen, dass die Werte nicht präzise auf einer Geraden liegen. Somit liegt die Herausforderung nun darin, eine Gerade zu finden, die möglichst genau die Daten widerspiegelt.
In Abbildung 13.4 sind die Daten zusammen mit verschiedenen möglichen Geraden abgebildet. Eine kurze Überlegung macht schnell klar, dass es im Prinzip unendlich viele unterschiedliche Geraden gibt, die durch die Datenpunkte gelegt werden können. Da jede Gerade durch die beiden Parameter \(\beta_0\) und \(\beta_1\) spezifiziert ist, gibt es somit auch unendlich viele Kombinationen von \(\beta_0\) und \(\beta_1\), die die jeweiligen Geraden definieren. Um nun eine spezielle Gerade aus den unendlich vielen Geraden auswählen zu können, benötigen wir ein Kriterium, das definiert, was eine besser passende versus eine schlechter passende Gerade durch die gegebenen Punkte ist. Das heißt, wir suchen eine Gerade, die im Sinne eines Kriteriums optimal ist. Tatsächlich gibt es verschiedene Möglichkeiten, Kriterien zu entwickeln. Das am weitesten verbreitete und auch intuitiv nachvollziehbare Kriterium basiert auf den quadrierten Abweichungen der Geraden von den Datenpunkten (engl. least squares). Versuchen wir daher nun, die Herleitung der least squares schrittweise nachzuvollziehen.
13.4 Methode der kleinsten Quadrate
Fangen wir dazu zunächst einmal mit den einfachen Abweichungen an, also nicht den quadrierten Abweichungen. In Abbildung 13.5 ist zur Übersicht nur ein Ausschnitt der Daten zusammen mit einer möglichen Geraden eingezeichnet. Die senkrechten Abweichungen der Geraden zu den jeweiligen Datenpunkten sind rot eingezeichnet. Es ist ersichtlich, dass für diese Wahl der Geraden zwei Punkte ziemlich genau auf der Geraden liegen, während die anderen Punkte oberhalb bzw. unterhalb der Geraden liegen. Ein mögliches Kriterium könnte dementsprechend sein, diejenige Gerade aus den unendlich vielen zu finden, bei der die Abweichungen (die roten Linien) ein Minimum annehmen.
Um die Abweichungen (rote Linien) berechnen zu können, benötigen wir für jeden beobachteten Wert den dazugehörigen Punkt auf der Geraden. Wenn wir die Gerade schon hätten, wäre das kein Problem. Bisher haben wir allerdings nur die Formel der Geraden. Die Punkte auf der Geraden sind mithilfe der Formel genau diejenigen \(y\)-Werte, die für die jeweiligen \(x\)-Werte mittels \(\beta_0 + \beta_1 x_i\) berechnet werden. Die Abweichung für einen Punkt \(y_i\) von der Geraden lässt sich somit wie folgt berechnen:
\[\begin{equation*} \text{Abweichung}_i = y_i - (\beta_0 + \beta_1 x_i) \end{equation*}\]
Entsprechend führt unser Kriterium, die Summation der Abweichungen über alle Punkte, zu folgender Formel:
\[\begin{equation*} \text{min}\sum_{i=1}^n y_i - (\beta_0 + \beta_1 x_i) = \sum_{i=1}^n y_i - \beta_0 - \beta_1 x_i \end{equation*}\]
Wir verschärfen das Kriterium, um eine optimale Gerade zu finden, indem wir größere Abweichungen stärker gewichten wollen als kleinere. Das heißt, große Abweichungen zwischen der Geraden und den Datenpunkten sollen stärker berücksichtigt werden als kleine Abweichungen. Dies können wir erreichen, indem wir die Abweichungen quadrieren. Dementsprechend erhalten wir die folgende Gleichung:
\[\begin{equation} E(\beta_0, \beta_1) = \sum_{i=1}^n(y_i - (\beta_0 + \beta_1 x_i))^2 \label{eq-slm-basics-rms-1} \end{equation}\]
Mit \(E(\beta_0, \beta_1)\) wird ausgedrückt, dass die Summe von der Wahl der beiden Parameter \(\beta_0\) und \(\beta_1\) abhängt. \(E\) ist eine Funktion von \(\beta_0\) und \(\beta_1\). Um unsere Gerade zu bestimmen, suchen wir daher das Minimum der Funktion \(E(\beta_0, \beta_1)\) (\(E\) steht hier für “error”).
Die Abweichungen der Punkte auf der Geraden von den tatsächlichen Datenpunkten spielen in der weiteren Betrachtung immer wieder eine wichtige Rolle und haben daher einen eigenen Term. Die Abweichungen werden als Residuen \(e_i\) bezeichnet. Dementsprechend kann die Minimierungsgleichung auch so dargestellt werden:
\[\begin{equation*} \text{min} \sum_{i=1}^n e_i^2 \end{equation*}\]
Es gilt \(e_i := y_i - (\beta_0 + \beta_1 x_i)\). Insgesamt ergibt sich:
\[\begin{equation*} E(\beta_0, \beta_1) = \sum_{i=1}^n e_i^2 = \sum_{i=1}^n (y_i - \beta_0 - \beta_1 x_i)^2 \end{equation*}\]
Das Minimum lässt sich nun bestimmen, indem wir die partiellen Ableitungen von \(E\) nach \(\beta_0\) und \(\beta_1\) berechnen und, wie wir es aus der Schule kennen, diese gleich Null setzen:
\[\begin{align*} \frac{\partial E(\beta_0, \beta_1)}{\partial \beta_0} &= -2 \sum_{i=1}^n (y_i - \beta_0 - \beta_1 x_i) = 0 \\ \frac{\partial E(\beta_0, \beta_1)}{\partial \beta_1} &= -2 \sum_{i=1}^n x_i (y_i - \beta_0 - \beta_1 x_i) = 0 \end{align*}\]
Diese Gleichungen bilden ein Gleichungssystem mit zwei Unbekannten \(\beta_0\) und \(\beta_1\) und können mit etwas Algebra nach \(\beta_0\) und \(\beta_1\) aufgelöst werden (siehe Kapitel 13.7). Dies führt zu den folgenden Lösungen für \(\beta_0\) und \(\beta_1\):
\[\begin{align} \label{eq-slm-basics-norm-1} \hat{\beta_1} &= \frac{\sum_{i=1}^n (x_i - \bar{x})(y_i - \bar{y})}{\sum_{i=1}^n (x_i - \bar{x})^2} \\ \label{eq-slm-basics-norm-2} \hat{\beta_0} &= \bar{y} - \hat{\beta_1} \bar{x} \end{align}\]
\(\bar{x}\) und \(\bar{y}\) sind die Mittelwerte von \(x_i\) und \(y_i\). Diese beiden Gleichungen werden als die Normalengleichungen bezeichnet.
Wir führen noch einen weiteren Term ein: den vorhergesagten Wert \(\hat{y}_i\) von \(y_i\) anhand der Geradengleichung. Das Hütchen über \(y_i\) zeigt an, dass es sich um einen geschätzten Wert handelt. Wenn wir \(\beta_0\) und \(\beta_1\) anhand der Normalengleichungen bestimmen, dann sind das mit großer Wahrscheinlichkeit nicht die wahren Werte aus der Population, sondern wir haben sie nur anhand der Daten geschätzt. Daher bekommen die berechneten Werte ebenfalls ein Hütchen \(\hat{\beta}_0\) und \(\hat{\beta}_1\). Insgesamt nimmt die lineare Geradengleichung dann folgende Form an:
\[ \hat{y}_i = \hat{\beta}_0 + \hat{\beta}_1 \cdot x_i \]
D.h. die Residuen können auch mittels \(e_i = y_i - \hat{y}_i\) dargestellt werden. Graphisch sind die \(\hat{y}_i\)s die Werte auf der Geraden für die gegebenen \(x_i\)-Werte.
Gehen wir zurück zu unseren Weitsprungdaten. Wenn wir die Datenpunkte in die Normalengleichungen Formeln \(\eqref{eq-slm-basics-norm-1}\) und \(\eqref{eq-slm-basics-norm-2}\) einsetzen, dann erhalten wir für die Koeffizienten die Werte \(\hat{\beta}_0 = -0.14\) und \(\hat{\beta}_1 = 0.76\). Somit folgt für die Geradengleichung:
\[ \hat{y}_i = -0.14 + 0.76 \cdot x_i \]
Wir erhalten die graphische Darstellung der Geradengleichung indem die \(x_i\)-Werte eingesetzt werden und eine Gerade durch die Punkte gezogen wird. Oder auch einfacher für den größten und den kleinsten \(x_i\)-Wert.
Um uns auch zu vergewissern, dass unsere Berechnungen korrekt sind, schauen wir uns noch einmal an, wie sich \(E\) verhält, wenn wir unterschiedliche Kombinationen von Werten für \(\beta_0\) und \(\beta_1\) in die lineare Gleichung einsetzen.
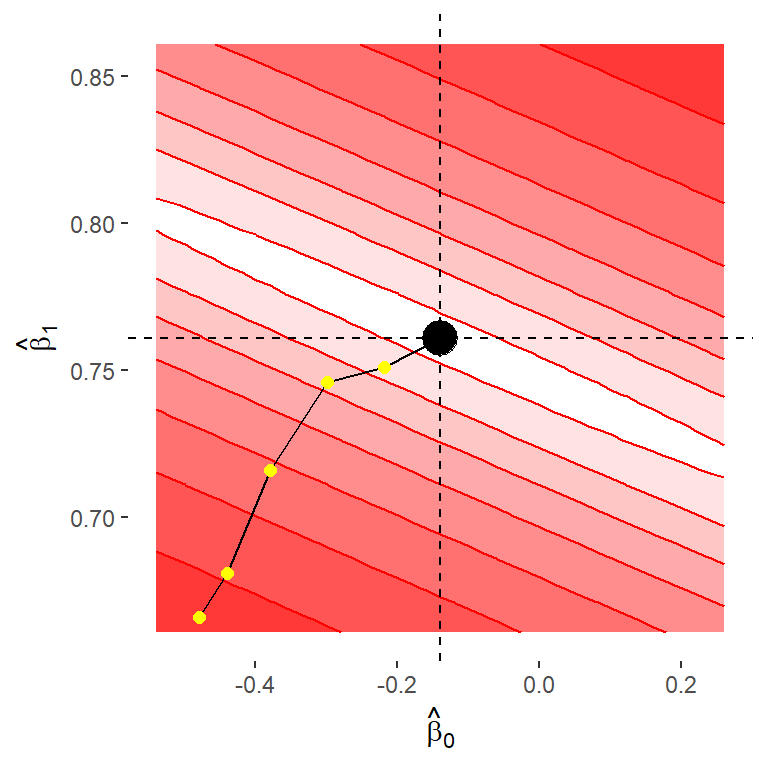
In Abbildung 13.8 sind verschiedene Werte für \(E\) in Form einer Heatmap dargestellt. Die Abweichungen wurden \(log\)-transformiert (d. h., der Logarithmus der \(E\)-Werte wurde berechnet), da sonst die Unterschiede in der diagonalen Bildrichtung zu schnell wachsen und die Unterschiede nicht mehr so einfach zu erkennen sind. Werte näher an Weiß bedeuten kleine Werte, und Werte näher an Rot bedeuten größere Werte von \(E\). Das berechnete Paar für \((\hat{\beta}_0, \hat{\beta}_1)\) mit \(\hat{\beta}_0 = -0.14\) und \(\hat{\beta}_1 = 0.76\) ist schwarz eingezeichnet. Die Abbildung zeigt, dass dieses Wertepaar tatsächlich ein Minimum bezüglich der Funktion \(E\) ist, da in alle Richtungen weg von dem schwarzen Punkt die Werte für \(E\) zunehmen. Da wir nur einen Ausschnitt der möglichen Werte sehen, handelt es sich zunächst um ein lokales Minimum, aber es lässt sich zeigen, dass es sich dabei auch um ein globales Minimum handelt. Diese Eigenschaft hängt mit der Form der Funktion \(E\) zusammen. In Tabelle 13.5 sind beispielhaft ein paar Werte für \(log(E)\) für Paare von \(\beta_0\) und \(\beta_1\) angezeigt, die in Abbildung 13.8 gelb eingezeichnet sind.
| \(\beta_0\) | \(\beta_1\) | \(log(E)\) |
|---|---|---|
| -0.48 | 0.67 | 70.34 |
| -0.44 | 0.68 | 51.85 |
| -0.38 | 0.72 | 22.04 |
| -0.30 | 0.75 | 6.46 |
| -0.22 | 0.75 | 3.77 |
| -0.14 | 0.76 | 2.41 |
Wir können in Tabelle 13.5 erkennen, das das Wertepaar für \(\beta_0\) und \(\beta_1\), welches wir mit Hilfe der Normalengleichung bestimmt haben, denn kleinesten Abweichungswert hat. Also im Sinne unseres Kriteriums ein Optimum darstellt.
Beispiel 13.1 (Nervenleitgeschwindigkeit) In einem klassischen Artikel von Hursh (1939) wurde der Zusammenhang zwischen der Leitungsgeschwindigkeit eines Neurons und dem Durchmesser seines Axons bei erwachsenen Katzen untersucht. Es wurde die maximale Geschwindigkeit der Nervenfasern in verschiedenen Nervenbündeln sowie der Durchmesser der größten Faser in jedem Bündel bestimmt.
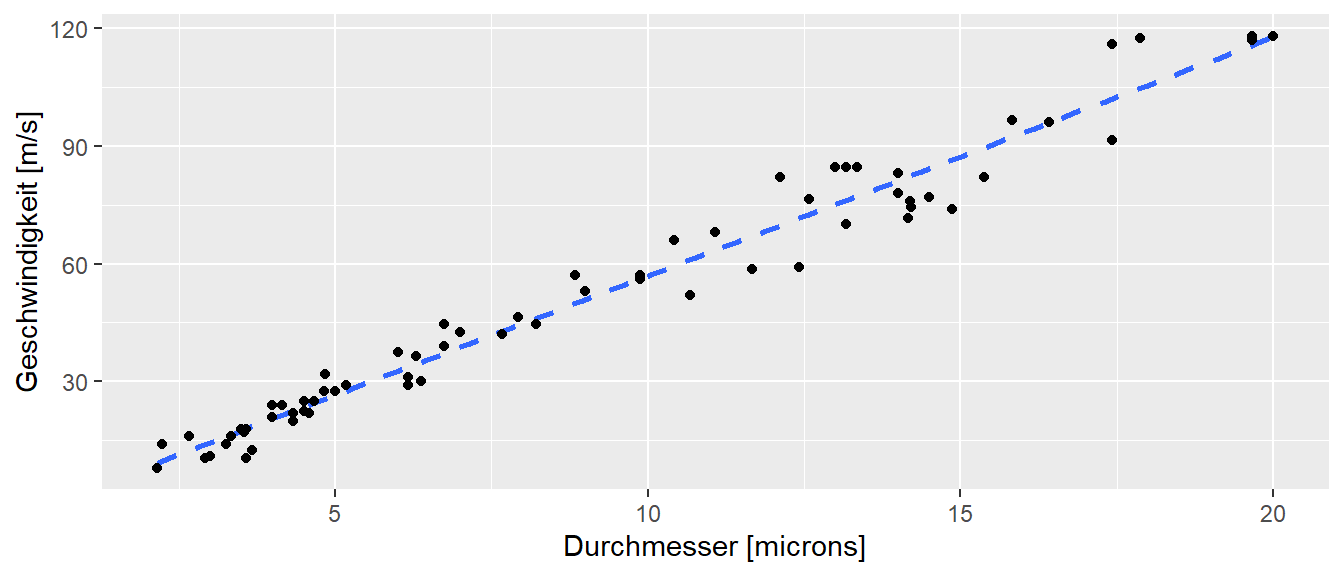
Wie in Abbildung 13.9 zu sehen ist, zeigen die Daten eine nahezu lineare Beziehung zwischen der maximalen Geschwindigkeit und dem Nervendurchmesser. Der \(y\)-Achsenabschnitt liegt bei nahezu null. Dies kann dahingehend interpretiert werden, dass eine Verdoppelung des Faserdurchmessers für den beobachteten Berech der Nervendurchmesser nahezu zu einer verdoppelung der Leitungsgeschwindigkeit führt. Die eingezeichnet Regressionsgerade modelliert die Daten entsprechend gut.
13.5 Was bedeuten die Koeffizienten?
Gehen wir zurück zu unserem Ausgangsproblem der Weitspringer: Was haben wir jetzt durch die Berechnung der Geraden eigentlich gewonnen? Dazu müssen wir erst einmal verstehen, was die beiden Koeffizienten \(\hat{\beta}_0\) und \(\hat{\beta}_1\) bedeuten. Wenn wir zurück zu Formel \(\eqref{eq-slm-psform-1}\) gehen, beschreiben die beiden Koeffizienten den \(y\)-Achsenabschnitt und die Steigung der Geraden. In unserem Beispiel haben wir anhand der Daten einen \(y\)-Achsenabschnitt \(\hat{\beta}_0\) von \(-0.14\) berechnet. Das bedeutet, ein Weitspringer, der mit einer Anlaufgeschwindigkeit von \(x = 0\) anläuft, landet \(14\) cm hinter der Sprunglinie. Dies macht offensichtlich nicht viel Sinn (warum?). Den Grund, warum hier ein offensichtlich unrealistischer Wert berechnet wurde, werden wir später noch genauer betrachten. Trotzdem können wir zwei Eigenschaften von \(\hat{\beta}_0\) beobachten:
- Der Koeffizient hat eine Einheit, nämlich die gleiche Einheit wie die Variable \(y\).
- Ob der Wert sinnvoll interpretierbar ist, hängt von der Verteilung der Daten ab.
Schauen wir uns nun den Steigungskoeffizienten \(\hat{\beta}_1\) an. Der Steigungskoeffizient in Formel \(\eqref{eq-slm-psform-1}\) zeigt an, wie sich der \(y\)-Wert verändert, wenn sich der \(x\)-Wert um eine Einheit verändert. In unserem Fall beschreibt er, welcher Unterschied zwischen zwei Weitspringern zu erwarten ist, die sich in der Anlaufgeschwindigkeit um \(1 \, m/s\) unterscheiden. Das bedeutet, der Steigungskoeffizient ist ebenfalls in der Einheit der \(y\)-Variable zu interpretieren.
Unsere Trainerin kann die berechnete Gerade nun nutzen, um zu überprüfen, ob es sich lohnt, Trainingszeit in den Anlauf zu investieren, und welche Verbesserungen dort zu erwarten sind. Allerdings fehlt dazu noch etwas: Wir wissen nämlich noch nicht, ob die berechnete Gerade auch wirklich die Daten gut widerspiegelt. Im Beispiel erscheint dies anhand der Grafik als relativ plausibel. Das muss aber nicht immer so sein. Wir können für alle möglichen Daten eine Gerade berechnen, ohne dass diese Gerade die Daten auch nur annähernd korrekt wiedergibt. In den Formeln \(\eqref{eq-slm-basics-norm-1}\) und \(\eqref{eq-slm-basics-norm-2}\) steht nirgends, für welche Daten die Berechnung zulässig ist.
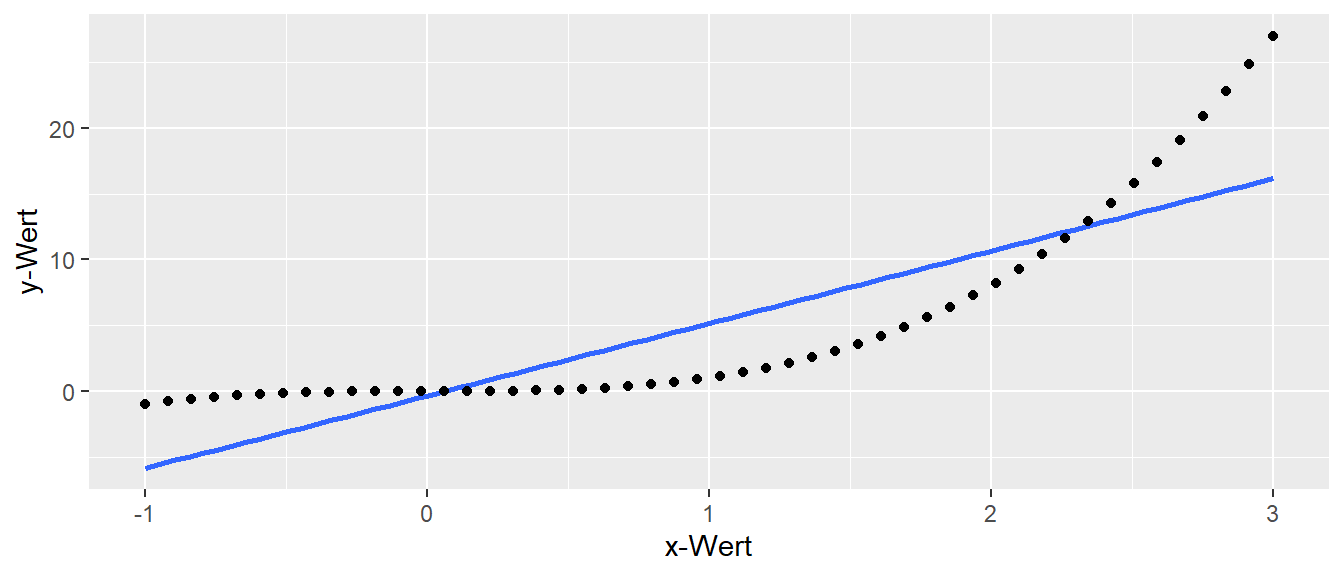
In Abbildung 13.10 sind synthetische Daten der Funktion \(f(x) = x^3\) abgebildet, und die mittels \(\eqref{eq-slm-basics-norm-1}\) berechnete Gerade ist eingezeichnet. Die Gerade ist zwar in der Lage, die ansteigenden Werte zu modellieren, aber nicht die Schwingungen, die durch die kubische Abhängigkeit zustande kommen. Dennoch verhindert nichts die Anwendung der Formel auf diese Daten!
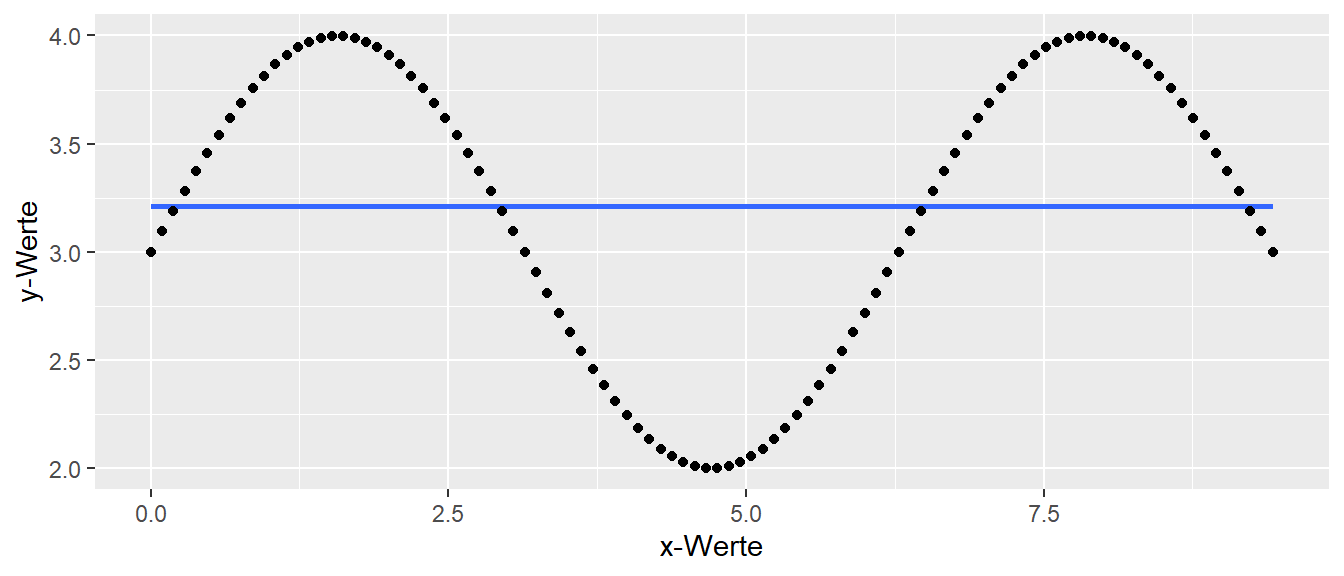
Der gleiche Effekt ist auch in Abbildung 13.11 zu beobachten. Hier besteht eine sinusförmige Abhängigkeit zwischen \(y\) und \(x\). Wir können erneut die Normalengleichungen anwenden und erhalten ein Ergebnis für \(\hat{\beta}_0\) und \(\hat{\beta}_1\). Allerdings repräsentiert die Gerade in keiner Weise den tatsächlichen Zusammenhang zwischen den Daten, wie in Abbildung 13.11 zu sehen ist.
Im nächsten Kapitel werden wir uns daher damit beschäftigen die Repräsentation der Daten näher zu betrachten und zu präzisieren.
Wir nehmen noch eine weitere Eigenschaft der Gerade mit, die zunächst nichts mit der Interpretation der Koeffizienten zu tun hat, aber später noch mal von Interesse sein wird. Die Gerade hat nämlich die Eigenschaft durch den Punkt (\(\bar{x}\), \(\bar{y}\)) zu gehen. Dies kann daran gesehen werden wenn in die Gleichung \(\bar{x}\) für \(x_i\) eingesetzt wird. Anhand der Formel \(\eqref{eq-slm-basics-norm-2}\) der Normalgleichungen kann die Geradengleichung in der folgenden Form dargestellt werden.
\[\begin{equation*} y_i = \hat{\beta}_0 + \hat{\beta}_1 \cdot x_i = \underbrace{\bar{y} - \hat{\beta}_1 \bar{x}}_{\text{Def. }\hat{\beta}_0} + \hat{\beta}_1 \cdot x_i \end{equation*}\]
Wird jetzt für \(x_i\) der Mittelwer der \(x\)-Werte \(\bar{x}\) eingesetzt folgt daraus.
\[ y_i = \bar{y} - \hat{\beta}_1 \bar{x} + \hat{\beta}_1 \bar{x} = \bar{y} \]
D.h. für den Wert \(\bar{x}\) nimmt die Geradengleichung der Wert \(\bar{y}\) an. Für die Sprungdaten ist diese Eigenschaft auch noch mal in Abbildung 13.12 graphisch dargestellt.
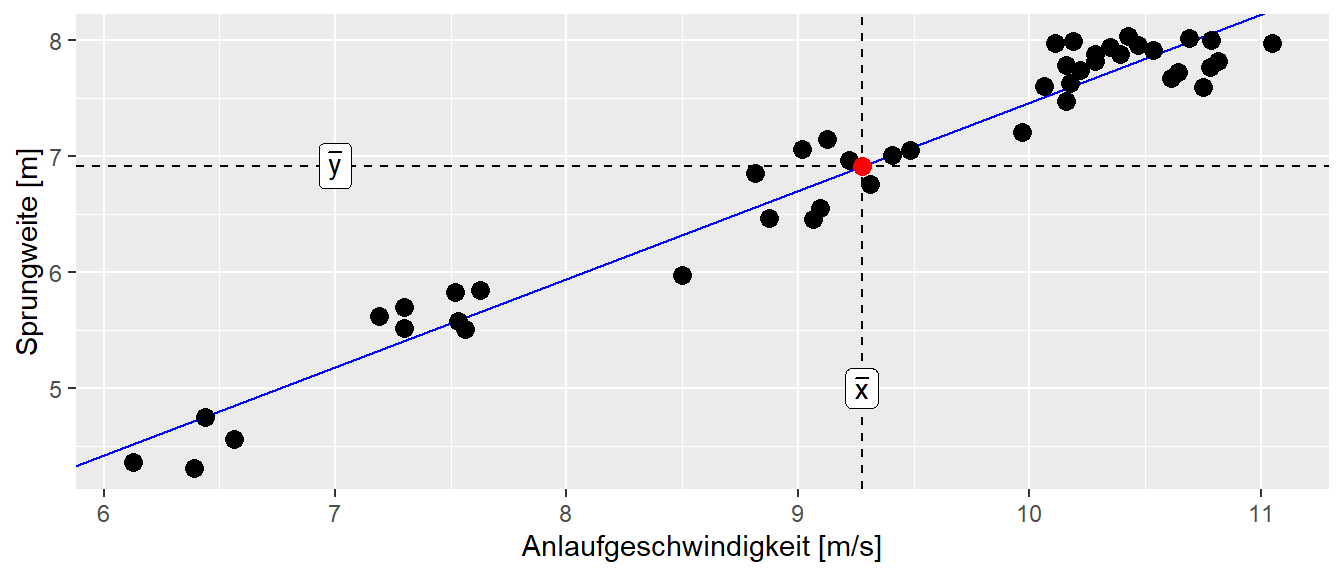
Eine weitere Eigenschaft, die in der weiteren Behandlung der Regression immer wieder auftaucht, bezieht sich auf die \(x\)-Werte. Bei der Regression wird im Allgemeinen davon ausgegangen, dass die beobachteten \(x\)-Werte fixiert sind. Das bedeutet, obwohl die \(x\)-Werte bei einem Experiment möglicherweise zufällige Werte angenommen haben, werden diese in den nachfolgenden Analyseschritten als fixiert bzw. gegeben angesehen.
13.6 Die einfache lineare Regression in R
In R wird eine Regression mit der Funktion lm() berechnet. Die für uns zunächst wichtigsten Parameter von lm() sind der erste Parameter formula und der zweite Parameter data. Mit der Formel wird der Zusammenhang zwischen den Variablen beschrieben, wobei die Namen bzw. Bezeichner aus dem tibble() benutzt werden, das an den zweiten Parameter data übergeben wird. Das bedeutet, die Spaltennamen aus dem tibble() werden in formula verwendet.
In unserem Weitsprungbeispiel konnten wir in Tabelle 13.3 sehen, dass das tibble() zwei Spalten mit den Namen v_ms (den Anlaufgeschwindigkeiten) und jump_m (den Weitsprungweiten) enthielt. Dementsprechend müssen wir diese beiden Bezeichner in formula verwenden, um unser Regressionsmodell zu beschreiben. Die Form der Modellbeschreibung folgt dabei einer bestimmten Syntax, die wir uns zunächst anschauen müssen. Zentrales Element der Syntax ist das Tilde-Zeichen ~ (WIN: ALTGR-+ALTGR-+, MAC: ALT-nALT-n), welches interpretiert wird als modelliert mit. Der Term, der auf der linken Seite steht, bezeichnet die abhängige Variable, während die Terme auf der rechten Seite der Tilde die unabhängigen Variablen spezifizieren. Dementsprechend kann der Satz “Y wird mittels X modelliert” in die Formelsyntax mit Y ~ X übersetzt werden. Die komplette Syntax orientiert sich an einer Arbeit von Wilkinson und Rogers (1973).
Wenn ein konstanter Term in der Syntax benötigt wird, dann wird dieser mit einer \(1\) bezeichnet. Also zum Beispiel, wenn die Formel \(\eqref{eq-slm-psform-beta}\) modelliert werden soll, kann die Syntax y ~ 1 + x verwendet werden. Die beiden Koeffizienten \(\beta_0\) und \(\beta_1\) brauchen nicht explizit angegeben werden, sondern R generiert automatisch die benötigten Koeffizienten. Die Koeffizieten bekommen dann die Namen der Variablen.
Bei der Interpretation der Form kommt noch eine Besonderheit dazu: R geht bei einer Regressionsgleichung standardmäßig davon aus, dass ein \(y\)-Achsenabschnitt mitmodelliert werden soll. Das führt daz, dass der Term +1 automatisch zum Modell hinzugefügt wird. Wenn daher ein Modell ohne einen \(y\)-Achsenabschnitt gefittet werden soll, muss dies R explizit mitgeteilt, indem der Term -1 auf der rechten Seite hinzugefügt. Beispielsweise y ~ x - 1.
Wenn im späteren Verlauf multiple Regressionsmodelle verwendet werden, dann verallgemeinert sich die Syntax einfach indem weitere unabhängige Variablen durch + hinzugefügt werden. Soll beispielsweise der Zusammenhang zwischen einer abhängigen Variablen \(z\) und den beiden unabhängigen Variablen \(x\) und \(y\) modelliert werden, dann würde dies in R mittels y ~ x + y formuliert werden. Variable folgt daraus, dass ein Formel y ~ x_1 + x_2 ausgesprochen übersetzt wird in:
Die abhängige Variable \(y\) wird mittels der unabhängigen Variablen x_1 und x_2 sowie einem konstanten Term modelliert.
In Tabelle 13.6 sind weitere Beispiele für die Syntax von Formeln für lm() gezeigt.
lm() (y-Ab = y-Achsenabschnitt, StKoef = Steigungskoeffizient)
| Modell | Formel | Erklärung |
|---|---|---|
| \(y=\beta_0\) | y ~ 1 |
y-Achsenabschnitt |
| \(y=\beta_0+\beta_1 \times x_1\) | y ~ x |
y-Ab und StKoef |
| \(y=\beta_0+\beta_1 \times x_1+\beta_2 \times x_2\) | y ~ x1 + x2 |
y-Ab und 2 StKoe |
Um unsere Weitsprungdaten mittels lm() zu modellieren, müssen wir den folgenden Befehl verwenden.
lm(jump_m ~ v_ms, data = jump)
Call:
lm(formula = jump_m ~ v_ms, data = jump)
Coefficients:
(Intercept) v_ms
-0.1385 0.7611 Der Rückgabewert von lm() ist in der Standardausgabe nicht besonders hilfreich, da nur die beiden berechneten Koeffizienten ausgegeben werden. Der Term (Intercept) bezeichnet dabei den automatisch hinzugefügten konstanten Term in der Formel, also den \(y\)-Achsenabschnitt \(\hat{\beta}_0\), und v_ms den Steigungskoeffizienten \(\hat{\beta}_1\).
Um aus lm() mehr Informationen herauszubekommen, ist es sinnvoll, das Ergebnis von lm() einer Variablen zuzuweisen. In dieser Arbeit wird dazu in den meisten Fällen eine Variante des Bezeichners mod benutzt, als Kurzform von model. Diese Bezeichnung ist jedoch, wie alle Bezeichner in R, vollkommen willkürlich und entspringt lediglich der Tippfaulheit des Autors.
mod <- lm(jump_m ~ v_ms, data = jump)Um mehr Informationen aus dem gefitteten lm()-Objekt zu erhalten, kann eine der zahlreichen Helferfunktionen verwendet werden. Die wichtigste Funktion ist dabei summary() (?summary.lm).
summary(mod)
Call:
lm(formula = jump_m ~ v_ms, data = jump)
Residuals:
Min 1Q Median 3Q Max
-0.44314 -0.22564 0.02678 0.19638 0.42148
Coefficients:
Estimate Std. Error t value Pr(>|t|)
(Intercept) -0.13854 0.23261 -0.596 0.555
v_ms 0.76110 0.02479 30.702 <2e-16 ***
---
Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
Residual standard error: 0.2369 on 43 degrees of freedom
Multiple R-squared: 0.9564, Adjusted R-squared: 0.9554
F-statistic: 942.6 on 1 and 43 DF, p-value: < 2.2e-16Hier bekommen wir deutlich mehr Informationen. Ganz oben wird zunächst die lm()-Formel angezeigt. Es folgt ein Abschnitt über die Residuen, gefolgt von den Koeffizienten (Coefficients), und im unteren Abschnitt weitere Statistiken. Wir konzentrieren uns zunächst auf die Tabelle im Abschnitt Coefficients. In der ersten Spalte begegnen uns wieder die Bezeichner für die beiden \(\beta\)s in Form von \(\beta_0\) (Intercept) und $_1v_ms`. In der zweiten Spalte daneben stehen die berechneten Koeffizienten, die wir bereits mehrfach gesehen haben. Die weiteren Spalten ignorieren wir zunächst; ihre Bedeutung werden wir in den folgenden Kapiteln erarbeiten.
Bei der Nutzung von lm() werden uns noch weitere Helferfunktionen begegnen, die den Umgang mit dem gefitteten Modell erleichtern. Möchten wir zum Beispiel die beiden Koeffizienten aus dem Modell extrahieren, können wir die Funktion coefficients() oder deren Kurzform coef() verwenden.
coef(mod)(Intercept) v_ms
-0.1385361 0.7611019 Die Funktion coef() gibt einen benannten Vektor zurück, der entweder über die Bezeichner oder über die Position der Koeffizienten angesprochen werden kann. Möchte ich zum Beispiel den Steigungskoeffizienten extrahieren, kann ich die folgende Syntax verwenden:
coef(mod)[1](Intercept)
-0.1385361 oder
coef(mod)['v_ms'] v_ms
0.7611019 Eine etwas übersichtlichere Arbeitsweise besteht darin, das Ergebnis von coef() zunächst einer Variablen zuzuweisen und diese dann weiterzuverwenden.
jump_betas <- coef(mod)
jump_betas[1](Intercept)
-0.1385361 Die Koeffizienten können zum Beispiel verwendet werden, um die Regressionsgerade in ein Streudiagramm einzufügen. Dies kann entweder mit dem ggplot2()-Grafiksystem geschehen:
ggplot(jump,
aes(x = v_ms, y = jump_m)) +
geom_abline(intercept = jump_betas[1],
slope = jump_betas[2],
color = 'red') +
geom_point()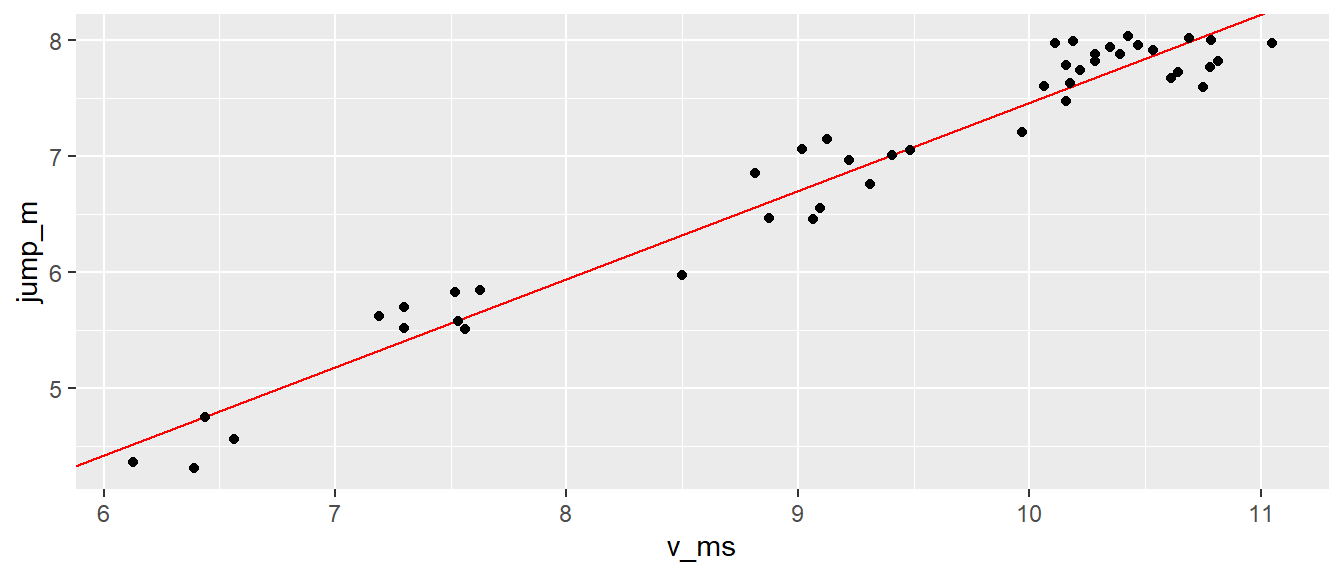
Oder mit dem Standard-Grafiksystem von R. Hier kann der Funktion abline() das gefittete lm()-Objekt direkt übergeben werden, wodurch die Koeffizienten automatisch extrahiert werden.
plot(jump_m ~ v_ms, data = jump)
abline(mod, col = 'red')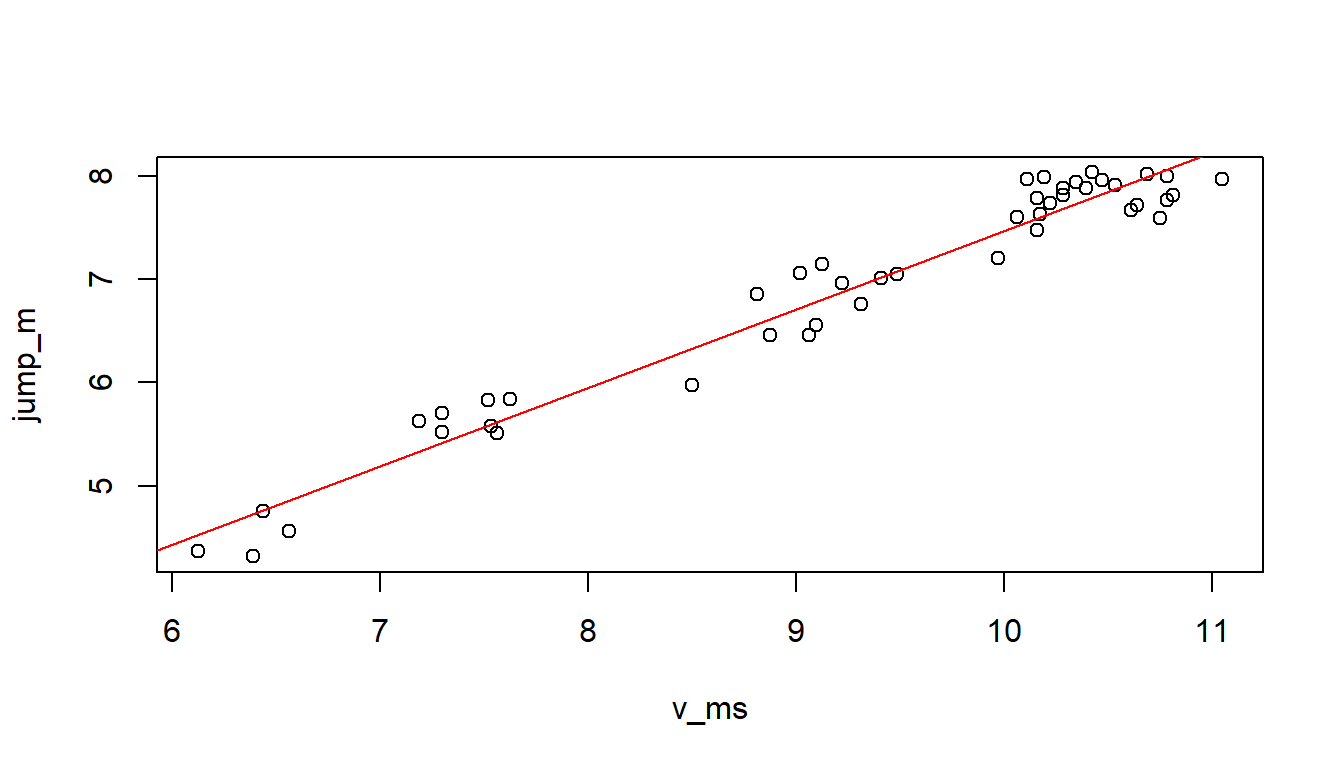
Schauen wir uns nun ein ganz einfaches Beispiel an, bei dem wir tatsächlich wissen, welcher Zusammenhang zwischen den beiden Variablen besteht. Wir halten das Beispiel sehr einfach und nehmen vier verschiedene \(x\)-Werte mit \(x_i = i\). Wir setzen \(\beta_0 = 1\) und \(\beta_1 = 0.5\). Die vier Werte generieren wir mit R, speichern diese in einem tibble() mit dem Bezeichner data, und berechnen die resultierenden Koeffizienten mittels lm().
data <- tibble(
x = 1:4,
y = 1 + 0.5 * x
)
mod <- lm(y ~ x, data)
coef(mod)(Intercept) x
1.0 0.5 Und tatsächlich können wir die korrekten Koeffizienten mittels der einfachen linearen Regression wiedergewinnen. Diesen Ansatz, mithilfe von synthetisch generierten Daten die eingeführten Konzepte und Ansätze zu überprüfen, werden wir im weiteren Verlauf des Skripts immer wieder anwenden. Er bietet die Möglichkeit, relativ einfach und nachvollziehbar das Verhalten verschiedener Ansätze auszutesten.
Zusammenfassend lässt sich sagen, dass wir jetzt gelernt haben, wie wir ein einfaches Regressionsmodell der Form \(\eqref{eq-slm-psform-beta}\) an einen beliebigen Datensatz fitten können. Die Berechnung der beiden Koeffizienten \(\beta_0\) und \(\beta_1\) erfolgt mithilfe der Formeln \(\eqref{eq-slm-basics-norm-1}\) und \(\eqref{eq-slm-basics-norm-2}\). Dabei berechnen wir die Koeffizienten nicht von Hand, sondern lassen sie von R mittels der Funktion lm() durchführen. Die Berechnung ist dabei vollkommen mechanisch, und die Koeffizienten selbst sagen nichts darüber aus, ob das lineare Modell die Daten tatsächlich auch widerspiegelt. Dazu müssen wir noch etwas mehr Theorie aufbauen, um Aussagen darüber treffen zu können, ob das Modell adäquat ist. Dies werden wir in den folgenden Abschnitten und Kapiteln angehen.
13.7 Herleitung der Normalengleichungen (advanced)
Um die Herleitung der Normalengleichungen Schritt-für-Schritt nachvollziehen zu können benötigen wir zunächst einmal ein paar algebraische Tricks.
Für den Mittelwert gilt: \[ \bar{x} = \frac{1}{n}\sum x_i \Leftrightarrow \sum x_i = n \bar{x} \]
Bei Summen und konstanten \(a\) konstant gilt: \[\begin{align} \sum a &= n a \\ \sum a x_i &= a \sum x_i \\ \sum (x_i + y_i) &= \sum x_i + \sum y_i \end{align}\]
Wenn eine Summe abgeleitet wird, kann in die Ableitung in die Summe reingezogen werden. \[ \frac{d}{d x}\sum f(x) = \sum\frac{d}{d x} f(x) \]
Hier ein zwei Umformungen bei Summen und dem Kreuzprodukt bzw. dem Quadrat. \[\begin{alignat}{2} && \sum(x_i-\bar{x})(y_i-\bar{y}) \\ \Leftrightarrow\mkern40mu && \sum (x_iy_i-\bar{x}y_i-x_i\bar{y}+\bar{x}\bar{y}) \nonumber \\ \Leftrightarrow\mkern40mu && \sum x_i y_i - \sum\bar{x}y_i - \sum x_i \bar{y} + \sum \bar{x} \bar{y} \nonumber \\ \Leftrightarrow\mkern40mu&& \sum x_iy_i - n\bar{x}\bar{y}-n\bar{x}\bar{y}+n\bar{x}\bar{y} \nonumber \\ \Leftrightarrow\mkern40mu && \sum x_iy_i - n\bar{x}\bar{y} \nonumber \end{alignat}\] \[\begin{alignat}{2} && \sum(x_i - \bar{x})^2 \\ \Leftrightarrow\mkern40mu && \sum(x_i^2 - 2 x_i \bar{x} + \bar{x}^2) \nonumber \\ \Leftrightarrow\mkern40mu && \sum x_i^2 - 2\bar{x}\sum x_i + \sum\bar{x}^2 \nonumber\\ \Leftrightarrow\mkern40mu && \sum x_i^2 - 2\bar{x}n\bar{x} + n\bar{x}^2 \nonumber \\ \Leftrightarrow\mkern40mu && \sum x_i^2 - n \bar{x}^2 \nonumber \end{alignat}\]Zurück zu unserem Problem. Es gilt \(E\) zu minimieren:
\[\begin{alignat}{2} && E = \sum e_i^2 = \sum (y_i - \hat{y}_i)^2 \\ \Leftrightarrow\mkern40mu && \sum (y_i - (\beta_0 + \beta_1 x_i))^2 \nonumber \\ \Leftrightarrow\mkern40mu && \sum (y_i - \beta_0 - \beta_1 x_i)^2 \nonumber \end{alignat}\]
Die Gleichung hängt von zwei Variablen \(\beta_0\) und \(\beta_1\). Um das Minimum der Gleichung zu erhalten, verfährt man wie in der Schule, indem man die Ableitung gleich Null setzt. Der vorliegenden Fall ist jedoch etwas komplizierter, da die Gleichung von zwei Variablen abhängt. Daher müssen wir die partiellen Ableitungen \(\frac{\partial}{\partial \beta_0}\) und \(\frac{\partial}{\partial \beta_1}\) verwendet. Wir erhalten dadurch ein Gleichungssystem mit zwei Gleichungen (die jeweiligen Ableitungen) in zwei Unbekannten (\(\beta_0\) und \(\beta_1\)). Die Lösung erfolgt, indem zuerst eine Gleichung nach der einen Unbekannten umgestellt wird und das Ergebnis dann in die andere Gleichung eingesetzt wird.
Wir beginnen mit der partiellen Ableitung nach \(\beta_0\) für den y-Achsenabschnitt. (Zurück an die Schule erinnern: Äußere Ableitung mal innere Ableitung)
\[\begin{alignat}{2} && \frac{\partial \sum (y_i - \beta_0 - \beta_1 x_i)^2}{\partial \beta_0} \\ \Leftrightarrow\mkern40mu && \sum\frac{\partial}{\partial \beta_0}(y_i - \beta_0- \beta_1 x_i)^2 \nonumber \\ \Leftrightarrow\mkern40mu && \sum 2(y_i - \beta_0- \beta_1 x_i) (-1) \nonumber \\ \Leftrightarrow\mkern40mu && -2 \sum (y_i - \beta_0- \beta_1 x_i) \nonumber \end{alignat}\] Zum minimieren gleich Null setzen. \[\begin{alignat}{2} && -2 \sum (y_i - \beta_0- \beta_1 x_i) = 0 \nonumber \\ \Leftrightarrow\mkern40mu && \sum (y_i - \beta_0- \beta_1 x_i) = 0 \nonumber \\ \Leftrightarrow\mkern40mu && \sum y_i - \sum \beta_0- \sum \beta_1 x_i = 0 \nonumber \\ \Leftrightarrow\mkern40mu && n \bar{y} - n \beta_0- \beta_1 n \bar{x} = 0 \nonumber \\ \Leftrightarrow\mkern40mu && \bar{y} - \beta_0- \beta_1 \bar{x} = 0 \nonumber \\ \Leftrightarrow\mkern40mu && \bar{y} - \beta_1 \bar{x} = \beta_0\nonumber \\ \Leftrightarrow\mkern40mu && \beta_0= \bar{y} - \beta_1 \bar{x} \end{alignat}\]
Es folgt nach dem gleichen Prinzip die Herleitung für die Steigung \(\beta_1\) und indem die Lösung für \(\beta_0\) eingesetzt wird.
\[\begin{alignat}{2} && \frac{\partial \sum (y_i - \beta_0 - \beta_1x_i)^2}{\partial \beta_1} \\ \Leftrightarrow\mkern40mu && \sum\frac{\partial}{\partial b}(y_i - \beta_0 - \beta_1x_i)^2 \nonumber \\ \Leftrightarrow\mkern40mu && \sum2(y_i - \beta_0 - \beta_1x_i) -x_i \nonumber \\ \Leftrightarrow\mkern40mu && -2 \sum(y_i - \beta_0 - \beta_1x_i)x_i \end{alignat}\] Wiederum gleich Null setzen. \[\begin{alignat}{2} && -2 \sum(y_i - \beta_0 - \beta_1x_i)x_i = 0 \nonumber\\ \Leftrightarrow\mkern40mu && \sum (y_i - \beta_0 - \beta_1x_i)x_i = 0 \nonumber \\ \Leftrightarrow\mkern40mu && \sum (y_i x_i - \beta_0 x_i - \beta_1x_i x_i) = 0 \nonumber \\ \Leftrightarrow\mkern40mu && \sum y_i x_i - \beta_0 \sum x_i - b\sum x_i^2 = 0 \nonumber \\ \Leftrightarrow\mkern40mu && \sum y_i x_i - n \beta_0 \bar{x} - \beta_1\sum x_i^2 = 0 \nonumber \end{alignat}\] Einsetzen der Lösung für \(\beta_0\) führt zu: \[\begin{alignat}{2} \Leftrightarrow\mkern40mu && \sum y_i x_i - n (\bar{y} - \beta_1 \bar{x}) \bar{x} - \beta_1\sum x_i^2 = 0 \nonumber \\ \Leftrightarrow\mkern40mu && \sum y_i x_i - n\bar{y}\bar{x} + n \beta_1\bar{x}^2 - \beta_1\sum x_i^2 = 0 \nonumber \\ \Leftrightarrow\mkern40mu && \sum y_i x_i - n\bar{y}\bar{x} = \beta_1 \sum x_i^2 - \beta_1n \bar{x}^2 \nonumber \\ \Leftrightarrow\mkern40mu && \sum (x_i-\bar{x})(y_i-\bar{y}) = \beta_1 (\sum x_i^2 - n\bar{x}^2) \nonumber \\ \Leftrightarrow\mkern40mu && \frac{\sum (x_i-\bar{x})(y_i-\bar{y})}{\sum x_i^2 - n\bar{x}^2} = \beta_1\nonumber \\ \Leftrightarrow\mkern40mu && \beta_1= \frac{\sum (x_i-\bar{x})(y_i-\bar{y})}{\sum(x_i-\bar{x})^2} \nonumber \end{alignat}\]
Somit erhält man die beiden Normalengleichungen der Regression.
Über diese beiden Gleichungen erhalten wir die gewünschten Koeffizienten \(\hat{\beta_0}\) und \(\hat{\beta_1}\). Die Methode wird als die als die Methode der kleinsten Quadrate bezeichnet oder im Englischen Root-Mean-Square (RMS).