16 Vorhersage
16.1 Vorhergesagte Werte \(\hat{y}_i\)
Wenn ein einfaches lineares Modell gefittet wurde, ist eine zentrale Fragestellung welche Vorhersagen anhand des Modells getroffen werden können. Es wurde schon vorher gezeigt, dass Vorhersagen mittels eines hat Symbols \(\hat{}\) über einer Variable angezeigt wird. Beim einfachen, linearen Regressionmodell liegen die vorhergesagten Werte \(\hat{y}_i\) auf der berechneten Regressionsgerade. Da die Regressionsgerade anhand des Modells berechnet wird, berechnet sich der Werte \(\hat{y}_i\) für einen gegeben \(x\)-Wert nach.
\[ \hat{y} = \hat{\beta_0} + \hat{\beta_0} x \]
Wie schon mehrfach besprochen ist die ermittelte Regressionsgerade inherent unsicher. Die anhand der Daten geschätzten Modellkoeffizienten \(\hat{\beta}_0\) und \(\hat{\beta}_1\) sind ja eben nur Schätzer und wenn die Daten noch einmal erhoben werden würden, dann würden mit großer Wahrscheinlichkeit andere Modellparameter berechnet werden. Diese Unsicherheit drückt sich in den Standardfehlern \(\hat{\sigma}_{\beta_0}\) und \(\hat{\sigma}_{\beta_1}\) aus, die letztendlich auch nur Schätzer der wahren Werte \(\sigma_{\beta_0}\) und \(\sigma_{\beta_1}\) sind. Diese Unsicherheit in den Modellparametern überträgt sich nun aber auch auf die geschätzten Werte \(\hat{y}_i\) und muss bei deren Interpretation der Vorhersagewerte berücksichtigt werden.
16.1.1 Berechnung von \(\hat{y}_i\) in R
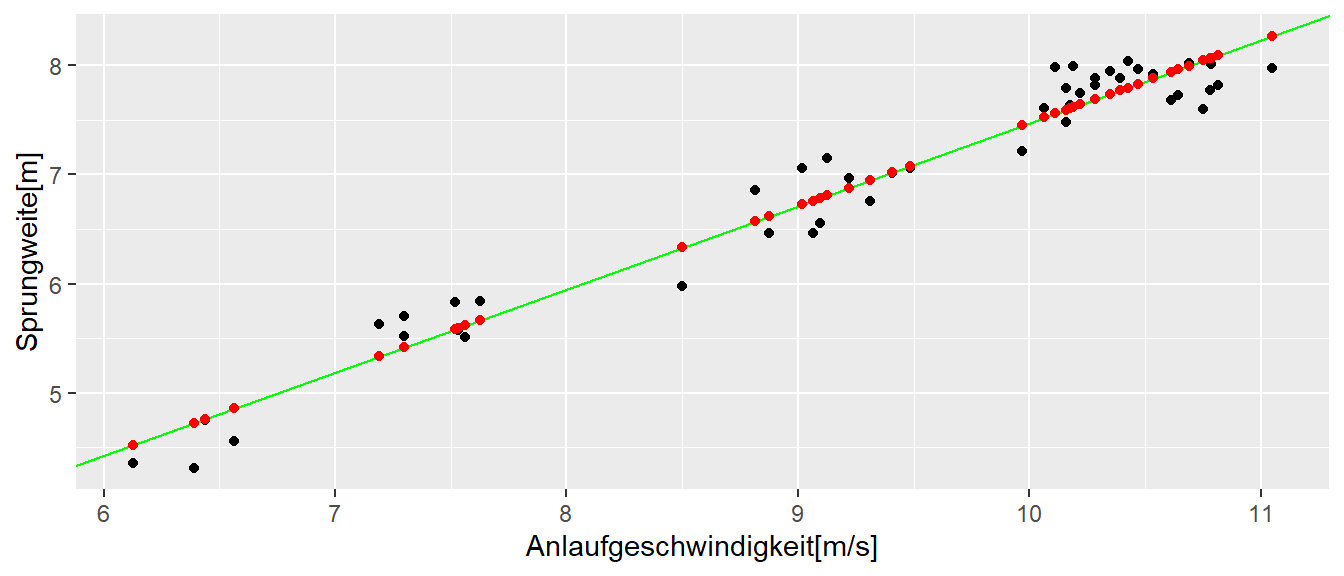
In Abbildung 16.1 sind die bereits behandelten Sprungdaten gegen die Anlaufgeschwindigkeiten zusammen mit der Regressionsgeraden und den vorhergesagten Werten \(\hat{y}_i\) (rot) abgetragen.

In R können die vorhergesagten Werte des mittels lm() gefitteten Modells mit der Hilfsfunktion predict() bestimmt werden. Wenn der Funktion predict() keine weiteren Parameter außer dem lm-Objekt übergeben werden, berechnet predict() die vorhergesagten Werte \(\hat{y}_i\) für alle die \(x\)-Werte die auch zur Anpassung des Modells verwendet wurden. Die Reihenfolge der Werte \(\hat{y}_i\) entspricht dabei den Werten im Original-tibble().
predict(mod)[1:5] 1 2 3 4 5
4.523537 4.725140 4.856256 4.761778 5.416207 Um den Ausdruck übersichtlich zu halten, werden nur die ersten fünf Werte ausgegeben. Als kleine Anwendung, könnten mittels predict() die Residuen auch von Hand ohne die resid()-Funktion berechnet werden.
(jump$jump_m - predict(mod))[1:5] 1 2 3 4 5
-0.16267721 -0.41248842 -0.29359256 -0.01047071 0.09927500 resid(mod)[1:5] 1 2 3 4 5
-0.16267721 -0.41248842 -0.29359256 -0.01047071 0.09927500 Meistens liegt das Interesse jedoch weniger auf den vorhergesagten Werten \(\hat{y}_i\) für die gemessenen Werte, sondern es sollen Werte vorhergesagt werden für neue \(X\)-Werte die nicht im Datensatz enthalten sind. Operational ändert sich nichts, es wird immer noch das gefittete Modell verwendetet und es müssen lediglich die neuen \(X\)-Werte an predict() übergeben werden.
In R kann dies mittels des zweite Parameter in predict() erreicht werden. Soll zum Beispiel die Sprungweite für eine Anlaufgeschwindigkeit von \(v = 11.5[m/s]\) berechnen werden, muss zunächst ein neues tibble() erstellt werden, welches den gewünschten \(x\)-Wert enthält. Dabei muss der Spaltenname in dem neuen tibble() demjenigen im Original-tibble() entsprechen. Ansonsten funktioniert die Anwendung von predict() nicht und es wird ein Fehler geworfen. D.h. zunächst wird eine neues tibble() mit dem gewünschten \(x\)-Wert erstellt.
df <- tibble(v_ms = 11.5)
df# A tibble: 1 × 1
v_ms
<dbl>
1 11.5Wie gesagt, der Name der Spalte mit dem neuen \(x\)-Wert ist der gleiche wie im original Daten-tibble(). Das neue tibble() kann nun zusammen mit dem lm()-Objekt an predict() übergeben werden um den vorhergesagten Wert \(\hat{y}_{\text{neu}}\) zu berechnen.
predict(mod, newdata = df) 1
8.614136 D.h., bei einer Anlaufgeschwindigkeit von \(v = 11.5[m/s]\) ist anhand des Modells eine Sprungweite von \(8.6m\) zu erwarten.
16.2 Unsicherheit in der Vorhersage
Wie schon angesprochen ist das an die Daten angepasste Modell mit Unsicherheiten behaftet. Diese Unsicherheiten drücken sich in den Standardfehler für die beiden Koeffizienten \(\hat{\beta_0}\) und \(\hat{\beta_1}\) aus (siehe Tabelle 16.1).
| Schätzer | \(s_e\) | |
|---|---|---|
| (Intercept) | -0.14 | 0.23 |
| v_ms | 0.76 | 0.02 |
Der vorhergesagte Wert \(\hat{y}\) ist daher für sich alleine ist noch nicht brauchbar, da auch Informationen über dessen Unsicherheit notwendig sind um die Ergebnisse korrekt zu interpretieren. Wenn die Unsicherheit groß ist, dann ist die Interpretation eher schwierig, als wenn die Untersicherheit klein ist. Die Größe der Unsicherheit wird mittels eines Konfidenzintervalls kommuniziert. Wenn das Intervall sehr breit ist, ist die Unsicherheit entsprechend geringer, wenn das Intervall eng ist, ist die mit der Vorhersage verbundene Unsicherheit geringer. Es können hier zwei unterschiedliche Anwendungsfälle voneinander unterschieden werden.
- Der mittlere, erwartete Wert \(\hat{\bar{y}}_{neu}\) (auch \(\hat{E}[y|x]\))
- Die Vorhersage eines einzelnen Wertes \(\bar{y}_{neu}\)
Im konkreten Fall werden damit zwei unterschiedliche Fragestellungen beantwortet. Im 1. Fall lautet die Frage, ich habe eine Trainingsgruppe und möchte wissen was der mittlere Wert der Gruppe anhand des Modells ist, wenn alle eine bestimmte Anlaufgeschwindigkeit \(v_{neu}\) haben. Im 2. Fall lautet die Frage welche Weite eine einzelne Athletin für die Anlaufgeschwindigkeit \(v_{neu}\) springen sollte. In beiden Fällen werden die Athleten nicht genau den Wert des Regressionsmodells treffen. Heuristisch sollte aber einleuchtend sein, dass im 1. Fall der Gruppenvorhersage die auftretenden Streuungen nach oben bzw. nach unten sich gegenseitig im Schnitt ausbalancieren sollten. Im 2. Fall der einzelnen Athletin ist dies nicht der Fall. Daher ist die Vorhersage im 2. Fall mit einer höhere Unsicherheit behaftet als im 1. Fall. Dieser Unterschied sollte sich dementsprechend in den Streuungen bzw. den entsprechenden Varianzen der beiden Vorhersagen wiederspiegeln.
In beiden Fällen ist der vorhergesagte Wert \(\hat{y}_{neu}\) jedoch gleich und entspricht der oben beschriebenen Methode anhand des Modell \(y_{\text{neu}} = \hat{\beta}_0 + \hat{\beta}_1 \cdot x_{\text{neu}}\). D.h. es wird der zu \(x_{\text{neu}}\) entsprechende Wert \(y_{\text{neu}}\) auf der Gerade berechnet.
Die Varianz für den ersten Fall, für den erwarteten Mittelwert errechnet sich nach:
\[ Var(\hat{\bar{y}}_{\text{neu}}) = \hat{\sigma}^2 \left[\frac{1}{n} + \frac{(x_{\text{neu}} - \bar{x})^2}{\sum(x_i - \bar{x})^2}\right] = \hat{\sigma}_{\hat{\bar{y}}_{\text{neu}}}^2 \tag{16.1}\]
Die Wurzel der Varianz ist stellt wie immer den Standardfehler von \(\hat{\bar{y}}_{\text{neu}}\) dar. Das dazugehörige Konfidenzintervall errechnet sich wie immer mittels dem Muster Statistik \(\pm\) Quantile der theoretischen Verteilung multipliziert mit dem Standardfehler mittels:
\[ \hat{\bar{y}}_{\text{neu}} \pm q_{t(1-\alpha/2;n-2)} \cdot \hat{\sigma}_{\hat{\bar{y}}_{\text{neu}}} \]
Die Varianz für die Vorhersage eines einzelnen Wertes errechnet sich dagegen nach:
\[ Var(\hat{y}_{\text{neu}}) = \hat{\sigma}^2 \left[1 + \frac{1}{n} + \frac{(x_{\text{neu}} - \bar{x})^2}{\sum(x_i - \bar{x})^2}\right] = \hat{\sigma}^2 + \hat{\sigma}_{\hat{\bar{y}}_{neu}}^2 = \hat{\sigma}_{\hat{y}_{\text{neu}}}^2 \tag{16.2}\]
Anhand von Gleichung 16.2 ist zu erkennen, dass sich die Varianz für einen einzelnen vorhergesagten Wert \(\hat{y}\) aus zwei Komponenten zusammensetzt. Einmal die Varianz aufgrund des vorhergesagten Mittelwerts und zusätzlich die Residuenvarianz auf Grund des Modells \(\sigma^2\). Insgesamt für das zu dem folgenden Konfidenzintervall:
\[ \hat{y}_{\text{neu}} \pm q_{t(1-\alpha/2;n-2)} \cdot \hat{\sigma}_{\hat{y}_{\text{neu}}} \]
Da \(\sigma^2\) überlicherweise auch nicht bekannt ist, sondern ebenfalls anhand der Daten geschätzt wird, wird der bereits besprochene Schätzer \(\hat{\sigma}^2 = MSE\) verwendet.
In beiden Berechnungen (Gleichung 16.2 und Gleichung 16.1) ist der folgende Term enthalten:
\[ \frac{(x_{\text{neu}} - \bar{x})^2}{\sum(x_i - \bar{x})^2} \]
enthalten. Anhand des Zählers kann abgeleitet werden, dass die Unsicherheit der Vorhersage mit dem Abstand vom Mittelwert der \(x\)-Werte zunimmt. Rein heuristisch macht dies Sinn, da davon ausgegangen werden kann, dass um den Mittelwert der \(x\)-Werte auch die meiste Information über \(y\) vorhanden ist und dementsprechend umso weiter die Werte sich vom \(\bar{x}\) entfernen die Information abnimmt. Im Nenner ist wiederum wie auch beim Standardfehler \(\sigma_{\beta_1}\) des Steigungskoeffizienten \(\beta_1\) zu sehen, dass die Varianz abnimmt mit der Streuung der \(x\)-Werte. Daher, wenn eine Vorhersage in einem bestimmten Bereich von \(x\)-Werten durchgeführt werden soll, dann sollte darauf geachtet werden möglichst diesen Bereich auch zu samplen um die Unsicherheit so klein wie möglich zu halten.
16.2.1 Vorhersagen in R mit predict() (continued)
In R kann die Art des Konfidenzintervalls für die Vorhersage mittels des dritten Arguments zu predict() bestimmt werden. Dabei steht confidence für das Konfidenzintervall der mitteleren Vorhersage und prediction für das Konfidenzintervall eines einzelnen Wertes.
16.2.1.1 Erwarteter Mittelwert
df <- data.frame(v_ms = 11.5) # oder tibble(v_ms = 11.5)
predict(mod, newdata = df, interval = 'confidence') fit lwr upr
1 8.614136 8.482039 8.74623416.2.1.2 Individuelle Werte
predict(mod, newdata = df, interval = 'prediction') fit lwr upr
1 8.614136 8.118445 9.109827Wir erwartet ist das Konfidenzintervall für den individuellen Wert \(\hat{y}\) breiter als das Konfidenzband für den mittleren Wert \(\hat{\bar{y}}\). In diesem konkreten Fall ist der Unterschied allerdings nicht besonder groß.
16.2.2 Konfidenzband für die Regressiongerade
Oftmals ist auch ein Konfidenzband für die gesamte Regressiongerade von Interesse. In diesem Fall kann das Konfidenzband über die folgende Formel nach der Working-Hotelling-Methode abgeschätzt werden. Die Working-Hotelling-Methode ist ein Verfahren, um bei der einfachen linearen Regression ein gleichzeitiges Konfidenzband für die Regressionsgerade zu bestimmen. Im Gegensatz zu einem gewöhnlichen Konfidenzintervall, das nur für einen einzelnen \(X\)-Wert gilt, liefert dieses Band eine Unsicherheitsabschätzung für alle Mittelwertvorhersagen entlang der gesamten Geraden unabhängig davon wie viele Werte tatsächlich benötigt werden. Dies wird dadurch erreicht, dass anstatt einer \(t\)-Quantile ein \(F\)-Quantile verwendet wird.
\[ \bar{Y} \pm W \sigma_{\hat{\bar{Y}}_{new}} \tag{16.3}\]
Mit \(W^2 = 2 F(1-\alpha,2, n-2)\), wobei \(F(1-\alpha,2,n-2)\) die Quartile der \(F\)-Verteilung mit \(df_1 = 2\) bzw. \(df_2 = n-2\) Freiheitsgraden ist.
In Abbildung 16.2 ist das Konfidenzband nach Gleichung 16.3 abgetragen.

Es ist zu erkennen, das das Konfidenzband gegen die jeweiligen Ende der Werte breiter wird. Insbesondere wenn die Vorhersage außerhalb des Bereichs der beobachteten Daten geht, wird die Unsicherheit und damit das Band breiter.
Um das Konfidenzband in R zu bestimmen, muss der \(W\) Wert bestimmt werden. Für das Sprungbeispiel mit \(N = dim(jump)[1]\) und \(\alpha = 0.05\) ergibt sich somit.
N <- 43
alpha <- 0.05
W_sqr <- 2*pf(1-alpha, 2, N - 2)16.3 Die Modellgüte beurteilen
16.3.1 Root-mean-square \(\hat{\sigma}^2\)
Wie wir bereits bei der betrachtung von Vorhersagen gesehen haben, ist die Verbundene Unsicherheit ursächlich in den Formeln Gleichung 16.2 und Gleichung 16.1 von der Residualvarianz \(\sigma^2\) bzw. derem Schätzer \(\hat{\sigma}^2 = MSE\) abhängig. Daher kann dieser Wert, der auch als Standardschätzfehler bezeichnet wird, auch direkt als ein Kriterium der Modellgüte interpretiert werden. Insbesondere die Wurzel aus diesem Wert kann direkt interpretiert werden, da sie die gleichen Einheiten wie die abhängige Variable \(y\) besitzt. Dabei ist weniger die absolute Größe der Residualvarianz von Interesse sondern der Wert ist immer im Verhältnis zur der konkrete Fragestellung, der Streuung der Daten und deren Einheiten.
Im vorliegenden Fall haben wir beispielsweise für das Sprungbeispiel \(\hat{\sigma} = 0.24\) beobachtet. D.h. im Mittel liegen unser Modell knapp einen viertel Meter daneben. Ob eine derart große Abweichung das Modell unbrauchbar bei der Entscheidungsfindung ist, ist keine Entscheidung die über die Statistik getroffen werden kann, sondern diese Entscheidung muss durch die Anwenderin des Modell getroffen werden.
16.3.1.1 Root-mean square \(\hat{\sigma}\) in R
In R wird der Standardschätzfehler \(\hat{\sigma}\) mittels der sigma()-Funktion ausgegeben.
sigma(mod)[1] 0.2369055Letztendlich berechnet diese Funktion nichts anderes als eben die Wurzel aus \(MSE\).
N <- 45
sqrt(sum(resid(mod)**2)/(N-2))[1] 0.2369055Dies ist natürlich der gleiche Wert der auch durch die summary()-Funktion ausgegeben.
summary(mod)
Call:
lm(formula = jump_m ~ v_ms, data = jump)
Residuals:
Min 1Q Median 3Q Max
-0.44314 -0.22564 0.02678 0.19638 0.42148
Coefficients:
Estimate Std. Error t value Pr(>|t|)
(Intercept) -0.13854 0.23261 -0.596 0.555
v_ms 0.76110 0.02479 30.702 <2e-16 ***
---
Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
Residual standard error: 0.2369 on 43 degrees of freedom
Multiple R-squared: 0.9564, Adjusted R-squared: 0.9554
F-statistic: 942.6 on 1 and 43 DF, p-value: < 2.2e-1616.3.2 Der Determinationskoeffizient \(R^2\)
Im Folgenden wird eine weitere Statistik eingeführt, die oft verwendet wird um die Modellgüte zu beurteilen. Sei dazu ein einfaches Modell mit nur vier Datenpunkten betrachtet.
| x | y |
|---|---|
| 0 | 1.26 |
| 1 | 3.29 |
| 2 | 2.52 |
| 3 | 3.04 |
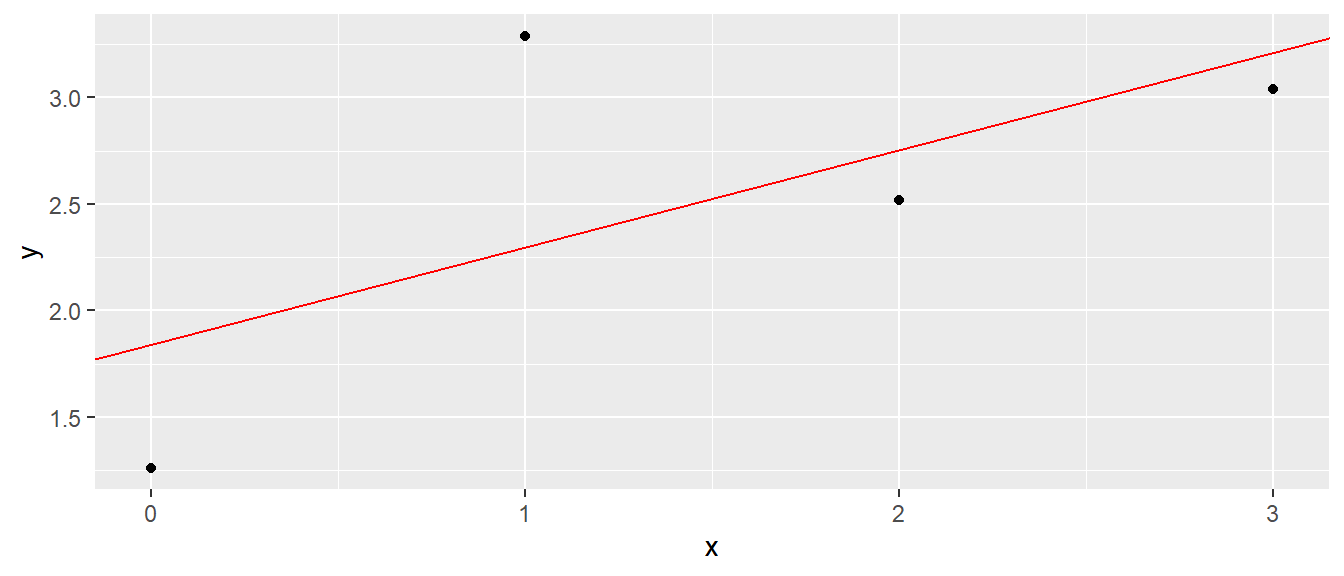
In Abbildung 16.3 ist die Regressionsgerade und die vier Datenpunkte abgebildet.
Schauen wir uns nun noch einmal die möglichen Abweichung bzw. Quadratsummen im einfachen Regressionmodell an. Die Gesamtvarianz beschreibt die quadrierten Abweichungen der \(Y\)-Werte vom Mittelwert \(\mu_Y\) und wird als \(SSTO\) (engl: total sum of squares) bezeichnet. Mit den beobachteten Daten \(y_i\) wird die geschätzte Gesamtvarianz anhand der Summe der quadrierten Abweichungen der \(y_i\)-Werte vom Gesamtmittelwert \(\bar{y}\) berechnet (siehe Gleichung 16.4).
\[ SSTO := \sum_{i=1}^N (y_i - \bar{y})^2 \tag{16.4}\]
Eine weitere Quadratsumme die anhand der Daten berechnet werden kann ist die sogenannte Regressionsvarianz \(SSR\). Diese berechnet sich nach Gleichung 16.5:
\[ SSR :=\sum_{i=1}^N(\hat{y}_i - \bar{y})^2 \tag{16.5}\]
D.h. die Regressionsvarianz \(SSR\) ist die Summe der quadrierte Abweichungen der anhand des Modells vorhergesagten Werte \(\hat{y}_i\)-Werte wiederum vom Gesamtmittelwert \(\bar{y}\). Diese Quadratsumme kann dahingehend interpretieren, dass sie anzeigt, um wie viel die Gesamtstreuung durch das Modell reduziert werden kann. Die dann verbleibende Quadratsumme ist die bereits bekannte Residualvarianz \(SSE\) (siehe Gleichung 16.6).
\[ SSE := \sum_{i=1}^N (y_i - \hat{y}_i)^2 \tag{16.6}\]
D.h. die Quadratsumme der Abweichungen der beobachteten \(Y\)-Werte \(y_i\) von denen anhand des Modells vorhergesagten Werte \(\hat{y}_i\). In Abbildung 16.4 sind die drei verschiedenen Quadratsummen bzw. die zugrundeliegende Abweichungen graphisch dargestellt.
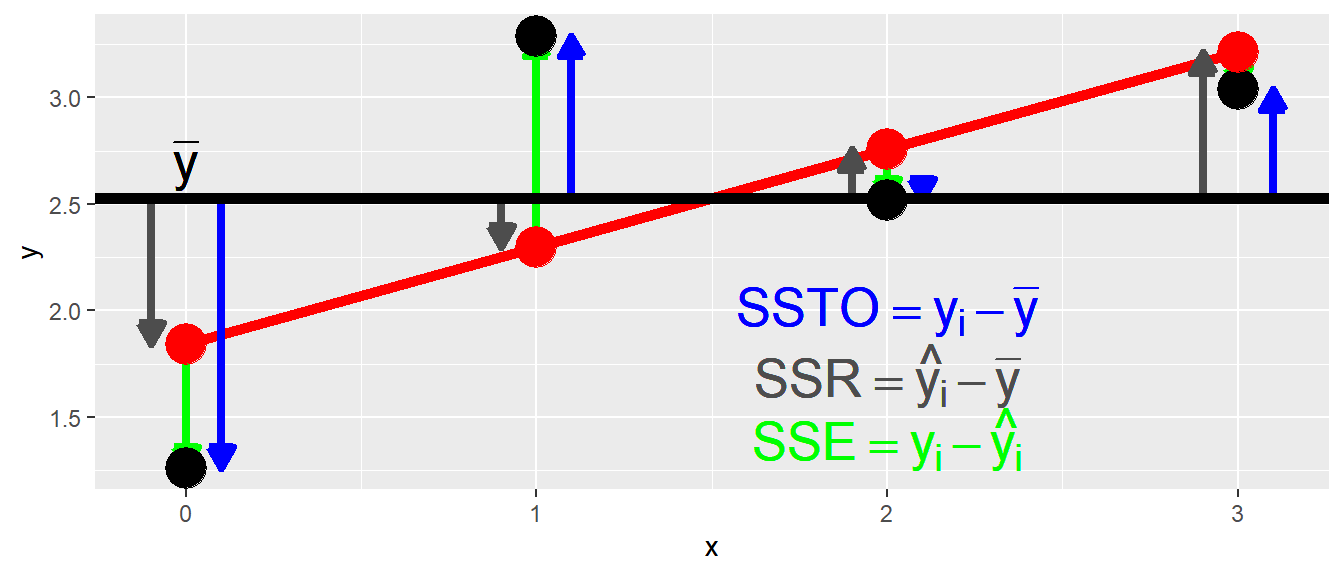
Anhand der Grafik bzw. der Pfeile in Abbildung 16.4 lässt sich erkennen, dass ein additiver Zusammenhang zwischen den Abweichungen besteht. Die blauen Pfeile von \(SSTO\) setzen sich aus der Addition aus den grünen und den grauen Pfeilen zusammen. Bezogen auf \(SSR\) sollte dies verdeutlichen, warum \(SSR\) dahingehend interpretiert werden kann um wie viel Abweichung die Gesamtvarianz \(SSTO\) mittels des Modells vermindert werden kann. Sei dazu zunächst nur der erste Datenpunkt betrachtet. Es soll eine Aussage über den möglichen Wert diese Punktes gegeben werden. Wenn nun kein Modell vorhanden ist, dann ist die beste verfügbare Schätzung für den Wert, der Mittelwert \(\bar{y}\). Der daraus resultierende Fehler wenn der Mittelwert \(\bar{y}\) verwendet wird ist der blaue Pfeil, die Abweichung von \(y_1\) zu \(\bar{y}\). Wenn nun das Modell verwendet wird, dann ist die beste verfügbare Schätzung der zu \(x_1\) gehörende Punkt auf der Geraden. Der anhand des Modell vorhergesagte Wert \(\hat{y}_1\) auf der Gerade ist deutlich näher an den beobachteten Wert \(y_1\) herangerückt ist. Nämlich um den Betrag des grauen Pfeils \(SSR\). Der verbleibender Fehler ist jetzt deutlich kleiner, nämlich der grüne Pfeil \(SSE\). Wenn diese Idee formalisiert wird:
\[ y_i - \bar{y} = y_i - \hat{y}_i + \hat{y}_i - \bar{y} = \underbrace{(y_i - \hat{y}_i)}_{SSE} + \underbrace{(\hat{y}_i - \bar{y})}_{SSR} \]
Um nun die Quadratsummen zu erhalten, wird diese Gleichung quadriert und über alle \(i=1,2,\ldots,N\) aufsummiert. Es lässt sich zeigen, dass die Kreuzprodukte der beiden Komponenten sich gegenseitig auslöschen. Daraus folgt der Zusammenhang:
\[ SSTO = SSR + SSE \]
D.h. auch die Summe der quadrierten Abweichungen, die Gesamtvarianz \(SSTO\) setzt sich aus zwei getrennten Komponenten zusammen. Einmal der Teil der Varianz der anhand des Modells erklärt werden kann (\(SSR\)) und derjenige Teil der nicht anhand des Modells erklärt werden kann (\(SSE\)). Aus diesem Zusammenhang lässt sich eine Metrik erstellen indem das Verhältnis von \(SSR\) to \(SSTO\) gebildet wird.
Dazu sei zunächst untersucht, was passiert wenn ein perfekter Zusammenhang zwischen \(X\) und \(Y\) vorliegt. In Abbildung 16.5 ist ein solcher Zusammenhang abgebildet.
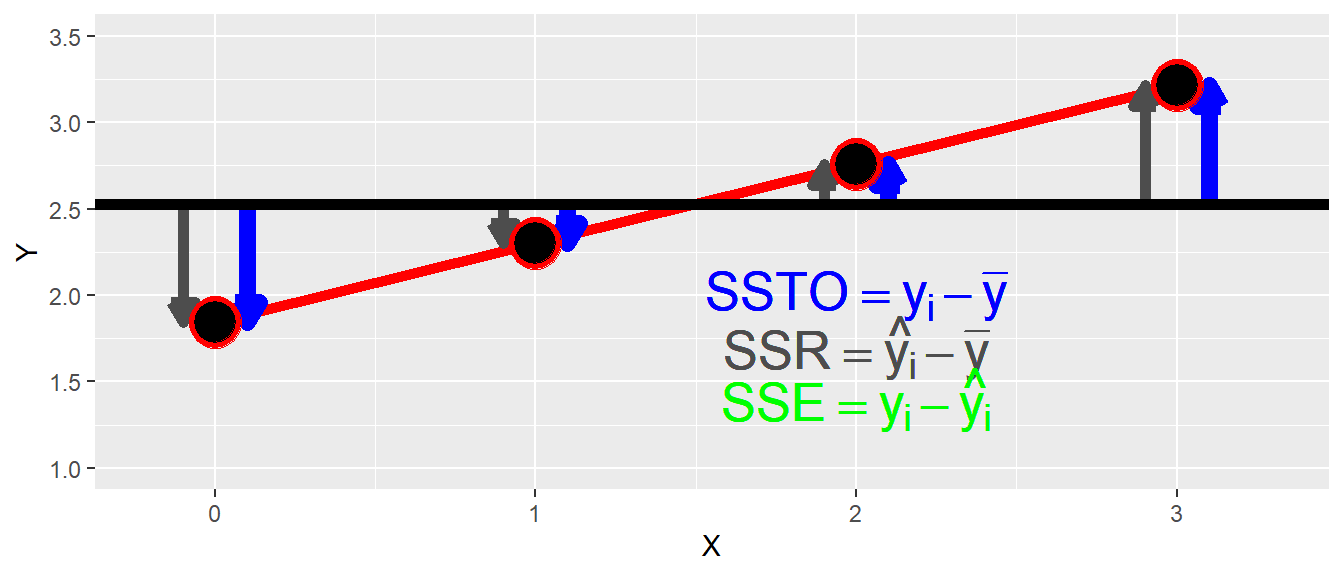
In diesem Fall, liegen die beobachteten Werte \(y_i\) genau auf der Regressionsgeraden. D.h. die Abweichungen \(y_i - \hat{y}_i = 0\) und damit \(SSE = 0\). In diesem Fall folgt für das Verhältnis von \(SSR\) zu \(SSTO\):
\[ \frac{SSR}{SSTO} = 1 \]
In Abbildung 16.6 ist nun der gegenteilige Zusammenhang abgebildet. Es besteht kein Zusammenhang zwischen \(X\) und \(Y\)e. D.h. das Modell liefert keine Informationen zu \(Y\), da die \(Y\)-Werte unabhängig von den \(X\)-Werten sind.
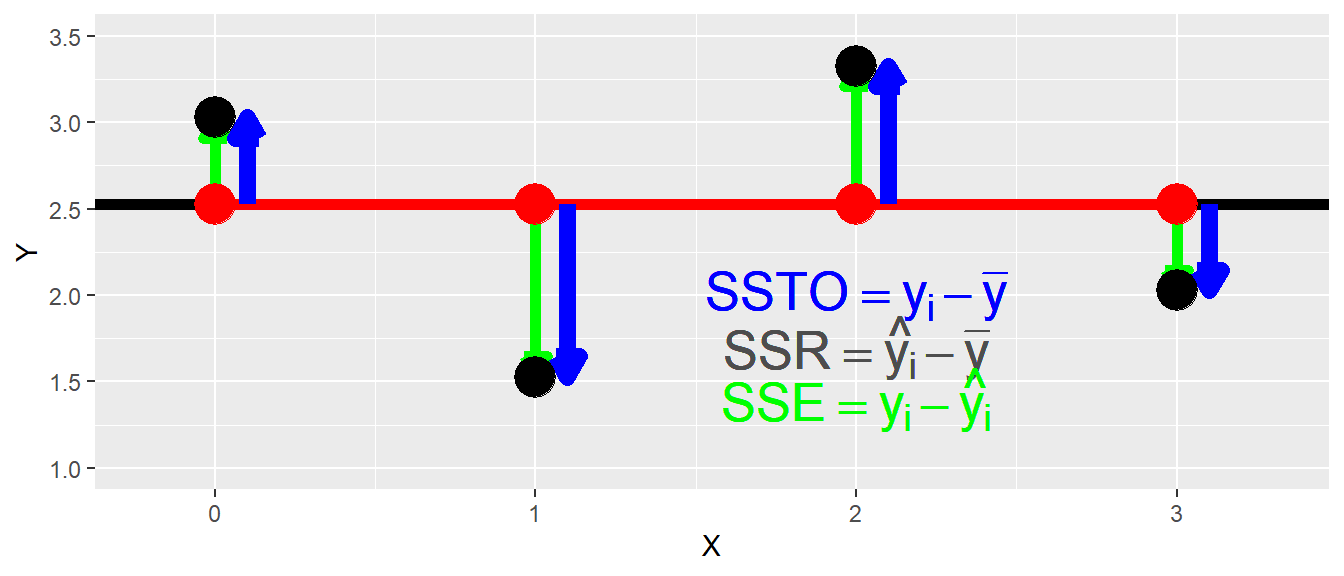
In diesem Fall sollte die Regressionsgerade die Steigung \(\beta_1 = 0\) haben. Der \(y\)-Achsenabschnitt \(\beta_0\) ist in diesem Fall gleich dem Mittelwert \(\bar{y}\) der \(y_i\)-Werte. Für die Abweichungen resultiert daraus, dass nun keine Abweichung zwischen den vorhergesagten Werten \(\hat{y}_i\) und dem Mittelwert \(\bar{y}\) besteht. Es gilt somit \(\hat{y}_i - \bar{y} = 0\). Daraus folgt, dass \(SSR = 0\) gilt. Wird nun wieder das Verhältnis von \(SSR\) zu \(SSTO\) gebildet, dann folgt dementsprechend:
\[ \frac{SSR}{SSTO} = 0 \]
Zusammen zeigen diese beiden Beispiele, das mittels des Verhältnisses von \(SSR\) zu \(SSTO\) eine Metrik entsteht, die wiedergibt wie gut die \(X\) und \(Y\)-Variablen in einenm linearen Zusammenhang stehen. Das Verhältnis wird als Determinationskoeffizient \(R^2\) bezeichnet. Die Metrik ist beschränkt auf Werte zwischen \(0\) und \(1\). Bei einem Wert von \(R^2 = 0\) besteht kein Zusammenhang, während bei \(R^2 = 1\) ein perfekter Zusammenhang besteht. Insgesamt gilt:
\[ R^2 = \frac{SSR}{SSTO} = 1 - \frac{SSE}{SSTO} \in [0,1] \tag{16.7}\]
Es besteht auch ein enger Zusammenhang zwischen dem Determinationskoeffizienten \(R^2\) und dem Korrelationskoeffizienten \(r_{xy} = \pm\sqrt{R^2}\). Dieser Zusammenhang gilt allerdings nur für die einfache lineare Regression und gilt nicht mehr bei der multiplen Regression die wir später kennenlernen werden.
Im Zusammenhang mit dem Determinationskoeffizienten \(R^2\) gilt es auf ein Missverständnis hinzuweisen. Ein hoher \(R^2\) zeigt unglücklicherweise nicht an, dass präzise Vorhersagen mittels des Modells getroffen werden. Der Determinationskoeffzient bestimmt nur die relative Reduktion der Varianz an nicht die Absolute. Ob ein Modell nützlich zur Prädiktion ist, hängt wie oben besprochen sehr eng mit dem absoluten Höhe der Residualvarianz zusammen.
Trotzdem der Determinationskoeffizient \(R^2\) oft verwendet wird sollte nicht verschwiegen werden, dass \(R^2\) zur Beurteilung der Modellgüte nicht sonderlich gut geeignet ist. Die folgenden Ausführung beruhen weitestgehend auf Shalizi (2015). Es lässt sich zeigen, dass \(R^2\) der auch folgendermaßen hergeleitet werden kann:
\[\begin{equation} R^2 = \frac{\beta_1^2Var(X)}{\beta_1^2Var(X)+\sigma^2} \end{equation}\]
Daraus folgt, das wenn die Varianz von \(X\) vergrößert wird \(R^2\) beliebig nahe an \(1\) gebracht werden kann. Genauso, indem die Varianz von \(X\) verkleinert wird, kann \(R^2\) beliebig nahe an \(0\) gebracht werden. Weiterhin ist \(R^2\) auch nicht wirklich hilfreich um die Vorhersagegüte des Modells zu beurteilen, da wenn die Residualvarianz \(\sigma^2\) konstant gehalten wird, nur durch Veränderung der Varianz \(X\) \(R^2\) vergrößert wie auch verkleinert werden kann. Da wie schon erwähnt ein direkter Zusammenhang zwischen dem Korrelationskoeffizienten \(\rho_{XY}\) und \(R^2\) besteht, ist auch die oft verwendete Interpretation von \(R^2\) als der Anteil der durch \(X\) aufgeklärten Varianz von \(Y\) irreführend, da die Korrelation symmetrisch in beiden Variablen ist. Durch die Abhängigkeit von der Varianz von \(X\) kann \(R^2\) auch nicht direkt über Datensätze hinweg verglichen werden, da sich üblicherweise \(Var(X)\) zwischen Datensätzen unterscheiden wird (Shalizi 2015). Für eine umfangreiche Diskussion zu den Problem sei auch die Diskussion auf Gelman (2024) empfohlen.
Im Zusammenhang mit der multiplen Regression gibt es auch noch einen korrigierten Determinationskoeffizient \(R_a^2\). Dieser Determinationskoeffizient hat einen zusätzlichen penalty term der Anahnd der Anzahl der Prädiktoren \(X_i\) berechnet wird. Wie später im Zusammenhang mit der multiplen Regression gezeigt wird, kann der Determinationskoeffizient verbessert werden, indem einfach zusätzlich Variablen in das Modell eingefügt werden. Die Varialben müssen dazu noch nicht einmal einen Zusammenhang mit der abhängigen Variablen \(Y\) haben. Um diese Eigenschaft mit einzubeziehen wird die Anzahl der Variablen penalisiert.
\[ R_a^2 = 1 - \frac{\frac{SSE}{n-p}}{\frac{SSTO}{n-1}} = 1 - \frac{n-1}{n-p}\frac{SSE}{SSTO} \tag{16.8}\]
Damit sind nun mittlerweile auch fast alle Ausgabeinformationen der summary()-Funktion erarbeitet worden. Es fehlt noch die letzte Zeile die im Zusammenhang mit der multiplen linearen Regression betrachtet wird. Insgesamt sollte der Determinationskoeffizient \(R^2\) eher seltener eingesetzt werden und insbesondere wenn es um Modellgüte eigentlich auf Grund der Limitationen eher nicht (siehe auch Schemper (2003)).
16.3.2.1 Determinationskoeffizient \(R^2\) in R
In R wird der Determinationskoeffizienten im Bericht der summary()-Funktion mit angegeben. In Weitsprungbeispiel wird beispielsweise der folgende Wert erhalten:
summary(mod)
Call:
lm(formula = jump_m ~ v_ms, data = jump)
Residuals:
Min 1Q Median 3Q Max
-0.44314 -0.22564 0.02678 0.19638 0.42148
Coefficients:
Estimate Std. Error t value Pr(>|t|)
(Intercept) -0.13854 0.23261 -0.596 0.555
v_ms 0.76110 0.02479 30.702 <2e-16 ***
---
Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
Residual standard error: 0.2369 on 43 degrees of freedom
Multiple R-squared: 0.9564, Adjusted R-squared: 0.9554
F-statistic: 942.6 on 1 and 43 DF, p-value: < 2.2e-16D.h. es wurde ein hoher Determinationskoeffizient bezüglich des linearen Zusammenhang zwischen der Anlaufgeschwindigkeit und der Sprungweite mit \(R^2 = 0.96\) beobachtet. Das Beispiel zeigt aber auch direkt die Limitation des Determinationskoeffizienten \(R^2\). Trotzdem ein hohes \(R^2\) beobachtet wurde, ist dass Modell nur sehr eingeschränkt hilfreich, da der Residualfehler mit \(\hat{\sigma} = 0.24[m]\) relativ hoch ist.
Der \(R^2\) kann natürlich auch relativ einfach von Hand berechnet werden.
ssr <- sum( (predict(mod) - mean(jump$jump_m))**2 )
sst <- sum( (jump$jump_m - mean(jump$jump_m))**2 )
ssr/sst[1] 0.956372416.4 Zum Weiterlesen
In Kapitel 2 Abschnitt 2.5 in Kutner u. a. (2005) lässt sich gut als ergänzendes Material lesen, inklusvie weiterführender Informationen zur Working-Hotelling-Methode (S.52ff).