
8 Eine kleine Welt der Unsicherheit
In den einleitenden Problem aus dem vorhergehenden Abschnitt mit einem Vergleich zwischen zwei Gruppen ist warum überhaupt die Berechnung einer Statistik notwendig ist. Bei der Beantwortung der Frage sind wahrscheinlich Begründungen gefallen wie: “Weil das Ergebnis zufällig sein könnte” oder “Weil wir wissen wollen ob der Unterschied auch signifikant ist” und ähnliche. Diese Antworten sind im Grunde genommen alle korrekt aber es sind zunächst ein paar Konzepte einzuführen um das Problem tatsächlich strukturiert angehen zu können. Diese Konzepte werden in dem folgenden Kapitel entwickelt.
Zunächst wird einem übersichtlichen Konstrukt einer hypothetischen Welt gestartet um das notwendige statistische Modell so einfach wie möglich zu halten. Die Welt, über die eine Aussage getroffen werden soll, besteht aus nur insgesamt \(20\) Personen. In Abbildung 8.1 sind die Bewohner dieser Welt einzeln zu dargestellt. Um nicht \(20\) Namen zu verwenden, sind die Bewohner durchnummeriert von \(1\) bis \(20\) mit einem Prefix \(P\).

Der Gesamtheit aller Personen, oder auch allgemeiner Objekte, über die eine Aussage getroffen werden soll wird jetzt ein Name gegeben. Diese Menge soll als Population bezeichnet werden.
Definition 8.1 (Population) Die Gesamtheit aller Objekte/Dinge/Personen, über die eine Aussage getroffen werden soll, wird als Population oder Grundgesamtheit bezeichnet.
Jeder statistischen Aussage liegt zunächst eine Menge von Objekten/Personen zugrunde über die eine Aussage getroffen werden soll. Im vorliegenden Fall ist die Population sehr übersichtlich, während sie in den meisten Fällen deutlich größer ist. Zum Beispiel alle Personen zwischen \(15-64\) Jahren (ungefähr \(5\) Milliarden Personen) oder alle aktiven Tischtennisspieler in Deutschland (ungefähr \(500.000\)) oder Sportstudierende in Deutschland (über 30.000) oder an Krebs neuerkrankte Personen in der EU (etwa \(3\) Millionen). Die Population hängt damit immer mit der konkreten wissenschaftlichen Fragestellung zusammen die untersucht werden soll.
8.1 Ein Experiment
Basierend auf einer theoretischen Überlegung ist zum Beispiel ein neuer Krafttrainingsansatz entwickelt worden. Nun soll mittels eines Experiments überprüft werden, ob der neue Ansatz dazu führt, dass sich die Beinkraft stärker erhöht als bei einem traditionellen Training. Unglücklicherweise stehen selbst bei der kleinen Welt nur sehr wenige Ressourcen zur Verfügung und es können daher nur sechs Messungen durchführt werden. Aus einem kürzlich durchgeführten Zensus sind jedoch die Beinkraftwerte der gesamten Population bekannt. Sei daher zunächst einmal die Verteilung der Kraftwerte betrachtet. Eine einfache Möglichkeit, die Kraft, eine numerische Variable, darzustellen, ist in Form einer Tabelle (siehe Tabelle 8.1).
| ID | Kraft[N] |
|---|---|
| P01 | 2414 |
| P02 | 2462 |
| P03 | 2178 |
| P04 | 2013 |
| P05 | 2194 |
| P06 | 2425 |
| P07 | 2305 |
| P08 | 2117 |
| P09 | 2298 |
| P10 | 2228 |
| P11 | 2243 |
| P12 | 2497 |
| P13 | 1800 |
| P14 | 2152 |
| P15 | 2089 |
| P16 | 2090 |
| P17 | 3200 |
| P18 | 2196 |
| P19 | 2485 |
| P20 | 2440 |
Selbst bei \(20\) Werten ist die Darstellung der Rohwerte mittels einer Tabelle allerdings leider wenig übersichtlich. Die Werte müssen Zeile für Zeile in der Tabelle durchgegangen werden und spezifische Kennwerte müssen notiert werden, um Vergleiche zwischen den Werten durchführen zu können. Beispielsweise zeigt die Tabelle, dass der Maximalwert der Beinkraft bei \(3200\)N für P17 und der Minimalwert von P13 bei \(1800\)N liegen. Aber wirklich übersichtlich ist die Darstellung in Form einer Tabelle nicht. Für solche univariaten Daten (uni = eins) kann eine übersichtlichere Darstellung mittels eines sogenannten Dotplots erreicht werden (siehe Abbildung 8.2).

Der Dotplot erlaubt deutlich einfacher sich einen Überblick über die Daten zu verschaffen. Beispielsweise welchen Wert das Minimum bzw. das Maximum annimmt ist direkt ersichtlich. Die grafische Darstellung erlaubt weiterhin direkt abzuschätzen, in welchem Wertebereich der Großteil der Daten liegt. Allerdings wird durch diese Art der Darstellung die Information darüber, welche Person die jeweiligen Werte besitzt, nicht mehr dargestellt. Dies stellt jedoch nicht zwingend ein Problem dar, da in den meisten Fällen sowieso Aussagen über die Gruppe und weniger über einzelne Personen gemacht werden sollen. Ein Dotplot hat gleichzeitig den Vorteil, dass die Verteilung der Werte abgeschätzt werden kann. In welchem Bereich liegen die meisten Datenwerte? Liegen die Werte eng beieinander oder streuen die Werte sehr stark? Gibt es einzelne Werte, die sehr unterschiedlich von den anderen Werten sind? Dies sind alles Fragen, die notwendig sind, um einen Datensatz und dessen Eigenschaften beurteilen zu können. Generell erfordert es etwas Erfahrung und Ausprobieren um eine effektive Darstellung der Daten zu finden. Dies hängt auch oft mit der Fragestellung zusammen, da unterschiedliche Darstellungen üblicherweise auch unterschiedliche Aspekte der Daten betonen bzw. in den Hintergrund rücken.
Zurück zum Kraftexperiment. Da in der kleinen Welt nur evidenzbasierte Entscheidungen getroffen werden, soll empirisch überprüft werden, ob das neue Training wirklich zu einer Verbesserung der Beinkraft führt. Um das Experiment zu vereinfachen, und da es sich mehr um ein Gedankenexperiment handelt, sei von von einem perfekten Krafttraining ausgegangen. Das heißt, Intervention ist dahingehend perfekt, dass die Intervention zu der gleichen Verbesserung bei allen Teilnehmerinnen und Teilnehmern führt. Dies ist natürlich eine unrealistische Annahme aber sie vereinfacht die Problembetrachtung bzw. Problemanalyse und ändert tatsächlich zunächst auch nichts an der inhaltlichen Problemstellung.
Das Beinkrafttraining sei also perfekt und verbessert die Kraftleistung um einen einzigen präzisen Wert. Sei die Verbesserung mit \(+100\)N gegeben. Dieser Kraftzuwachs ist unabhängig davon, welche Person aus der Population das Training durchführt. Um die Effektivität des Trainings abzuschätzen, sollen nun zwei Gruppen miteinander verglichen werden: eine Interventionsgruppe, welche das Krafttraining durchläuft, und eine Kontrollgruppe. In beiden Gruppen sollen jeweils \(n_{\text{TRT}} = n_{\text{CON}} = 3\) Teilnehmerinnen bzw. Teilnehmer einbezogen werden. Die Kontrollgruppe führt ebenfalls ein Krafttraining durch. Das Krafttraining der Kontrollgruppe sei aber perfekt uneffektiv. D.h. es das Training führt zu keiner Verbesserung der Kraftfähigkeiten der Teilnehmerinnen und Teilnehmer. Um das Experiment besser zu charakterisieren, sind allerdings erst noch ein paar Begrifflichkeiten notwendig.
Definition 8.2 (Abhängige Variable ) Die abhängige Variable ist diejenige Variable, die in einer Studie beobachtet, gemessen oder analysiert wird. Die abhängige Variable wird oft als “Effekt” betrachtet.
Definition 8.3 (Unabhängige Variable ) Die unabhängige Variable ist die Variable, die in einer Studie oder einem Experiment manipuliert oder kontrolliert wird. Die unabhängige Variable wird oft als “Ursache” betrachtet, da sie den potenziellen Einfluss auf die abhängige Variable repräsentiert.
Bezogen auf das vorliegende Experiment stellt die Gruppenzugehörigkeit somit die unabhängige Variable dar, während die Beinkraft die abhängige Variable darstellt. In dem Experiment wird somit der Effekt der Gruppenzugehörigkeit auf die Beinkraft untersucht. Die Zugehörigkeit zu einer der beiden Gruppe ist die Ursache für mögliche Effekte auf die Beinkraft.
Im folgenden wird nun so getan, als ob die Daten aus dem Zensus nicht vorliegen würden. Es stellen sich nun zwei Fragen: 1) Wie werden die sechs Personen aus der Population ausgewählt, und 2) wenn sechs Personen ausgewählt worden sind, wie werden diese Personen in die beiden Gruppen aufgeteilt?
Bezogen auf die zweite Frage, könnte eine Möglichkeit sein, die ersten drei Personen der Interventionsgruppe zuzuteilen und die verbleibenden drei Personen der Kontrollgruppe zuzuweisen. Implizit ist dabei festgelegt, dass die beiden Gruppen die gleiche Größe haben. Dies soll auch in der weiteren Diskussion beibehalten werden. Bei dieser sequentiellen Zuweisung kann es allerdings passieren, dass wenn die Personen in irgendeiner Form nach der Beinkraft schon vorsortiert sind, z.B. allgemeiner Gesundheitsstatus, Arbeitstätigkeit usw., dann würde sich diese Sortierung auf die Gruppen übertragen. Wenn die Personen von schwächer nach stärker sortiert sind, würden in der Interventionsgrupps die insgesamt schwächere Personen zugeteilt werden als in der Kontrollgruppe. Die initiale Beinkraft würde dann die Funktion einer sogenannten Störvariable einnehmen. Die Störvariable würde dazu führen, das das Ergebnis verfälscht würde.
Definition 8.4 (Störvariable) Eine Störvariable ist eine Variable, die einen Einfluss auf die abhängige Variable hat, deren Einfluss jedoch nicht kontrolliert wurde. Eine Störvariable ist nicht von Hauptinteresse für die Untersuchung.
In realen Fällen kann davon ausgegangen werden, dass immer eine ganze Reihe von Störvariablen vorliegen. Unglücklicherweise gehören dazu auch Störvariablen, die gar nicht bekannt sein müssen. Beispielsweise genetische Prädispositionen die noch nicht erforscht sind oder vielleicht noch nicht gemessen werden können. Daher wird ein Mechanismus benötigt der dafür sorgt, dass die Störvariablen möglichst wenig Einfluss auf den gesuchten Effekt ausüben. D.h. die Teilnehmerinnen und Teilnehmer müssen so den beiden Gruppen zugewiesen werden, dass die Störvariablen möglichst in gleichen Anteilen in den beiden Gruppen vorkommen. Der Mechanismus der dazu verwendet wird ist eine zufällige Zuteilung der Personen in die beiden Gruppen. Es wird eine Randomisierung durchgeführt.
Definition 8.5 (Randomisierung ) Mit Randomisierung wird der Prozess der zufälligen Zuweisung von Probanden oder Elementen zu verschiedenen Gruppen oder Bedingungen in einem Experiment bezeichnet. Die Randomisierung wird verwendet, um sicherzustellen, dass die Auswahl und Zuordnung der Elemente frei von systematischer Beeinflussung erfolgt.
Mit Hilfe der Randomisierung kann sichergestellt werden, dass im Mittel die Störvariablen gleichmäßig auf die beiden Gruppen verteilt sind. Ohne diese Annahmen, dass die Störvariablen gleichmäßig verteilt sind, ist es nicht möglich eine ursächliche Beziehung zwischen der abhängigen und der unabhängigen Variablen zu etablieren. Sind die Störvariablen nicht gleich verteilt, dann könnte ein möglicher Unterschied zwischen den Variablen auch nur auf Grund der Störvariablen zustande kommen. Die Randomisierung der Stichprobe in die Gruppen ist natürlich kein \(100\%\) Verfahren. Per Zufall kann es dazu kommen, dass Störvariablen nicht gleichmäßig verteilt sind, was bei unbekannten Störvariablen, auch nicht zu überprüfen ist. Dieses Problem wird umso größer umso kleiner die Anzahl der Personen ist. Seine zum Beispiel \(10\) Personen gegeben, von denen \(3\) Personen Merkmal A haben und \(7\) Personen Merkmal B. Die Wahrscheinlichkeit dafür, dass alle As der gleichen Gruppe zugeteilt werden liegt bei knapp \(17\%\). Bei dem gleichen Verhältnis mit \(100\) Personen und zwei Gruppen à \(50\) Personen ist die Wahrscheinlichkeit nur noch \(3.2e-10\). Damit ist die zweite Frage der Zuteilung beantwortet. Bleibt noch die Frage wie die sechs Personen aus der Population ausgewählt werden sollen.
Letztendlich ist bei der Auswahl der Stichprobe ein ähnliches Problem wie bei der Zuteilung in die beiden Gruppen zu lösen. Allerdings aus einer etwas anderen Perspektive. Die Ergebnisse die anhand der Stichprobe beobachtet werden, sollen letztendlich auf die Gesamtpopulation übertragen werden. D.h. wenn in der Population die eine Hälfe Merkmal A trägt und die andere Merkmal B und in der Stichprobe nur Personen mit Merkmal A sind, dann wird es schwierig bis unmöglich werden, das Ergebnis auf basierend auf der Stichprobe auf die Population zu übertragen. D.h. bei der Wahl der Stichprobe muss darauf geachtet werden, dass diese Stichprobe tatsächlich repräsentativ für die Population ist. Hier ist wieder das gleich Problem vorhanden, dass a-priori nicht klar ist, welche Merkmale relevant sind, daher können diese Merkmale auch nicht alle bestimmt werden und somit sichergestellt werden, dass die Merkmale in gleichem Maße in der Stichprobe repräsentiert sind, wie in der Population. Wieder ist die Lösung für das Problem eine Anwendung des Zufalls, nämlich indem eine sogenannte Zufallsstichprobe gewählt wird. Formaler:
Definition 8.6 (Stichprobe) Eine Stichprobe ist eine Teilmenge von Objekten aus der Population.
Definition 8.7 (Zufallsstichprobe) Eine Zufallsstichprobe ist eine Teilmenge von Objekten aus der Population, die zufällig ausgewählt wurde.
Bei der Zufallsstichprobe haben alle Personen in der Population vor dem Experiment die gleiche Wahrscheinlichkeit, gezogen zu werden. Dadurch kann sichergestellt werden, dass in der Stichprobe unterliegende Störvariablen, ob messbar oder nicht messbar, ebenso in der Stichprobe verteilt sind.
Eine kleine Simulation veranschlicht das Prinzip. Sei eine Population der Größe \(N = 100\) gegeben, in der \(30\) Objekte das Merkmal A haben und \(70\) Objekte das Merkmal B. Es werden nun wiederholt Zufallsstichproben der Größe \(N = 20\) aus dieser Population gezogen und für jede Stichprobe wird der Anteil der As berechnet.
In R lässt sich eine solche Simulation relativ einfach umsetzen, die hier der Übersicht halber \(20\) mal durchgeführt wird.
pop <- rep(c("A","B"), c(30,70))
n_sam <- 20
res <- numeric(n_sam)
for (i in 1:n_sam) {
sam <- sample(pop, 20)
res[i] <- mean(sam == 'A')
}
res [1] 0.30 0.40 0.30 0.35 0.10 0.30 0.30 0.25 0.15 0.30 0.50 0.30 0.30 0.40 0.25
[16] 0.30 0.20 0.35 0.25 0.35Wir die Ausgabe von res zeigt, dass tatsächlich in den meisten Fällen der Anteil von As in der Stichprobe in der Nähe der \(30\%\) aus der Population liegt. Nicht in allen Fällen, es gibt Schwankungen um diesen Wert herum, aber im Großen und Ganzen spiegelt die Stichprobe in Bezug auf die Verteilung von Merkmalen A und B die Population gut wieder. Das heißt, es handelt sich um eine repräsentative Stichprobe.
In Abhängigkeit von der Forschungsfragestellung kann die Anzahl der Merkmale relativ schnell anwachsen, in diesem Fall spielt die Größe der Stichprobe ebenfalls eine wichtige Rolle. Seien zum Beispiel für eine Fragestellung möglicherweise \(15\) Merkmale wie Alter, Geschlecht, sportliche Aktivität usw. relevant und es wird eine Stichprobe mit \(N = 16\) gewählt, dann ist es natürlich gar nicht möglich die Merkmale selbst wenn bekannt gleichmäßig in zwei Gruppen zu unterteilen. Daher ist die Repräsentativität einer solchen Stichprobe nur sehr eingeschränkt.
Zurück zum Kleine Welt Beispiel. Um jetzt für das Experiment eine Stichprobe zu ermitteln, wird genutzt, dass die Population bereits durchnummeriert ist. Nun kann eine Zufallszahlengenerator verwendet werden, der zunächst sechs Zahlen für die Stichprobe bestimmt. Beispielsweise die Zahlen \(i = \{3,7,8,9,10,20\}\). Die entsprechenden Personen werden aus der Population anhand der ID ausgewählt. Anschließend teilt wieder ein Zufallszahlengenerator die sechs Personen in die beiden Gruppen auf (siehe Abbildung 8.3).
flowchart TD
A{Population} --> B(Zufallszahlengenerator)
B --> C[Stichprobe]
C --> D(Zufallszahlengenerator)
D --> E[Kontrollgruppe]
D --> F[Interventionsgruppe]
Wie bereits hergeleitet, ist dieser Prozess der zufälligen Ziehung und zufälligen Zuteilung kritisch, um das Ergebnis des Experiments eindeutig interpretieren zu können und eine Generalisierung über die bestehenden Objekte hinaus durchführen zu können. Leider ist der erste Schritt, die zufällige Ziehung von Objekten aus der Population, in der Realität nur sehr schwer realisierbar.
In Tabelle 8.2 ist die Stichprobe und Zuteilung in die Gruppen zu sehen.
| ID | Kraft[N] | Gruppe |
|---|---|---|
| P08 | 2117 | CON |
| P09 | 2298 | CON |
| P03 | 2178 | CON |
| P07 | 2305 | TRT |
| P10 | 2228 | TRT |
| P20 | 2440 | TRT |
Mit diesen sechs Personen sollen nun das Experiment durchgeführt werden. Die drei Personen aus der Kontrollgruppe durchlaufen im Interventionszeitraum nur ein Standardtraining, während die Interventionsgruppe zweimal die Woche für 12 Wochen das perfekte Krafttraining durchführt. Nach diesem Zeitraum wird die Beinkraft aller Personen aus beiden Gruppen gemessen. Es wird das folgende Ergebnis erhalten (siehe Tabelle 8.3). Es sei angenommen, dass die Werte aus dem Zensus nicht bekannt sind.
| ID | Kraft[N] |
|---|---|
| P08 | 2117 |
| P09 | 2298 |
| P03 | 2178 |
| \(\bar{K}\) | 2198 |
| ID | Kraft[N] |
|---|---|
| P07 | 2405 |
| P10 | 2328 |
| P20 | 2540 |
| \(\bar{K}\) | 2424 |
Für beide Gruppen ist in Tabelle 8.3 jeweils noch der Mittelwert \(\bar{K}\) dokumentiert, um die Gruppen leichter miteinander vergleichen zu können. Später werden noch weitere Maße eingeführt, die es ermöglichen, zwei Mengen von Werten miteinander zu vergleichen. Der Mittelwert ist ein Maß, dass aber schon bekannt sein sollte.
Definition 8.8 (Mittelwert) Der Mittelwert \(\bar{x}\) über \(n\) Werte berechnet sich nach der Formel:
\[ \bar{x} = \frac{\sum_{i=1}^n x_i}{n} \tag{8.1}\]
Der Mittelwert wird mit einem Strich über der Variable dargestellt.
Wenn die Schreibweise mit dem Summenzeichen \(\Sigma\) etwas verwirrend erscheind, dann sind im Anhang noch mal die wichtigsten Infos zum Rechnen mit Summen angegeben. Mit dem Mittelwert ist auch gleichzeitig das zentrale und namensgebende Konzept aus der Statistik eingeführt worden. Die Statistik. Ein Wert, der mittels der Werte aus einer Stichprobe berechnet wird, wird als Statistik bezeichnet.
Definition 8.9 (Statistik) Ein auf einer Stichprobe berechneter Wert wird als Statistik bezeichnet.
Der Definition folgend, ist somit der Mittelwert \(\bar{X}\) einer Stichprobe eine Statistik. Das Gleiche würde gelten, wenn anstatt des Mittelwerts der Maximalwert oder der Minimalwert einer Stichprobe ermittelt wird. Da beide Werte anhand der Werte aus der Stichprobe berechnet werden, stellen der Maximalwert und der Minimalwert ebenfalls eine Statistik dar.
Um nun den Unterschied zwischen den beiden Gruppen zu bestimmen, gibt es eine ganze Reihe von verschiednen Ansätzen. Ein sehr direkte und auch intuitiv nachvollziehbare Möglichkeit ist die Differenz \(D\) zwischen den beiden Mittelwerten zu berechnen. Dabei ist es notwendig eine Richtung zu bestimmen bzw. welcher der beiden Mittelwerte den Minuenden und welcher den Subtrahenden darstellt. Hier gibt es keine Vorgaben, sondern die Richtung kann frei bestimmt werden und muss nur entsprechend dokumentiert werden. Im vorliegenden Fall soll die Interventionsgruppe von der Kontrollgruppe abgezogen werden. Da ausgegangen wird, dass die Intervention zu einer Krafterhöhung führt sollte mit dieser Konvention ein positiven Unterschied erhalten werden. Dies führt dann zur Definition \(\eqref{eq-sts-basics-ex1-d}\).
\[\begin{equation} D := \bar{K}_{\text{TRT}} - \bar{K}_{\text{CON}} \label{eq-sts-basics-ex1-d} \end{equation}\]
Für das Beispiel des kleine Welt Experiment werden dementsprechend der folgenden Wert erhalten:
\[ D = 2424N - 2198N = 226 N \]
Da der Wert \(D\) wiederum auf den Daten der Stichprobe berechnet wird, handelt es sich ebenfalls um eine Statistik.
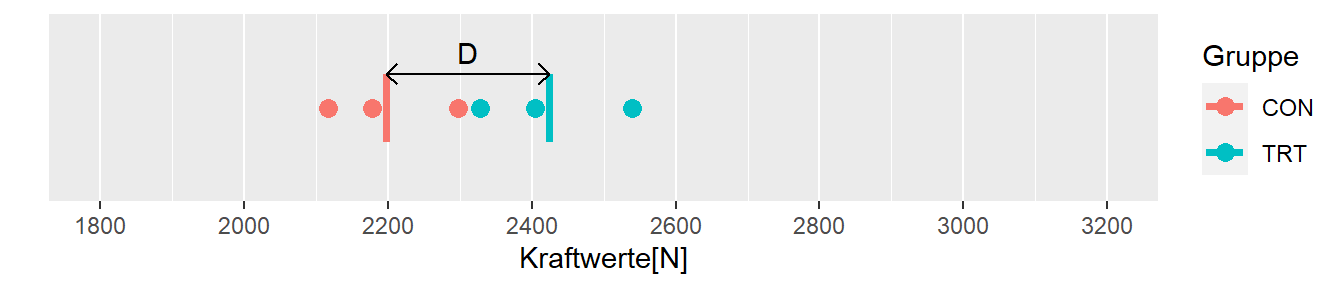
In Abbildung 8.4 sind die Werte der beiden Gruppen, deren Mittelwerte \(\bar{K}_{\text{CON}}\) und \(\bar{K}_{\text{TRT}}\) und der Unterschied \(D\) zwischen diesen graphisch abgetragen. Wie erwartet zeigt die Interventionsgruppe den höheren Kraftwert im Vergleich zu der Kontrollgruppe. Allerdings ist der Wert mit \(D = 226\) größer als der tatsächliche Zuwachs von \(\Delta_{\text{Training}} = 100\). Der Unterschied zwischen den beiden Gruppen ist natürlich auch zum Teil auf die Unterschiede, die zwischen den beiden Gruppen vor der Intervention bestanden haben, zurückzuführen. Dies führt zu der Frage was denn passiert wäre, wenn eine andere Stichprobe gezogen worden wäre?
Sei \(i = \{12,2,19,4,8,16\}\) eine zweite Zufallsstichprobe. Dies würde zu den folgenden Werten nach der Intervention führen.
| ID | Kraft[N] | Gruppe |
|---|---|---|
| P12 | 2497 | CON |
| P02 | 2462 | CON |
| P19 | 2485 | CON |
| P04 | 2113 | TRT |
| P08 | 2217 | TRT |
| P16 | 2190 | TRT |
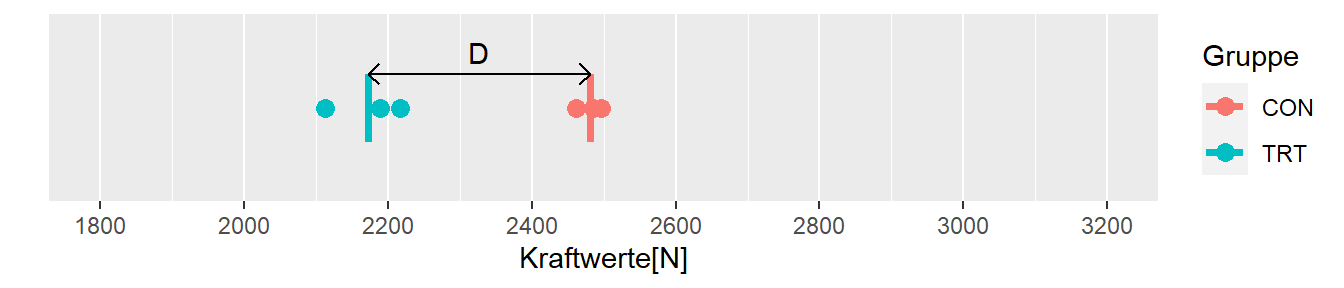
In Abbildung 8.5 sind wieder die Datenpunkte, Mittelwerte und der Unterschied in den Mittelwerten zwischen den beiden Gruppen abgetragen. In diesem Fall ist allerdings die Differenz zwischen den beiden Gruppen genau in der anderen Richtung \(D = -308\). Daher würde dieses Ergebnis tatsächlich genau in der anderen Richtung hin interpretiert werden. Das Krafttraining führt nicht nur zu keiner Verbesserung in der Kraftfähigkeit, sondern sogar zu einer Verschlechterung!
Es hätte aber auch sein können, dass noch eine andere Stichprobe gezogen worden wäre, z.B. \(i = \{6,5,7,20,14,16\}\). Mit dieser Stichprobe würden das folgende Ergebnis beobachtet werden (siehe Tabelle 8.5).
| Gruppe | Kraft[N] |
|---|---|
| CON | 2308 |
| TRT | 2327 |
| \(D\) | 19 |
In diesem Fall haben ist zwar ein positiver Unterschied zwischen den beiden Gruppen in der zu erwartenden Richtung gefunden worden, der Unterschied von \(D = 19\) ist allerdings deutlich kleiner als der tatsächliche Unterschied \(\Delta = 100\). Daher könnte das Ergebnis möglicherweise so interpretieren werden, das das Krafttraining als ineffektiv bewertet wird und keine Empfehlung für das Training ausgesprochen wird.
Zu beachten ist, dass keines der Ergebnisse 100% korrekt ist. Entweder ist der Unterschied zwischen den beiden Gruppen deutlich zu groß, in der falschen Richtung oder deutlich zu klein. Das Ergebnis des Experiments hängt ursächlich damit zusammen, welche Zufallsstichprobe gezogen wurde und wie diese Stichprobe in die Gruppen unterteilt wird. Denn natürlich würden sich die \(D\)-Werte ebenfalls ändern, wenn die Stichprobe gleich gehalten würde aber die Zuteilung geändert wird. Daraus folgt, dass bei Wiederholungen des Experiments generell jeweils unterschiedliche Werte beobachtet werden und dieses Phänomen ist eine Folge der notwendigen Randomisierungsschritte. Allgemein wird das Phänomen, dass der Wert der berechneten Statistik zwischen Wiederholungen des Experiments schwankt, als Stichprobenvariabilität bezeichnet.
Definition 8.10 (Stichprobenvariabilität) Durch die Anwendung von Zufallsstichproben variiert eine auf den Daten berechnete Statistik. Diese Variabilität wird als Stichprobenvariabilität bezeichnet.
Streng genommen führt die Stichprobenvariabilität allein noch nicht dazu, dass sich die Statistik zwischen Wiederholungen des Experiments verändert, sondern die zu untersuchenden Werte in der Population müssen selbst auch eine Streuung aufweisen. Wenn eine Population untersucht würde, bei der alle Personen die gleiche Beinkraft hätten, würden unterschiedliche Stichproben immer den gleichen Mittelwert haben und wiederholte Durchführungen des Experiments würden immer wieder zu demselben Ergebnis führen. Dieser Fall ist in der Realität jedoch praktisch nie gegeben, und sämtliche interessante Parameter zeigen immer eine natürliche Streuung in der Population. Diese Streuung in der Population führt daher zu dem besagten Phänomen, dass das gleiche Experiment mehrmals wiederholt zu unterschiedlichen Zufallsstichproben und dementsprechend immer zu unterschiedlichen Ergebnissen führt. Das Ergebnis ist inhärent variabel bzw. unsicher. Dieses grundlegende Prinzip liegt allen Datenanalysen zugrunde. Bei nicht-experimentellen Daten ergeben sich noch weitere Probleme, im weiteren wird aber vor allem die experimentelle Herangehensweise mit randomisierten Experimenten behandelt, da dieses die dominante Herangehensweise darstellen kausale Effekte zwischen abhängigen und unabhängigen Variablen zu erstellen. Die zentrale Aufgabe der Disziplin Statistik ist somit mit dieser Variabilität umzugehen und Forscherinnen in die Lage zu versetzen, trotz dieser Unsicherheit rationale Entscheidungen zu treffen.
Eine implizite Kernannahme bei diesem Ansatz ist, dass mit Hilfe von Daten überhaupt etwas über die Welt erlernt werden kann. Das heißt, dass die Erhebung von Daten einen in die Lage versetzt, rationale Entscheidungen zu treffen. Entscheidungen wie ein spezialisiertes Krafttraining mit einer klinischen Population durchzuführen oder eine bestimmte taktische Variante mit meiner Mannschaft zu trainieren, um die Gegner besser auszuspielen. Alle diese Entscheidungen sollten rational vor dem Hintergrund von Variabilität und Unsicherheit getroffen werden und zwar möglichst so, das möglichst oft korrekte Entscheidungen getroffen werden. Wie noch gezeigt wird, kann auch die Statistik leider nicht garantieren, dass immer die korrekte Entscheidung getroffen wird. Es kann auch mal vorkommen, dass beim Würfelwurf zehnmal hintereinander ein sechs gewürfelt wird, ohne dass der Würfel in irgendeiner Art und Weise manipuliert wurde. Nochmals auf den Punkt gebracht nach Wild und Seber (2000, p.28):
The subject matter of statistics is the process of finding out more about the real world by collecting and then making sense of data.
Sei zunächst noch einmal das Phänomen weiter untersucht, dass Wiederholungen desselben Experiments zu unterschiedlichen Ergebnissen führen. Im Beispiel liegt der unrealistische Vorteil vor, dass die tatsächliche Wahrheit bekannt ist. Dieser Umstand soll nun verwendet werden. In Abbildung 8.6 ist die Verteilung der drei bisherigen \(D\)s abgetragen.
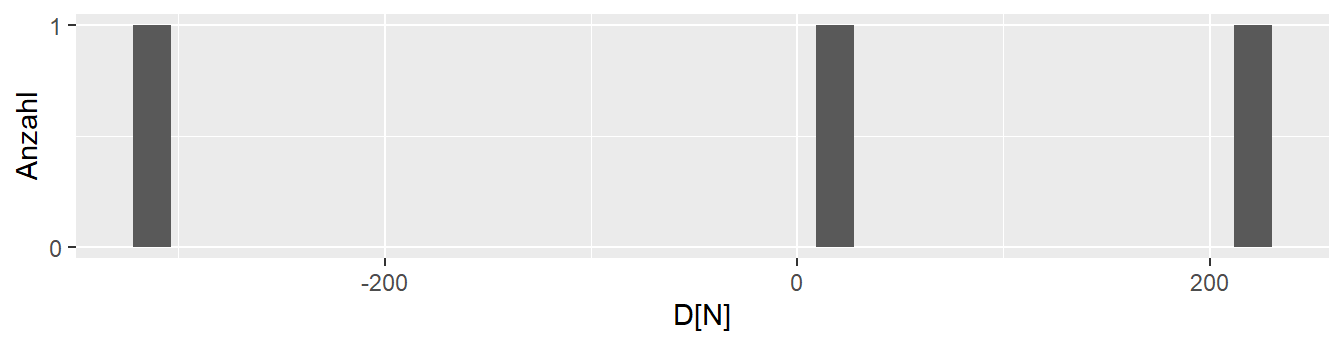
Die drei Werte liegen relativ weit auseinander. Eine Anschlussfrage könnte daher sein: “Welche weiteren Werte sind denn überhaupt mit der vorliegenden Population möglich?”.
8.2 Die Stichprobenverteilung
Um die Frage zu beantworten, kann das Experiment einfach noch mehrere Male wiederholt werden. In Abbildung 8.7 sind dazu \(15\) weitere Zufallsstichproben abgetragen. In jeder Zeile sind alle \(20\) Personen der Population angetragen und die sechs jeweils gezogenen TeilnehmerInnen sind farbig markiert. Drei für die Kontrollgruppe und drei für die Interventionsgruppe. Für jede dieser Zeilen können nun wieder die Gruppenmittelwerte berechnet und der Unterschied \(D\) bestimmen werden.
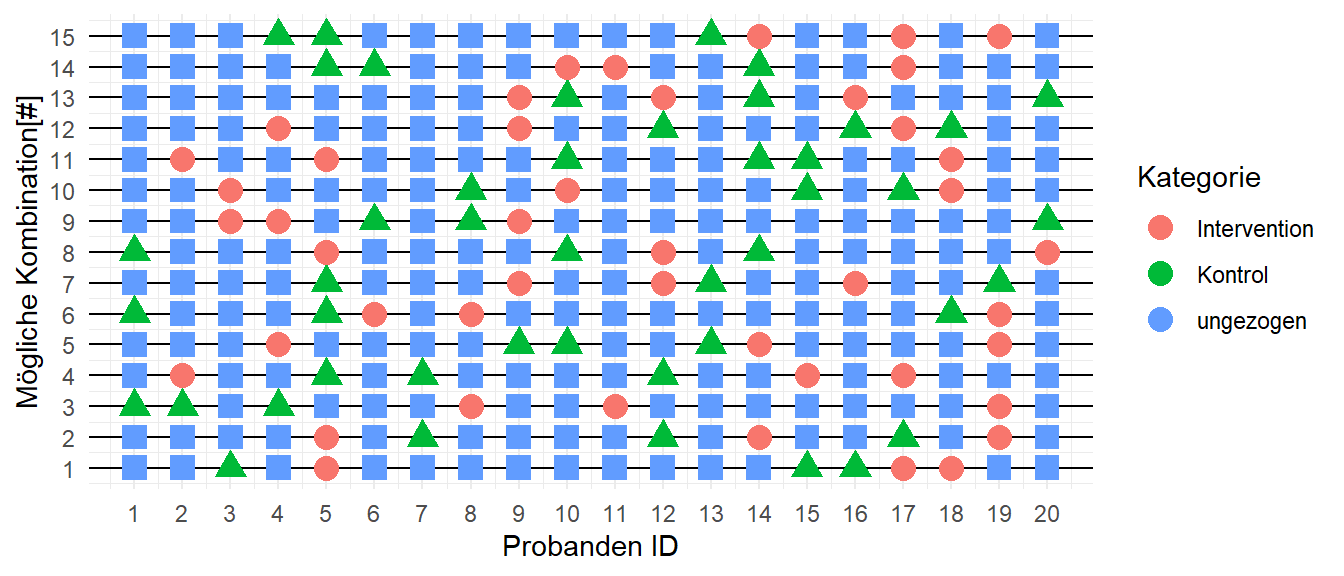
Tatsächlich ist es nicht notwendig sich nur auf \(15\) Zufallsstichproben zu beschränken. Dadurch, dass die Population relativ übersichtlich ist, ist es relativ einfach möglich alle Möglichkeiten zu ermitteln. Die Herleitung benötigt allerdings etwas Mathematik aus der Schule, im speziellen die Kombinatorik, die sich mit dem Zählen von Möglichkeiten befasst. Beispielsweise mit der Frage, wie viele Möglichkeiten es gibt aus einer Urne mit \(20\) nummerierten Kugeln sechs Kugeln zu ohne Zurücklegen zu ziehen. Eine direkte Herleitung könnte so gehen. Bei sechs Kugeln ohne zurückziehen, kann die erste Kugel \(20\) unterschiedliche Werte haben, die zweite \(19\) unterschiedliche Werte, da eine Kugel schon entnommen wurde, die dritte Kugel hat \(18\) mögliche Werte usw bis zur sechsten Kugel für die es \(15\) Möglichkeiten gibt.
\[\begin{equation*} \text{Möglichkeiten} = 20 \cdot 19 \cdot 18 \cdot 17 \cdot 16 \cdot 15 \end{equation*}\]
Mit der Definition der Fakultät \(!\),
\[\begin{equation*} n! = n \cdot (n-1) \cdot (n-2) \cdots 1 \end{equation*}\]
kann dies kürzer geschrieben werden mit:
\[\begin{equation*} \text{Möglichkeiten} = \frac{20!}{(20-6)!} = \frac{20!}{14!} \end{equation*}\]
Da die Reihenfolge der Ziehung keine Rolle spielt müssen noch zum Beispiel die Fälle \([1,2,3,4,5,6]\) und \([2,3,4,5,6,1]\) und alle weiteren Permutationen der Menge \(\{1,2,3,4,5,6\}\) berücksichtigt werden. Hier funktioniert auch wieder das Abzählverfahren von eben. Wenn die sechs Kugel gezogen wurden und es sind sechs freie Plätze vorhanden, dann kann der erste Platz mit sechs Kugeln belegt werden, der zweite Platz mit fünf Kugeln, der dritte Platz mit vier Kugeln usw.. Das heißt es ergibt sich insgesamt:
\[\begin{equation*} \text{Permutationen} = 6 \cdot 5 \cdot 4 \cdot 3 \cdot 2 \cdot 1 = 6! \end{equation*}\]
D.h. die oben hergeleitete Anzahl von Möglichkeiten muss noch durch diese Anzahl der Permutationen geteilt werden um insgesamt die Anzahl der Möglichkeiten sechs Kugeln aus zwanzig Kugeln ohne zurücklegen und ohne Rücksicht auf die Reihenfolge zu bestimmten.
\[\begin{equation*} \text{Möglichkeiten sechs aus zwanzig} = \frac{20!}{14!6!} = 3.876\times 10^{4} \end{equation*}\]
Wenn der Ansatz verallgemeinert wird mit \(N = 20\) und \(K = 6\) folgt daraus die Formel für den sogenannten Binomialkoeffizienten der als \(N\) über \(K\) gelesen wird.
\[\begin{equation} \text{Anzahl} = \binom{N}{K} = \frac{N!}{K!(N-K)!} \label{eq-binom-coef} \end{equation}\]
Die Anzahl der Möglichkeiten sechs aus zwanzig zu ziehen ist damit hergeleitet. Es fehlt noch die Aufteilung in die beiden Gruppen. Sei dazu die Treamentgruppe betrachtet, d.h. aus den sechs gezogenen Personen (Kugeln) sollen drei in die Treatmentgruppe gesteckt werden. Wenn diese drei Personen bestimmt wurden, ist automatisch auch die Kontrollgruppe bestimmt und die Kontrollgruppe braucht nicht weiter betrachtet werden. Letztendlich ist diese Problemstellung genau wieder die gleiche wie auch bei der Ziehung der Stichprobe. Daher folgt mit \(N = 6\) und \(K = 3\).
\[\begin{equation*} \text{Gruppenzuteilung} = \binom{6}{3} = 20 \end{equation*}\]
Insgesamt folgt für die Anzahl der möglichen Stichprobenkombinationen somit:
\[\begin{equation*} \text{Anzahl} = \binom{20}{6}\binom{6}{3} = 7.752\times 10^{5} \label{eq-count-experiment} \end{equation*}\]
Dies sind natürlich selbst bei dieser kleinen Population eine große Menge an einzelnen Experimenten. Aber dafür sind Computer da (Stichwort for-Schleife). In R stellt diese Aufgabe kein Problem dar. In Abbildung 8.8 ist die Verteilung aller möglichen Experimentenausgänge, d.h. alle möglichen Differenzen \(D\) zwischen der Interventions- und der Kontrollgruppe, abgebildet.
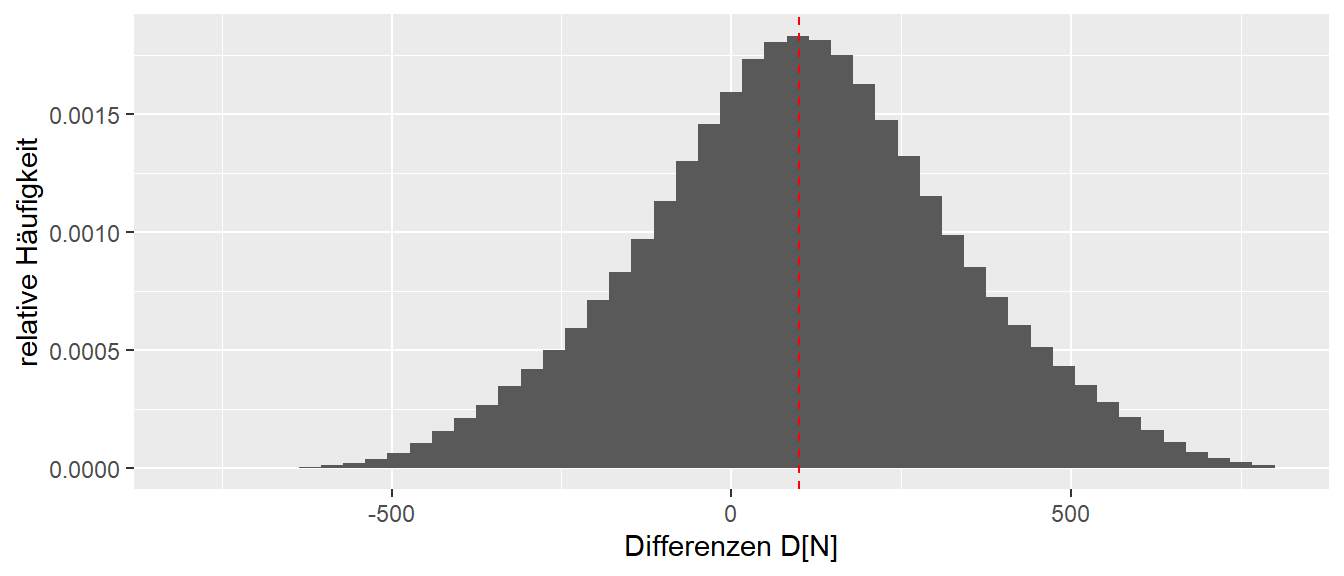
Auf der x-Achse sind die möglichen Differenzen \(D\) abgetragen, während auf der y-Achse die relative Häufigkeit, d.h. die Häufigkeit für einen bestimmten \(D\)-Wert geteilt durch die Anzahl \(7.752\times 10^{5}\) aller möglichen Werte. Diese Verteilung der Statistik \(D\)s wird als Stichprobenverteilung bezeichnet.
Definition 8.11 Die Stichprobenverteilung einer Statistik beschreibt die Verteilung der Statistik. Wenn beispielsweise die Statistik der Mittelwert \(\bar{x}\) ist, dann beschreibt die Stichprobenverteilung die Verteilung der möglichen Mittelwerte.
Abbildung 8.8 zeigt, dass die überwiegende Anzahl der Ausgänge tatsächlich auch im Bereich von \(\Delta = 100\) liegt. Noch präziser: Das Maximum der Verteilung, also die höchste relative Häufigkeit, liegt genau auf der roten Linie. Dies sollte tatsächlich etwas beruhigen, denn es zeigt, dass die Art der Herangehensweise mittels zweier Stichproben auch tatsächlich in den meisten Fällen einen nahezu korrekten Wert ermittelt. Allerdings zeigt die Stichprobenverteilung auch, dass Werte am rechten Ende, die deutlich zu hoch sind, wie auch Werte am linken Ende der Verteilung, die deutlich in der falschen Richtung liegen, möglich sind. Das bedeutet, wenn ein Experiment nur einziges Mal durchgeführt, kann man sich eigentlich nie sicher sein, welches dieser vielen Experimente durchgeführt wurde. Es ist zwar wahrscheinlicher, dass eines aus der Mitte der Verteilung durchgeführt wird, einfach da die Anzahl größer ist, aber es gibt keine 100%-ige Garantie, dass ein Experiment eine Niete ist und das Experiment ganz links mit \(D = -500\) oder aber auch Experiment ganz rechts mit \(D = 700\) durchgeführt wurde. Diese Unsicherheit kann leider keine Art von Experiment vollständig auflösen können. Eine weitere Eigenschaft der Verteilung ist ihre Symmetrie bezüglich des Maximums mit abnehmenden relativen Häufigkeiten, je weiter von Maximum \(D\) entfernt ist (Warum macht das heuristisch Sinn?).
Die Darstellungsform von Abbildung 8.8 wird als Histogramm bezeichnet und eignet sich vor allem dazu, die Verteilung einer Variablen z.B. \(x\) darzustellen. Dazu wird der Wertebereich von \(x\) zwischen dem Minimalwert \(x_{\text{min}}\) und dem Maximalwert \(x_{\text{max}}\) in \(k\) gleich große Intervalle unterteilt, und die Anzahl der Werte innerhalb jedes Intervalls wird abgezählt und durch die Anzahl der Gesamtwerte geteilt, um die relative Häufigkeit zu bestimmen.
Zum Beispiel für die Werte:
\[ x_i \in \{1,1.5,1.8,2.1,2.2,2.7,2.8,3.5,4 \} \]
könnte das Histogram ermittelt werden, indem der Bereich von \(x_{\text{min}} = 1\) bis \(x_{\text{max}} = 4\) in vier Intervalle unterteilt wird und dann die Anzahl der Werte in den jeweiligen Intervallen ermittelt wird (siehe Abbildung 8.9). Die ermittelte Anzahl würde dann noch durch die Gesamtanzahl \(9\) der Elemente geteilt um die relative Häufigkeit zu berechnen.
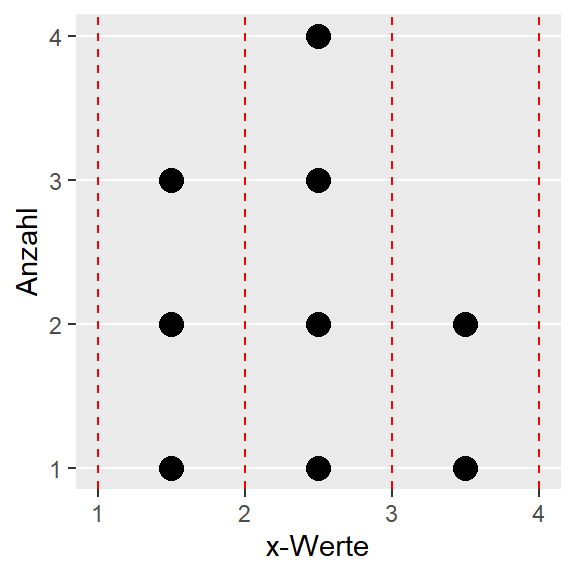
Die Form des Histogramms hängt davon ab, wie viele Intervalle verwendet werden. Die Auflösung wird mit mehr Intervallen besser, aber gleichzeitig verringert sich die Anzahl pro Intervall. Andersherum wird die Auflösung mit weniger Intervallen geringer, aber die Anzahl der Elemente pro Intervall wird größer und somit stabiler. Daher sollte in den meisten praktischen Fällen die Anzahl variiert werden, um sicherzugehen, dass nicht nur zufällig eine spezielle Darstellung gefunden wurde.
Wie bereits besprochen, sind alle Werte zwischen etwa \(D = -500N\) und \(D = 700\)N plausibel bzw. möglich nach Abbildung 8.8. Sei einmal betrachtet, was passiert, wenn das Training überhaupt nichts bringt und es keine Verbesserung gibt, also \(\Delta = 0\).
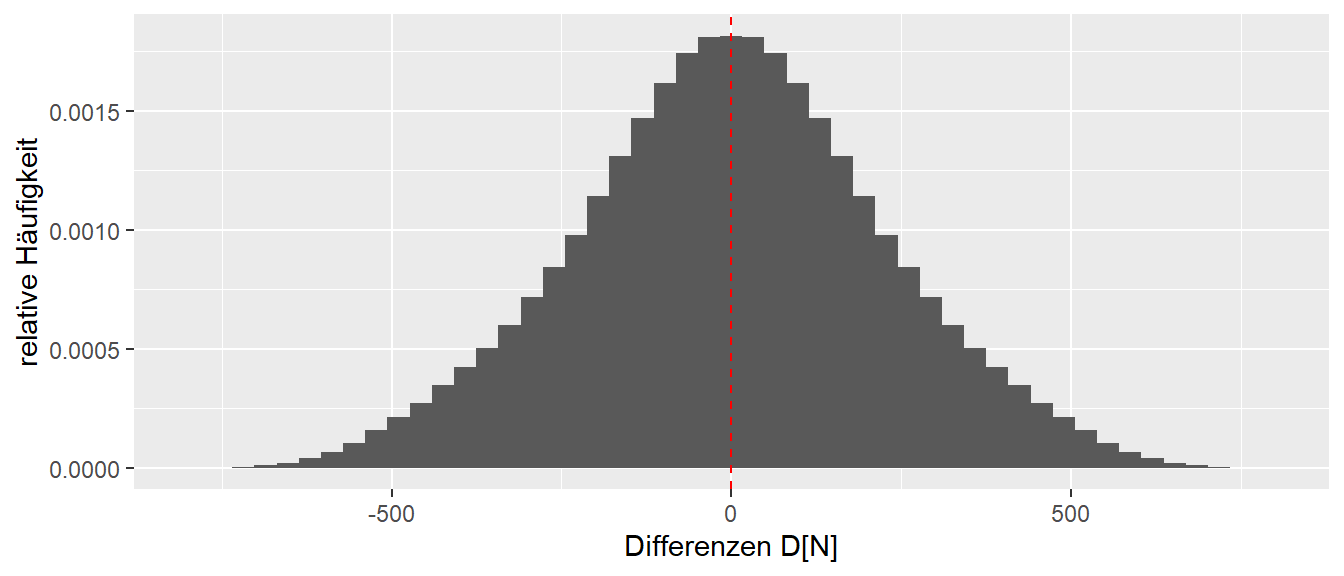
Die Verteilung in Abbildung 8.10 sieht praktisch genau gleich aus wie diejenige für \(\Delta = 100\). Der einzige Unterschied ist lediglich, dass sie nach links verschoben ist, und zwar scheinbar genau um die \(100\)N Unterschied zwischen den beiden \(\Delta\)s. Dies ist letztendlich auch nicht weiter verwunderlich, bei der Berechnung des Unterschieds \(D\) zwischen den beiden Gruppen kommen in beiden Fällen genau die gleichen Kombinationen vor. Bei \(\Delta = 100\) wird aber zu der Interventionsgruppe das \(\Delta\) addiert, bevor die Differenz der Mittelwerte berechnet wird. Da jedoch gilt:
\[ D = \frac{1}{3}\sum_{i=1}^3 x_{\text{KON}i} - \frac{1}{3}\sum_{j=1}^3 (x_{\text{TRT}j} + \Delta) = \bar{x}_{\text{KON}} - \bar{x}_{\text{TRT}} + \Delta \]
Daher bleibt die Form der Verteilung genau gleich und wird lediglich um den Wert \(\Delta\) im Vergleich zur Nullintervention nach rechts verschoben. Mit Nullintervention ist umgangssprachlich die Intervention gemeint, bei der nichts passiert, also \(\Delta = 0\) gilt.
Sei nun davon ausgegangen, dass eine dieser beiden Annahmen korrekt ist. Entweder ist die Intervention effektiv mit \(\Delta = 100\) oder die Intervention zieht keine Verbesserung nach \(\Delta = 0\). Wenn die beiden Verteilungen übereinander gelegt, entsteht die Abbildung Abbildung 8.11. Die Darstellungsform ist etwas verändert worden und eine Kurve wurde durch die relativen Häufigkeiten gelegt. Dieser Graph wird jetzt nicht mehr als Histogramm, sondern als Dichtegraph bezeichnet.
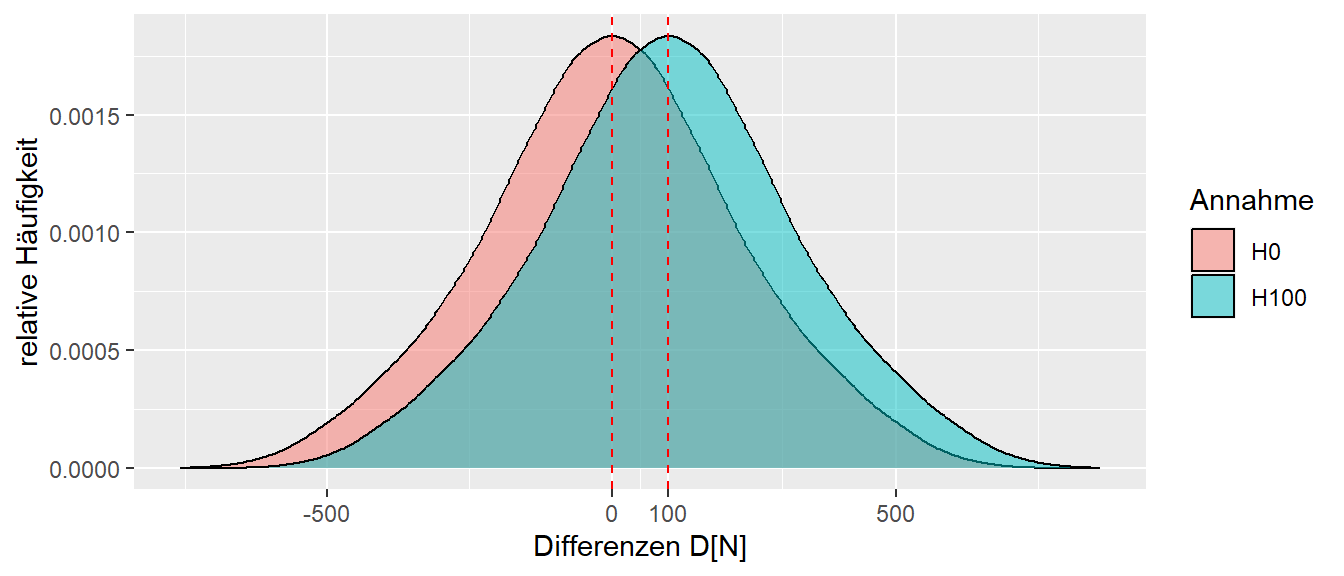
In Abbildung 8.11 ist klar zu sehen, dass die beiden Graphen zu großen Teilen überlappen. Dazu kommt weiterhin, dass die Überlappung in dem Bereich liegt, in dem beide Verteilungen ihre höchsten relativen Häufigkeiten haben. D.h. die Bereiche in die Verteilungen die größte Wahrscheinlichkeit haben beobachtbare Werte zu generieren. Das Problem besteht nun darin, dass bei der Durchführung eines Experiments nicht a-priori bekannt ist, welchen Effekt das Training auf die Stichprobe hat. Wenn der Effekt bereits bekannt wäre, dann müsste das Experiment gar nicht mehr durchgeführt werden. Nach der Durchführung des Experiments wird nun ein Unterschied \(d\) zwischen den beiden Gruppen betrachtet (siehe ?fig-sts-bascis-all-combinations-decision)

Sei zum Beispiel der Wert \(d = 50\) beobachtet. Dann entsteht ein Zuweisungsproblem (siehe Abbildung 8.12). Wie wird das beobachtete Ergebnis den beiden möglichen Realitäten zugewiesen? Einmal kann es sein, dass das Krafttraining nichts gebracht hat und lediglich eine der vielen möglichen Stichprobenkombinationen beobachtet wurde, die zu einem positiven Wert für \(D\) führen. Oder aber das Krafttraining ist effektiv gewesen und hat zu einer Verbesserung von \(\Delta = 100\)N geführt, und es wurde lediglich eine Stichprobenkombination gezogen, die zu einem Ergebnis von \(D = 50\) führt. In der Realität ist leider nicht bekannt, welche der beiden Annahmen korrekt ist, und es kann leider nie vollständig bekannt sein. Denn egal wie viele Experimente durchgeführt werden, es bleibt immer die Möglichkeit, dass zufällig nur Werte aus dem linken oder rechten Teil der Verteilung beobachtet wurden. Es ist eben auch mit einem fairen Würfel möglich zehnmal hintereinander eine sechs zu würfeln. Diese Unsicherheit lässt sich leider durch keine Art von Experiment vollständig auflösen.
Als Fazit sollte nun nachvollziehbar sein, dass jede Statistik, die auf einer Stichprobe berechnet wurde, inhärent unsicher ist. In der Realität ist der Sachverhalt noch komplexer und es tritt nicht nur die Variabilität aufgrund der Randomisierung auf, sondern es kommen viele weitere Einflussgrößen zum tragen, die das Ergebnis eines Experiments bei Wiederholungen beeinflussen können. Mithilfe einer statistischen Analyse wird nun versucht, diese Unsicherheit zu quantifizieren bzw. abzuschätzen und in den Entscheidungsprozesse auf der Basis der beobachteten Daten einfließen zu lassen. Die Methoden der Statistik liefern daher Werkzeuge an die Hand, um trotzdem rational zu entscheiden, welche Annahmen möglicherweise plausibler ist. Die statistische Analyse kann dabei immer nur etwas über die beobachteten Daten aussagen und nur indirekt etwas über die zugrundeliegenden wissenschaftlichen Theorien.
8.3 Things to know
- Population
- (Zufalls-)Stichprobe
- Randomisierung
- Statistik
- Stichprobenverteilung
- Abhängige und unabhängige Variable