| Velocity[m/s] | body mass[kg] | arm span[cm] |
|---|---|---|
| 15.8 | 70.7 | 189.2 |
| 17.2 | 63.7 | 182.0 |
| 18.3 | 76.2 | 192.1 |
| 18.4 | 64.9 | 171.1 |
| 18.4 | 63.0 | 181.1 |
17 Einführung
In den meisten Fällen in der Praxis liegt selten der einfache Fall vor, dass eine abhängige Variable mittels nur einer einzigen Prädiktorvariablen erklärt bzw. vorhergesagt werden soll. In den meisten Fällen liegt das Interesse darin den Zusammenhang mehrerer Prädiktorvariablen auf die abhängige Varible zu zu modellieren. Ein Beispiel aus der Literatur ist eine Untersuchung von Debanne und Laffaye (2011) über den Zusammenhang zwischen der Wurfgeschwindigkeit in Abhängigkeit vom Körpergewicht und der Armspannweite im Handball. In Tabelle 17.1 ist ein Ausschnitt aus dem Datensatz abgebildet.
Im Prinzip ändert sich an der Art der Daten nichts gegenüber der einfachen Regression. Die Daten beinhalten lediglich nun eine weitere Spalten mit einer weiteren Prädiktorvariablen. Im Prinzip könnte der isolierte Einfluss der beiden Prädiktorvariablen Körpermasse und Armspannweite auf die abhängige Variable Wurfgeschwindigkeit einzeln untersucht werden. Allerdings ist oft von größerem Interesse zu untersuchen, wie sich der gemeinsame Einfluss der beiden Variablen zusammen verhält und ob durch die Kombination der beiden Variablen ein besseres Modell erstellt werden kann. Aus dieser Problemstellung heraus ergibt sich die Notwendigkeit von der einfachen linearen Regression zur multiple lineare Regression überzugehen. Formal geschieht dies einfach dadurch, dass die Formel der einfachen Regression mit dem Prädiktor \(X\) um eine weitere oder eben mehrere Variablen erweitert wird. Dementsprechend wird aus:
\[\begin{equation} y_i = \beta_0 + \beta_1 x_i + \epsilon_i \end{equation}\]
die Formel für die multiple Regression mit:
\[\begin{equation} y_i = \beta_0 + \beta_1 x_{1i} + \beta_2 x_{2i} + \dots + \beta_K x_{Ki} + \epsilon_i \end{equation}\]
Da bei der einfachen Regression nur eine einzige \(X\)-Variable in der Formel vorhanden war, ist kein Index \(j\) notwendig gewesen um die \(X\)-Variablen voneinander zu unterscheiden. Bei der multiplen Regression mit mehreren Prädiktorvariablen \(X\) wird jeder \(X\) Variable ein zusätzlicher Index \(j\) angehängt um die Variablen eindeutig identifizieren zu können. Per Konvention, wobei diese leider nicht global eingehalten wird, wird die Anzahl der Prädiktorvaiablen mit \(K\) bezeichnet (oft auch \(p\)). Der \(y\)-Achsenabschnitt erhält wieder den Index \(j=0\) und die weiteren Steigungskoeffzienten \(\beta_1\) bis \(\beta_K\) erhalten den Prädiktorvariablen \(X_j\) folgend den entsprechenden Index.
In welcher Reihenfolge die Prädiktorvariablen mit \(j=1, j=2, \ldots, j=K\) verteilt werden hat zunächst keine Auswirkung auf das Modell und regelt lediglich die Bezeichnung. In unserem konkreten Fall der Handballwurfdaten wäre zum Beispiel eine mögliche Zuordnung, das \(X_1\) die Körpermasse und \(X_2\) die Armspannweite kodiert.
| \(i\) | Velocity[m/s] | body mass[kg] \(j=1\) | arm span[cm] \(j=2\) |
|---|---|---|---|
| 1 | 15.8 | 70.7 | 189.2 |
| 2 | 17.2 | 63.7 | 182.0 |
| 3 | 18.3 | 76.2 | 192.1 |
| 4 | 18.4 | 64.9 | 171.1 |
| 5 | 18.4 | 63.0 | 181.1 |
Rein formal hat sich nun der Übergang zur multiple Regression bereits vollzogen. Die Frage die sich nun direkt anschließt bezieht sich auf die Bedeutung der Koeffizienten \(\beta_1, \ldots, \beta_k\). Sind diese ebenfalls als Steigungen einer Geraden zu interpretieren? Ebenso, wie lassen sich die anderen Konzepte die bereits im Rahmen der einfachen Regression behandelt wurden haben auf die multiple Regression übertragen? Zunächst aber noch ein Beispiel.
Beispiel 17.1 In Riechman u. a. (2002) wurde ein Modell erstellt um die Leistung beim 2000m Indoor-Rudern von 12 Wettkampfruderinnen anhand eines 30-Sekunden-Ruder-Sprints, der maximalen Sauerstoffaufnahme und der Ermüdung vorherzusagen. Die Autoren bestimmten das folgende Modell: \[\begin{equation*} Zeit_{\text{2000m}} = 567.29-0.163\cdot\text{Power }-14.213\cdot \dot{V}0_{2\text{max}} + 0.738\cdot\text{Fatigue} \end{equation*}\] Mit einem Standardfehler von \(\hat{\sigma} = 0.96\).
17.1 Bedeutung der Koeffizienten bei der multiplen Regression
Um die Bedeutung der Regressionskoeffzienten bei der multiple Regression besser zu verstehen ist es von Vorteil sich noch einmal die Bedeutung der Koeffizienten im einfachen Regressionsmodell zu vergegenwärtigen (siehe Abbildung 17.1).
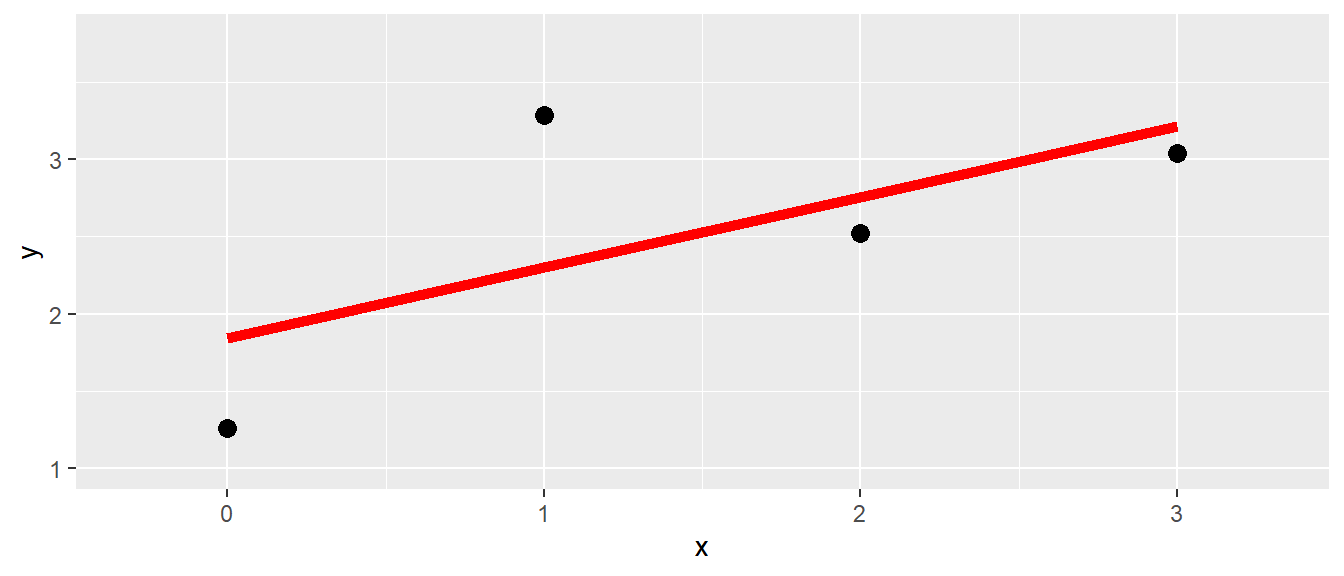
Bei der einfachen Regression wurde mittels der Methode der kleinsten Quadrate eine Regressionsgerade durch die Punktwolke der Daten gelegt. Dabei wurde die Regressionsgerade so gewählt, dass die senkrechten Abstände der beobachteten Punkte von der Regressionsgerade minimiert werden bzw. die Abstände zwischen denen auf der Gerade liegenden, vorhergesagten Werte \(\hat{y}_i\) und den beobachteten Wert \(Y_i\) (Residuen). Wird nun der Übergang von einer Prädiktorvariablen zum nächstkomplizierteren Fall mit zwei Prädiktorvariablen \(X_1\) und \(X_2\) durchgeführt, dann ist eine mögliche Darstellungsform der Daten eine Punktwolke im dreidimensionalen Raum (siehe Abbildung 17.2 (a)).
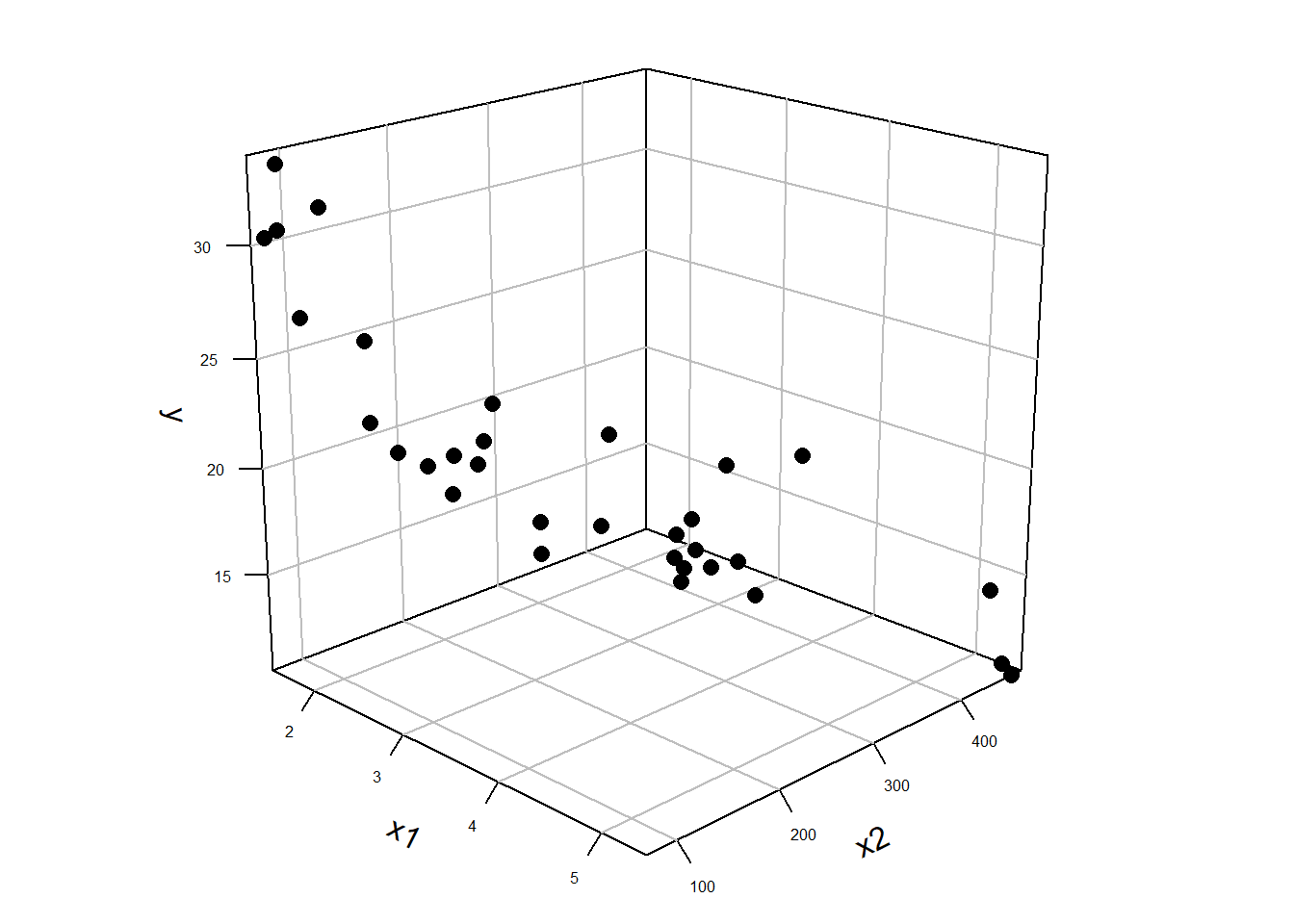
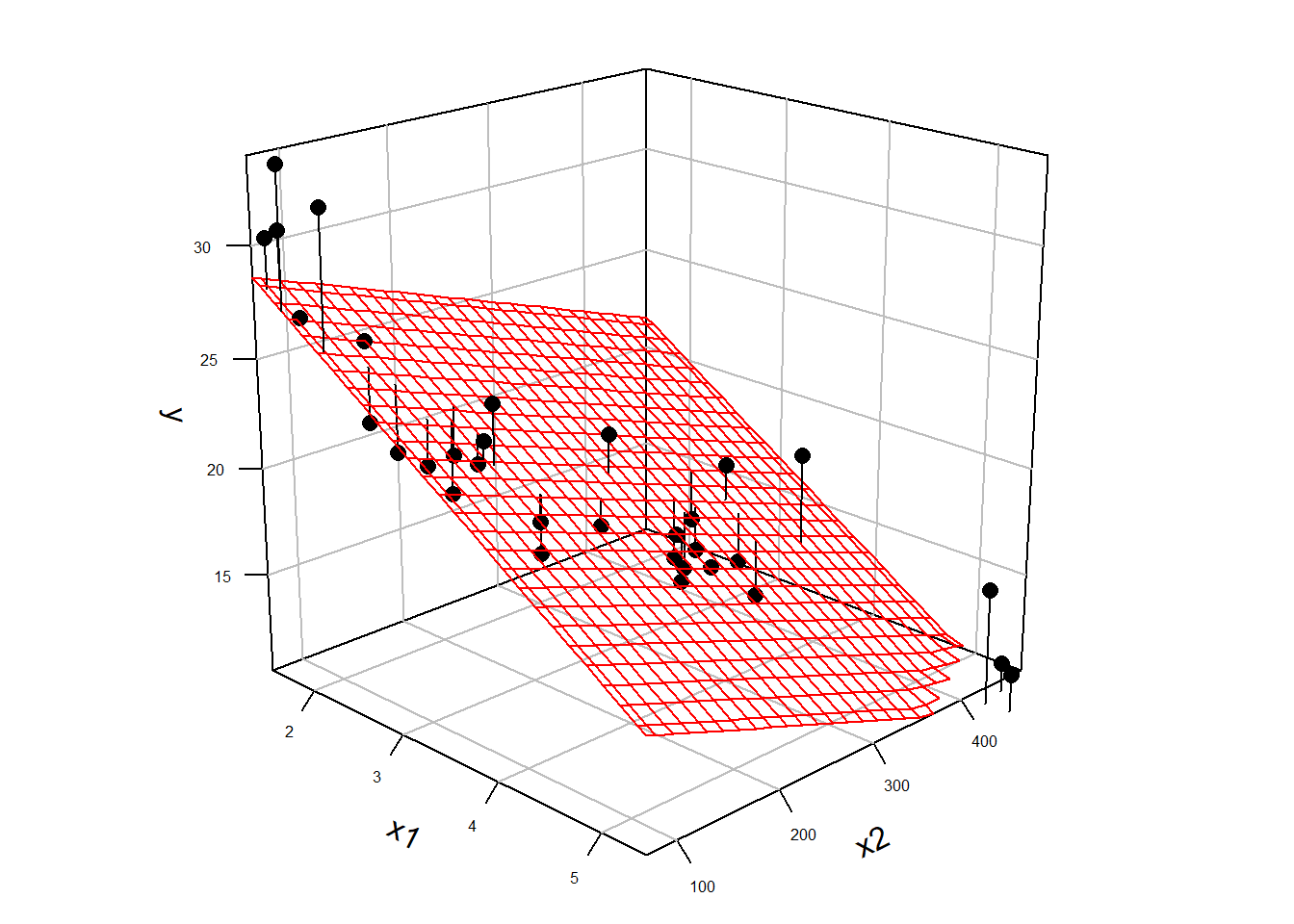
Da jetzt eine einzelne Gerade nicht mehr ausreichend ist um die Daten zu fitten, wird nun eine Ebene durch die Punktwolke gelegt (siehe Abbildung 17.2 (b)). Dieser Ansatz ermöglicht nun die gleiche Herangehensweise wie bei der einfachen linearen Regression anzuwenden. Als Zielgröße wird aus den möglichen Ebenen diejenigen Ebene gesucht, deren vorhergesagte, in der Ebene liegende, Punkte \(\hat{y}_i\) die geringsten, senkrechten Abstand zu den tatsächlich beobachteten Punkten \(y_i\) haben (wieder Residuen). Anders ausgedrückt, es wird diejenigen Ebene durch die Punktwolke gesucht deren Summe der quadrierten Residuen \(e_i = y_i - \hat{y}_i\) minimal ist. Die Definition der Residuen ist dabei genau gleich derjenigen bei der einfachen linearen Regression.
Diese Herangehensweise hat den Vorteil, dass sie zum einem die einfache lineare Regression als Spezialfall mit \(K=1\) beinhaltet und sich beliebig erweitern lässt. Lediglich mit der Einschränkung, dass bei \(K>2\) die dreidimensionale Darstellung mittels einer Grafik nicht mehr möglich ist da nicht ausreichend Dimensionen dargestellt werden können. Das Prinzip der Minimierung der Abweichungen von \(\hat{y}_i\) zu \(y\) von einer Ebene bleibt aber weiter erhalten. D.h. alle Konzepte die im Rahmen der einfachen linearen Regression erarbeitet wurden, lassen sich direkt auf die multiple lineare Regression übertragen.
Zusammenfassend:
- Die Berechnungen beim Übergang von der einfachen zur multiplen Regression bleiben alle gleich
- Die Abweichungen, die Residuen \(\hat{\epsilon_i}\) sind nun nicht mehr Abweichungen von einer Gerade sondern von einer \(K\)-dimensionalen Hyperebene. Die grundlegenden Eigenschaften der Residuen bleiben alle erhalten.
- Die Modellannahmen bleiben alle gleich: Unabhängige \(y_i\) und \(\epsilon_i \sim \mathcal{N}(0,\sigma^2)\) iid
- Inferenz für die Koeffizienten mittels \(t_k = \frac{\hat{\beta}_k}{s_k} \sim t(N-K-1)\) bleiben erhalten und übertragen sich auf die Konfidenzintervalle
- Alle Konzepte für die Vorhersage bleiben erhalten
- Modelldiagnosetools bleiben ebenfalls alle erhalten
Als nächster Schritt soll nun die Interpretation der Modellkoeffizienten im multiplen Regressionsmodell näher betrachtet werden. Dazu wird zunächst ein einfaches synthetisches Beispiel betrachtet, dass dem folgenden DGP zugrunde hat.
\[\begin{align*} y_i &= \beta_0 + \beta_1 \cdot x_{1i} + \beta_2 \cdot x_{2i} + \epsilon_i \\ \beta_0 &= 1 ,\beta_1 = 3, \beta_2 = 0.7 \\ \epsilon_i &\sim N(0,\sigma = 0.5) \end{align*}\]
Übersetzt in R code bedeutet dies, unter der Annahme, dass \(x_1\) und \(x_2\) jeweils einer Gleichverteilung mit \(U(-2,2)\) folgen. Die Annahme welcher Verteilung die beiden \(X\)-Variablen folgen, ist nicht wirklich Missionskritisch, dient die Wahl doch lediglich der einfachen Generierung von Werten.
N <- 50 # Anzahl Datenpunkte
beta_0 <- 1 # y-Achsenabschnitt
beta_1 <- 3 # 1. Steigungskoeffizient
beta_2 <- 0.7 # 2. Steigungskoeffizient
sigma <- 0.5 # Standardabweichung der Residuen
set.seed(123)
df <- tibble(
x1 = runif(N, -2, 2),
x2 = runif(N, -2, 2),
y = beta_0 + beta_1*x1 + beta_2*x2 + rnorm(N, 0, sigma)) # DGPDie Hauptlogik in dem Codeschnipsel ist die Anweisung y = beta_0 + beta_1*x1 + beta_2*x2 + rnorm(N, 0, sigma)) hier werden basierend auf den Modellparametern beta_0, beta_1, beta_2 und sigma zufällige \(Y\)-Wert erzeugt. Wenn die Prädiktorvariablen \(x_1\) und \(x_2\) gegen \(y\) jeweils in einem Streudiagramm abtragen werden, werden die folgenden Abbildungen erhalten (siehe Abbildung 17.3).

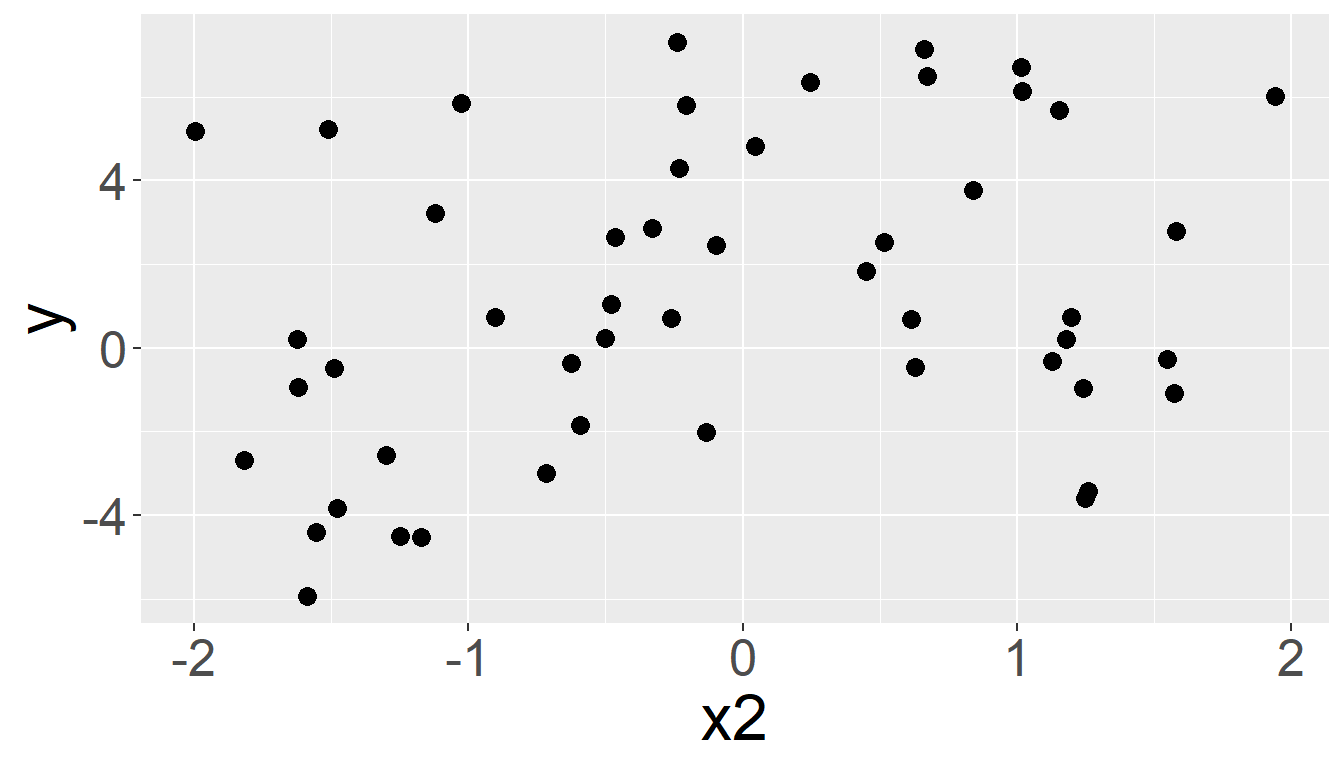
Der Zusammenhang zwischen \(x_1\) und \(y\) ist ziemlich deutlich in der Abbildung zu sehen (siehe Abbildung 17.3 (a)). Dagegen ist der Zusammenhang im Streudiagramm für \(x_2\) gegen \(y\) nicht ganz so eindeutig (siehe Abbildung 17.3 (b)). Dies ist eine Folge der (willkürlichen) Wahl der beiden Modellkoeffizienten \(\beta_1 = 3\) und \(\beta_2 = 0.7\) im Zusammenhang mit einer Varianz von \(\sigma^2 = 0.5^2\). Nun wird ein Modell mittels der lm()-Funktion in R an die Daten angepasst. Die beiden Variablen \(x_1\) und \(x_2\) gehen dem DGP folgend additiv in das Modell ein. Dies für zu der folgenden Modellformulierung für lm() y ~ x1 + x2 (Tip: Im Kapitel zur einfachen Regression ist ein kurzer Primer zur Modellformulierung).
mod <- lm(y ~ x1 + x2, df)Das gefittete Modell kann nun wie üblich mittels summary() inspiziert werden. Insbesondere können hier, wie üblich, die berechneten Modellkoeffizienten \(\beta_0, \beta_1\) und \(\beta_2\) betrachtet werden. Der Übersicht halber sind in der folgenden Tabelle (siehe Tabelle 17.2) nur die Modellparameter und deren Standardfehler angezeigt.
| \(\hat{\beta}\) | \(s_e\) | |
|---|---|---|
| (Intercept) | 1.077 | 0.066 |
| x1 | 2.965 | 0.056 |
| x2 | 0.708 | 0.060 |
| \(\hat{\sigma}\) | 0.460 |
In Tabelle 17.2 ist zu sehen, dass die anhand der Daten berechneten Koeffizienten diejenigen des DGP sehr gut reproduziert haben. Die Wert sind nicht perfekt diejenigen diejenigen die im DGP verwendet wurden, dies ist aber auf Grund der Stichprobenvariabilität nicht zu erwarten. Insgesamt sollte dieses Ergebnis jedoch beruhigend wirken, da es zeigt, dass die multiple Regression in der Lage ist die wahren Modellparameter im Rahmen der Stichprobenunsicherheit abschätzen zu können. Die einzige Neuerung im Gegensatz zur einfachen linearen Regression ist die Erweiterung um einer weitere Variablen \(X_2\) und operativ die Erweiterung in R um den Term + x2 in der Formel für lm().
Die Interpretation von \(\beta_1\) ist gleich derjenigen bei der einfachen linearen Regression allerdings mit einer kleinen Erweiterung. Zwei Objekte die sich in \(x_1\) um eine Einheit voneinander unterscheiden und den gleichen Wert in \(x_2\) haben, unterscheiden sich in der abhängigen Variablen \(y\) um den Steigungskoeffizienten \(\beta_1\). Die gleiche Interpretation mit den Rollen vertauscht trifft ebenfalls auf \(\beta_2\) zu. Zwei Objekte die sich in \(x_2\) um eine Einheit unterscheiden und den gleichen Wert für \(x_1\) haben unterscheiden sich in \(y\) um \(\beta_2\).
Im nächsten Schritt soll nun betrachtet werden, wie die Koeffizienten zustandekommen und wie die Koeffizienten zu interpretieren sind.
17.2 Interpretation der Modellkoeffizienten
Die Interpretation von \(\beta_0\) ist vollkommen identisch mit derjenigen bei der einfachen linearen Regression. Bei der einfachen linearen Regression bedeutete der Koeffizient \(\beta_0\) derjenige Wert, den das Modell annimmt, der vorhergesagte Wert \(\hat{Y}\), wenn die Prädiktorvariable \(X\) den Wert \(0\) annimmt. Graphisch ist dies der \(y\)-Achsenabschnitt. Bei der multiplen Regression bleibt diese Interpretation erhalten und \(\beta_0\) ist nun der Wert \(\hat{Y}\) wenn alle Prädiktorvariablen den Wert \(0\) annehmen. Graphisch ist dies der Schnittpunkt der Modellebene mit der \(y\)-Achse, also ebenfalls der \(y\)-Achsenabschnitt (siehe Abbildung 17.2 (b)).
Die Interpretation der Modellkoeffizienten \(\beta_1, \beta_2, \ldots, \beta_K\) bleibt zunächst auch gleich derjenigen aus der einfachen Regression. Der Koeffizient \(\beta_j, (j\neq0)\) gibt den Unterschied zwischen zwei Objekten an die sich um eine Einheit bezüglich der Variablen \(X_j\) unterscheiden. Was dabei aber etwas unklar bleibt, ist wie sich die Werte der anderen Prädiktorvariablen verhalten und welchen Einfluss diese auf diese Aussage haben?
Um diesen Zusammenhang besser zu verstehen ist zunächst eine kleine Detour notwendig. Zunächst wird eine einfache lineare Regression der beiden Prädiktorvariablen berechnet. Die Variable \(X_1\) wird durch \(X_2\) modelliert. D.h. es wird der Teil der Varianz von \(X_1\) der durch einen linearen Zusammenhang mit \(X_2\) erklärt werden. Dies führt zu folgendem Modell:
\[\begin{equation*} x_{1i} = \beta_0 + \beta_1 x_{2i} + \epsilon_i \end{equation*}\]
Anhand dieses Modells kann nun die Frage gestellt werden: Wenn \(X_2\) bekannt ist, wie viel Information wird dadurch über \(X_1\) erhalten werden? In dem Fall, dass ein perfekter linearer Zusammenhang zwischen \(X_1\) und \(X_2\) besteht dann wäre die Information von \(X_2\) über \(X_1\) ebenfalls perfekt. Für einen gegeben Wert von \(X_2\) hat, könnte der entsprechende Wert für \(X_1\) berechnet werden. Entsprechend umso schwächer der lineare Zusammenhang zwischen \(X_1\) und \(X_2\) ist, umso weniger Information besitzt \(X_2\) über \(X_1\).
Nun können aber mit Hilfe des Regressionsmodell von \(X_1\) gegen \(X_2\) die Residuen \(e_i\) berechnet werden. Aus Sicht der Information von \(X_2\) über \(X_1\), können diese interpretieren werden. Die Residuen \(e_i\) beziffern genau denjenigen Teil der Varianz von \(X_1\) der nicht mit Hilfe des Regressionsmodells von \(X_1\) gegen \(X_2\) erklärt werden kann. D.h. die Residuen \(e_i\) repräsentieren aus dieser Sichtweise die Varianz von \(X_1\) die um denjenigen Anteil von \(X_2\) bereinigt wurde. Die Residuen \(e_i\) bleiben sozusagen übrig wenn die Information von \(X_2\) aus \(X_1\) herausgenommen wird.
\[\begin{equation} e_i = x_{1i} - \beta_0 - \beta_1 x_{2i} \label{eq-mlm-basics-coef-01} \end{equation}\]
Nochmal, die Residuen \(e_i\) stellen denjenigen Teil der Varianz von \(X_1\) dar, der sich nicht durch \(X_2\) vorhersagen lässt. Eben derjenige Teil der Varianz von \(X_1\) der um den Teil von \(X_2\) bereinigt wurde. Die Residuen \(e_i\) aus Formel \(\eqref{eq-mlm-basics-coef-01}\) werden nun als eine neue Prädiktorvariablen \(x_{1i}^*\) verwendet. Formal:
\[\begin{equation*} x_{1i^*} = e_i \end{equation*}\]
Im nächsten Schritt wird nun diese neue Prädiktorvariable \(x_1^*\) verwendet um eine einfache lineare Regression von \(Y\) gegen \(x_1^*\) durchzuführen.
\[\begin{equation*} y_i = \beta_0 + \beta_1 x_{1i}^* \end{equation*}\]
In R können diese Schritte entsprechend mit lm() durchgeführt werden. Zunächst die Regression von \(X_1\) gegen \(X_2\):
mod_x1_star<- lm(x1 ~ x2, df)Das Modell mod_x1_star beinhaltet das Modell von \(X_1\) gegen \(X_2\). Im nächsten Schritt nun die Berechnung der Residuen \(e_i\).
x1_star <- resid(mod_x1_star)Diese sind jetzt einer neuen Variable x1_star zugewiesen worden. Diese Variable wird nun verwendet um eine Regression gegen \(Y\) zu rechnen.
mod_y_x1_star <- lm(y ~ x1_star, df)Das Modell ist nun mod_y_x1_star zugewiesen. Bei Betrachtung der Modellkoeffizienten werden die folgenden Wert erhalten (siehe Tabelle 17.3):
| \(\hat{\beta}\) | \(s_e\) | |
|---|---|---|
| (Intercept) | 1.250 | 0.164 |
| x1_star | 2.965 | 0.141 |
Der Steigungskoeffizient \(\beta_1\) hat genau den gleichen Wert wie in dem Modell aus der multiplen linear Regression mit beiden Variablen (siehe Tabelle 17.2).
Der Ansatz funktioniert genau gleich wenn anstatt \(x_{1i}^*\) wenn \(x_{2i}^*\) Berechnet wird indem eine einfache linear Regression von \(X_2\) gegen \(X_1\) berechnet wird und deren Residuen verwendet werden um \(Y\) zu modellieren.
mod_x2_star <- lm(x2 ~ x1, df)
x2_star <- resid(mod_x2_star)
mod_y_x2_star <- lm(y ~ x2_star, df)
coef(mod_y_x2_star)[2] x2_star
0.7081505 Wieder ist der Wert für den Steigungskoeffizienten \(\beta_2\) aus dem Modell der Gleiche wie bei dem multiplen Regressionmodell mit beiden Variablen.
Das gleiche Prinzip greift auch für mehr als zwei Prädiktorvariablen. Der einzige Unterschied ist, dass in diesem Fall nicht mehr einer Regression der Variable \(X_i\) gegen eine andere \(X_j\) Prädiktorvariable berechnet wird, sondern es wird eine multiple Regression von \(X_i\) gegen alle anderen Prädiktorvariablen \(X_j, j = 1, i-1,i+1,K\) berechnet. Die Residuen aus diesem Modell können dann wieder für eine einfache Regression gegen \(Y\) verwendet werden und der Steigungskoeffizient ist wieder gleich demjenigen der im multiplen Regressionsmodell berechnet wird.
Insgesamt folgt daraus die folgende Interpretation der Steigungskoeffizienten \(\beta_i\) im multiplen Regressionsmodell:
Der Steigungskoeffizient \(\beta_i\) drückt die Information der Variable \(X_i\) aus, wenn der gemeinsame Anteil von \(X_i\) mit allen anderen Prädiktorvariablen \(X_j, j \neq i\) rausgerechnet, bereinigt, wurde. Anders ausgedrückt: Welche zusätzliche Information wird erhalten , wenn die Variable \(X_i\) in das Modell integriert wird, wenn schon alle anderen Variablen \(X_j, j \neq i\) im Modell enthalten sind. D.h., das multiple Regressionsmodell kontrolliert automatisch immer den Einfluss der anderen \(K-1\) Variablen bei der Betrachtung der Variablen \(x_i\). Nochmal als Liste:
- \(\hat{\beta}_1\): Wenn \(X_2\) bekannt ist, welche zusätzlichen Informationen wird durch \(X_1\) über \(Y\) erhalten.
- \(\hat{\beta}_2\): Wenn \(X_1\) bekannt ist, welche zusätzlichen Informationen wird durch \(X_2\) über \(Y\) erhalten.
Bezogen auf die Werte der Steigungskoeffzienten \(\beta_i\) ist die Bedeutung immer noch wie oben, wenn sich zwei Objekte auf der Variablen \(X_i\) um eine Einheit voneinander unterscheiden und alle anderen Variablen den gleichen Wert haben, dann unterscheiden sich die erwarteten (vorhergesagten) Werte \(\hat{y}_i\) laut des Modells um \(\beta_i\).
Die Eigenschaft, dass die anderen Variablen \(X_j\) konstant gehalten werden ist dabei auch das Problem wenn ein einfaches Streudiagramm \(Y_i\) gegen \(X_i\) bei einer multiplen linearen Regression wie in Abbildung 17.3 erstellt wird. In Abbildung 17.3 (a) kann der Einfluss von \(X_1\) gut identifiziert, da der Steigungskoeffizient \(\beta_1\) im Verhältnis zu \(\sigma\) recht groß ist. Im Falle von Abbildung 17.3 (b) ist dies nicht der Fall. Ein Möglichkeit trotzdem mit Hilfe von einfachen Streudiagrammen den isolierten Zusammenhang der Prädiktorvariablen \(X_i\) auf die abhängige \(Y_i\) zu untersuchen bieten sogenannte added-variable plots.
17.2.1 Added-variable plots
Die Idee hinter den sogenannten added-variable plots basiert auf der gleichen Herangehensweise wie eben in Bezug der Berechnung einer Variable \(X_{i}^*\) mittels der Residuen \(e_i\). Neben der Bereinigung von \(X_1\) aus \(X_2\), die eben bereits verwendet wurde, wird zusätzlich auch noch der Einfluss von \(X_1\) aus \(Y\) herausgerechnet. Dazu wird wieder eine einfache lineare Regression von \(Y\) gegen \(X_1\) berechnet und die resultierenden Residuen werden verwendet. Die beiden resultierenden Variablen werden dann in einem Streudiagramm dargestellt. In R kann ein added-varaible plot mittels des folgenden Ansatzes erzeugt werden (siehe Abbildung 17.4).
y_star <- resid(lm(y ~ x1, df)) # Bereinigugn von y um x1
x2_star <- resid(lm(x2 ~ x1, df)) # Bereinigung von x2 um x1
ggplot(tibble(x2_star, y_star),
aes(x2_star,y_star)) +
geom_point() +
labs(x = 'x2 | x1', y = 'y | x1')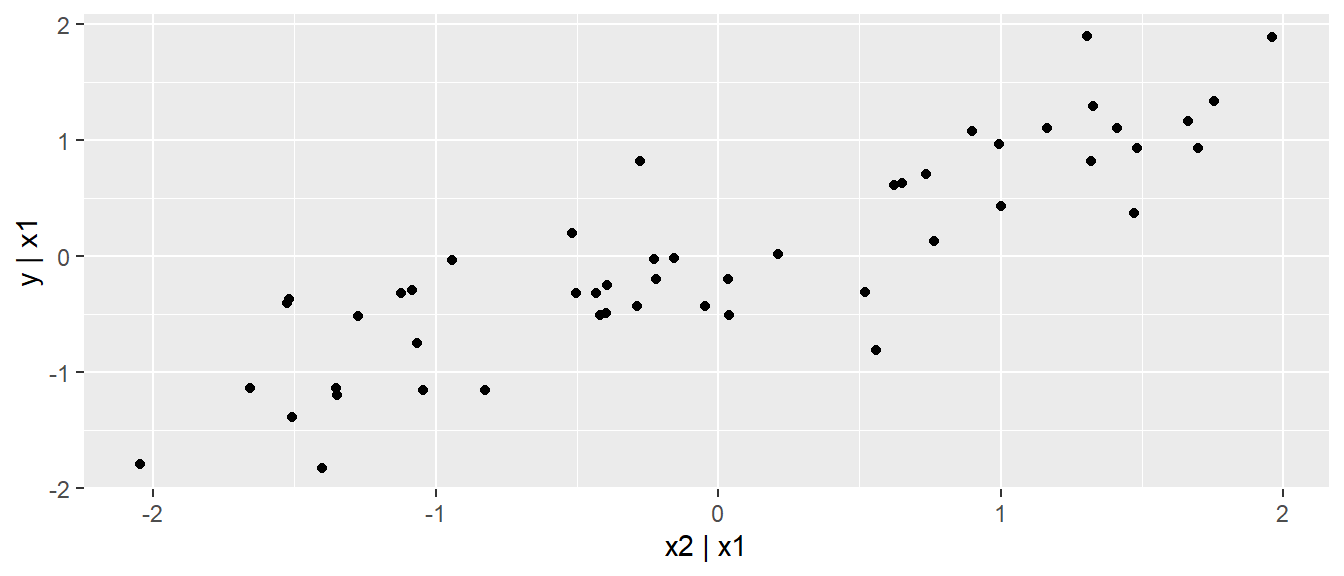
Der Zusammenhang zwischen \(X_2\) und \(Y\) ist nun viel deutlicher zu sein, als dies in Abbildung 17.3 (b) der Fall war. Im Paket car gibt es eine Funktion avPlots() mit der added-variable plots auch direkt erstellt werden können.
car::avPlots(mod)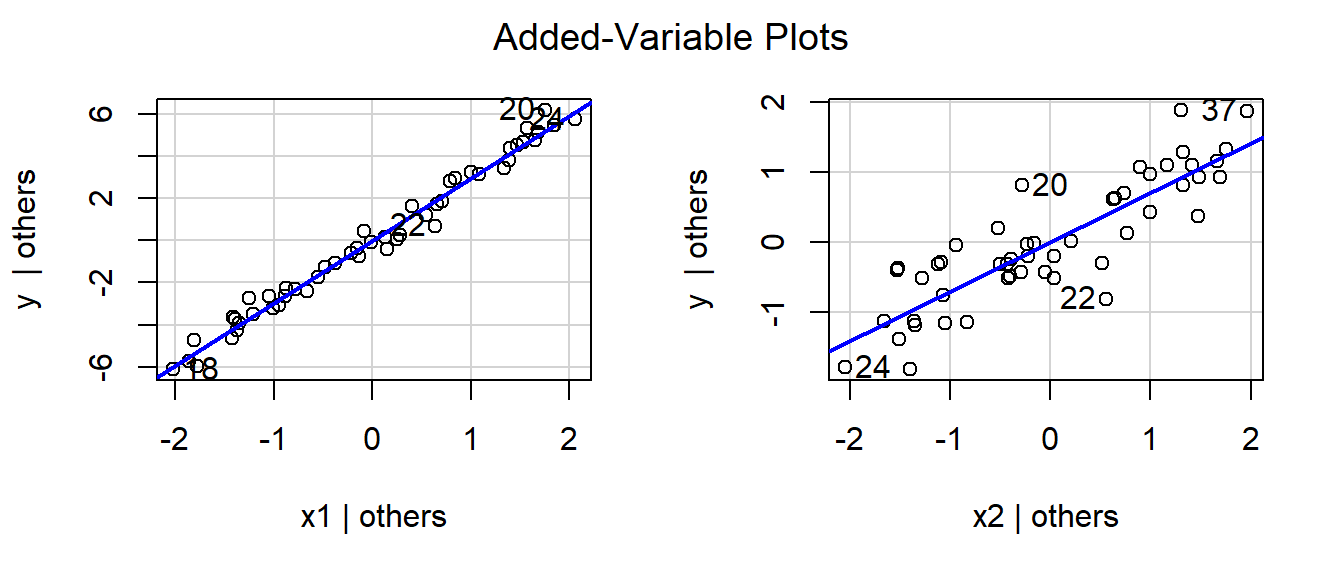
Wenn eine multiple Regression mit mehr als zwei Prädiktorvariablen gerechnet wird, dann werden im added-variable plot jeweils alle \(K-1\) Variablen aus \(x_i\) und \(y\) herausgerechnet. D.h. \(Y\) und \(X_i\) werden um den Einfluss aller, verbleibenden \(X_j, j \neq i\) bereinigt. Die Darstellung von added-variable plots ist daher im Zusammenhang einer multiplen Regressionsanalyse immer von Vorteil um den Einfluss einzelner Variablen auf die abhängige Variable zu beurteilen.
Da ein Steigungskoeffizientt \(\beta_i\) immer den Beitrag der Information von \(X_i\) über denjenigen der anderen Prädiktorvariablen hinaus bestimmt, stellt sich die Frage was passiert wenn im Modell eine oder mehrere Prädiktorvariablen weggelassen werden.
17.2.2 Was passiert wenn eine Prädiktorvariable weggelassen wird?
In Tabelle 17.4 sind noch mal die Koeffizienten aus dem Beispiel abgebildet.
| \(\hat{\beta}\) | \(s_e\) | |
|---|---|---|
| (Intercept) | 1.077 | 0.066 |
| x1 | 2.965 | 0.056 |
| x2 | 0.708 | 0.060 |
Was passiert nun, wenn anstatt einer multiplen Regression mit beiden Prädiktorvariablen zwei Einzelmodelle als einfache lineare Regression gefittet werden. Die Modell enthalten dabei jeweils mit eine der Prädiktorvariablen? Bleiben die Werte der Koeffizienten gleich derjenigen im multiplen Regressionsmodell? Dazu wird erst einmal das Modell mit nur der Prädiktorvariablen \(X_1\) berechnet:
coef(lm(y ~ x1, df))(Intercept) x1
1.007466 3.017589 Im Vergleich zum multiplen Regressionsmodell (siehe Tabelle 17.4) hat sich der Modellkoeffizient verändert. Die Größe des Werts ist zwar in einem ähnlichen Bereich, die Werte sind aber nicht genau gleich. Das Gleiche nun für \(X_2\):
coef(lm(y ~ x2, df))(Intercept) x2
1.3377771 0.9555316 Wieder ist der Wert des Modellskoeffizient anders als derjenige im multiplen Regressionsmodell (siehe Tabelle 17.4). Wieder ist die Größenordnung des Wertes aber ähnlich. Aus Sicht der vorgehenden Ausführungen betrachtet, deutet die Veränderung der Werte darauf hin, dass die Information die die Prädiktorvariablen über \(Y\) aussagen sich ändert wenn die jeweils andere Variable im Modell enthalten ist.
Wird nochmal die der DGP der Daten betrachtet, könnte eingewendet, dass in diesem Beispiel, per Konstruktion des DGPs \(X_1\) und \(X_2\) eigentlich unabhängig voneinander sollten. Als die die Daten generiert wurden, wurden jeweils zwei unabhängige Zufallszahlenmengen erstellt. Eine Antwort auf dieses Problem liefert eine kurze Betrachtung der Korrelation zwischen den beiden Variablen.
round(cor(df),3) x1 x2 y
x1 1.000 0.078 0.969
x2 0.078 1.000 0.289
y 0.969 0.289 1.000Es ist zu sehen, dass \(x_1\) und \(x_2\) miteinander korrelieren, zwar nur leicht aber die Korrelation ist nicht exakt \(=0\). D.h. \(x_1\) enthält rein durch Zufall etwas Informationen über \(x_2\). Dementsprechend ändern sich die Beiträge der Variablen zu \(y\) in Abhängigkeit davon ob die jeweils andere Variable ebenfalls im Modell enthalten ist oder eben nicht. Die Änderungen sind dabei wie oben zu sehen war nur sehr gering.
17.3 Multikollinearität
Sei nun ein anderer Datensatz betrachtet (Beispiel aus Kutner u. a. 2005). Im Rahmen einer Untersuchung sind Körperfettmessungen durchgeführt an \(20\) Personen durchgeführt worden. Neben einer Gesamtkörpermessung wurde auch der Körperfettanteil am Oberarm, Unterarm und am Oberschenkel bestimmt. In Tabelle 17.5 ist ein Ausschnitt der Daten abgebildet.
| Oberarm | Unterarm | Oberschenkel | Gesamt |
|---|---|---|---|
| 19.5 | 43.1 | 29.1 | 11.9 |
| 24.7 | 49.8 | 28.2 | 22.8 |
| 30.7 | 51.9 | 37.0 | 18.7 |
| 29.8 | 54.3 | 31.1 | 20.1 |
| 19.1 | 42.2 | 30.9 | 12.9 |
| 25.6 | 53.9 | 23.7 | 21.7 |
Als Modell sollen der Gesamtkörperfettanteil mit Hilfe der drei verschiedenen Messungen bestimmt werden.
\[\begin{equation} Y_{\text{Körperfettanteil}} = \beta_0 + \beta_1 \cdot X_{\text{Oberarm}} + \beta_2 \cdot X_{\text{Unterarm}} + \beta_3 \cdot X_{\text{Oberschenkel}} + \epsilon \end{equation}\]
Um die Daten besser zu verstehen wird zunächst betrachtet, wie stark die Werte miteinander korrelieren. Dazu wird die Funktion ggpairs() aus dem GGally Paket. Diese ermöglicht mit wenig Aufwand eine übersichtliche Darstellung der Korrelation eines tibbles (siehe Abbildung 17.5).
GGally::ggpairs(bodyfat) 
Wie bei Körperfettwerten nicht anders zu erwarten, korrelieren die Prädiktorvariablen relativ stark miteinander. Die Korrelation zwischen den Oberschenkeldaten und den Oberarmdaten in dieser Stichprobe ist sogar \(>0.9\). Die Frage ist nun, wie sich diese Korrelation auf den Modellfit auswirkt, wenn nur Teilmengen der Prädiktorvariablen zur Anpassung verwenden werden. Insgesamt können vier verschiedene Modelle verwendet werden. Ein Modell mit allen Prädiktorvariablen und drei weitere Modelle bei denen wir jeweils eine der Prädiktorvariablen weglassen. In R:
# Alle drei Prädiktoren
mod_full <- lm(body_fat ~ triceps + thigh + midarm, bodyfat)
# ohne Arm
mod_wo_midarm <- lm(body_fat ~ triceps + thigh, bodyfat)
# Ohne Oberschenkel
mod_wo_thigh <- lm(body_fat ~ triceps + midarm, bodyfat)
# Ohne Triceps
mod_wo_triceps <- lm(body_fat ~ thigh + midarm, bodyfat)In Tabelle 17.6 sind nur die Steigungskoeffizienten für die vier verschiedenen Modell abgebildet.
| Oberarm | Oberschenkel | Unterarm | |
|---|---|---|---|
| Alle | 4.33 | -2.86 | -2.19 |
| ohne Unterarm | 0.22 | 0.66 | |
| ohne Oberschenkel | 1.00 | -0.43 | |
| ohne Oberarm | 0.85 | 0.10 |
Es ist zu beobachten, dass für diese Daten die Werte der Modellkoeffizienten sich sehr stark ändern in Abhängigkeit von welche Variablen in dem Modell enthalten sind. Beispielsweise änder der Koeffizient für den Oberschenkel nicht nur seine Größe sondern auch sein Vorzeichen, je nachdem ob der Ober- oder der Unterarm oder beide im Modell enthalten sind. D.h. durch die Korrelation der Prädiktorvariablen untereinander kommt es dazu, dass die Modellkoeffizienten sehr stark schwanken in Abhängigkeit von der Variablenkombination. Wird dies wieder aus der Sicht der Information betrachtet ist dieser Effekt eigentlich auch zu erwarten. Die Interpretation der Modellkoeffizienten bei der multiplen Regression war oben hergeleitet als, wie viel Information die neue Variablen liefert nachdem die anderen Variablen schon im Modell berücksichtigt wurden. Wenn die Variablen nun sehr stark miteinander korrelieren, dann bringt eine neue Variable wenige neue Information in das Modell über diejenige Information die schon durch die anderen Variablen repräsentiert wird. D.h. bei der multiplen Regression ist die Betrachtung der Beziehung der Prädiktorvariablen miteinander wichtig bei der Beurteilung des Modells. Dieses Konzept ist so wichtig, dass es einen eigenen Namen bekommt. Wenn mehrere Variablen in einem Modell miteinander korrelieren, dann wird dies als Multikollinearität bezeichnet.
Definition 17.1 (Multikollinearität) Wenn in einem Modell Prädiktorvariablen miteinander korrelieren, dann wird dies als Multikollinearität bezeichnet.
Multikollinearität hat verschiedene Einflüsse auf das Modell die sich vor allem hinsichtlich der Stabilität der Koeffizienten auswirken, wenn Prädiktorvariablen aus dem Modell herausgenommen werden bzw. dazugenommen werden. Dazu beeinflusst Multikollinearität auch die Größe der Standardfehler der geschätzten Koeffizienten \(\hat{\beta}_j\).
Multikollinearität hat unter anderem die folgenden Effekte:
- Große Änderungen in den Koeffizienten wenn Prädiktoren ausgelassen/eingefügt werden
- Koeffizienten haben eine andere Richtung als erwartet
- Hohe (einfache) Korrelationen zwischen Prädiktoren
- Breite Konfidenzintervalle für “wichtige” Prädiktoren \(b_j\)
Es lässt sich zeigen, dass die Varianz der geschätzten Modellkoefizienten \(b_j\) die folgende Form hat (siehe Formel \(\eqref{eq-mlm-basics-varb_j}\):
\[\begin{equation} \widehat{\text{Var}}(b_j) = \frac{\hat{\sigma}^2}{(n-1)s_j^2}\frac{1}{1-R_j^2} \label{eq-mlm-basics-varb_j} \end{equation}\]
Der Term \(R_j^2\) wird als multipler Korrelationskoeffizient bezeichnet und beruht auf dem Determinationskoeffizienten der Prädiktorvariablen \(X_i, i\neq j\) auf die Prädiktorvariable \(X_j\). D.h. es wird ein Regressionsmodell gerechnet, bei dem die Prädiktorvariable \(X_j\) als abhängige Variable verwendet wird und mittels der anderen \(p-1\) Prädiktorvariablen modelliert wird.
Der zweiter Term in Formel \(\eqref{eq-mlm-basics-varb_j}\) \(\frac{1}{1-R_j^2}\) wird als Variance Inflation Factor (VIF) bezeichnet. Wie der Name bereits andeutet, kommt es durch die Korrelation der Prädiktorvariablen untereinander es zu einer Inflation der Varianzen. D.h. die Standardfehler, die Wurzeln der jeweiligen Varianzen, der Modellparameter werden vergrößert was dazu führen kann, dass die Modellkoeffizienten keine statistische Signifikanz aufweisen obwohl ein klarer Zusammenhang zwischen der Prädiktorvariablen und der abhängigen Variablen besteht. Anhand \(\eqref{eq-mlm-basics-varb_j}\) ist zu erkennen, dass wenn der Determinantionskoeffizient, also die Korrelation der Prädiktorvariablen größer Wert, der zweite Term ebenfalls an Größe zunimmt und dementsprechend die Varianz sich vergrößert.
Der VIF bietet daher eine einfache Möglichkeit, zumindest heuristisch, das gefittete Regressionsmodell auf Multikollinearitäten zu überprüfen. Der VIF wird für jede Prädiktorvariable bestimmt. Bei der Interpretatation der VIF gibt es keinen magischen Wert der für Probleme spricht. Im Allgemeinen werden die VIFs niemals komplett null sein. Bei der Beurteilung von Problemen auf Grund von Multikollinearität wird üblicherweise der größte VIF Wert im Modell betrachtet.
Wenn VIF > 10 ist, dann deutet dies auf hohe Multikollinearität hin.
Manchmal wird in der Literatur auch die sogenannte Tolerance = \(\frac{1}{VIF}\), der Inverse Wert des VIF betrachtet.
\[\begin{equation*} \text{VIF}_j = \frac{1}{1-R_j^2} \end{equation*}\]
Hinsichtlich des Einflusses bzw. des Umgangs bei Multikollinearität muss unterschieden werden, welches Ziel die Modellierung verfolgt. Das Problem das durch die Multikollinearität entsteht ist, basiert darauf das das Modell nicht eindeutig zuordnen kann, welche der miteinander korrelierten Variable für die beobachteten Veränderungen in der abhängigen Variablen \(Y\) zuständig ist. Multikollinearität vermindert dabei nicht die Fähigkeit des Modells Mittelwerte \(E[y|x]\) vorherzusagen oder einen guten Modellfit zu erhalten. Allerdings verkompliziert sich die Interpretation der Modellkoeffizienten \(\hat{beta}_j\). Dadurch das die Prädiktorvariablen miteinander korrelieren, kann es beispielsweise gar nicht praktisch möglich sein die Variablen einzeln zu variieren, wodurch die Interpretation des Koeffizienten \(b_j\) als die Veränderung von \(y\) bei Veränderung von \(x_j\) um eine Einheit problematisch wird. Weiterhin, dadurch das durch die Multikollinearität die Varianzen der Modelkoeffizienten vergrößert werden, kann es zu dem Fall kommen, dass ein Modellkoeffizienten \(b_j\) statistisch nicht signifikant ist, obwohl eindeutig ein Zusammenhang zwischen \(x_j\) und \(y\) besteht. Zusätzlich, dadurch das die Modellkoeffizienten sich stark verändern können bei Veränderung des Modells ist deren Interpretation grundsätzlich problematisch.
17.3.1 Variance Inflation Factor (VIF) in R berechnen
In R kann der VIF am einfachsten über zwei Funktionen berechnet werden. Einmal über die vif()-Funktion aus dem Paket car.
car::vif(mod_full) triceps thigh midarm
708.8429 564.3434 104.6060 Eine weitere Möglichkeit besteht mittels der Funktion check_collinearity() aus dem performance Paket.
performance::check_collinearity(mod_full)check_collinearity()
| Term | VIF | VIF_CI_low | VIF_CI_high | SE_factor | Tolerance | Tolerance_CI_low | Tolerance_CI_high |
|---|---|---|---|---|---|---|---|
| triceps | 708.8429 | 383.98652 | 1309.2486 | 26.62410 | 0.0014107 | 0.0007638 | 0.0026043 |
| thigh | 564.3434 | 305.76950 | 1042.2977 | 23.75591 | 0.0017720 | 0.0009594 | 0.0032704 |
| midarm | 104.6060 | 56.91565 | 192.9714 | 10.22771 | 0.0095597 | 0.0051821 | 0.0175699 |
In Tabelle 17.7 ist zu sehen, dass check_collinearity() auch noch Konfidenzintervalle und besagten Tolerance Parameter ausgibt. In jedem Fall, ist zu sehen, dass bei Anwendung der Daumenregel \(VIF > 10\), hohe Multikollinearität in unserem Körperfettmodell zu beobachten sind. Dies erklärt somit auch die großen Veränderung in den Koeffizienten bei Hinzu- bzw. Entnahme der Prädiktorvariablen.
Beispiel 17.2 (Gehparameter bei Älteren) Die Beziehung zwischen gebrechlichen älteren Menschen und der Gehgeschwindigkeit ist entscheidend, um den Bedarf an Langzeitpflege oder erhöhter Unterstützung zu minimieren. Insbesondere ist der Zusammenhang zwischen Gehleistung, respiratorischer Funktion und dynamischem Gleichgewicht bei älteren Menschen, die auf Langzeitpflege angewiesen sind, noch nicht gut verstanden. Zu diesem Zweck wurde in Jiroumaru u. a. (2023) der Zusammenhänge zwischen Gehgeschwindigkeit, Atemmuskelkraft und dynamischem Gleichgewicht mittels multipler Regressionsanalyse untersucht.
Die Atemmuskelkraft wurde mittels des maximalen inspiratorische (PImax) und des maximalen exspiratorische Drucks (PEmax) bestimmt. Der maximale Doppelschrittlängentest (MDST) wurde als Index für das dynamische Gleichgewicht verwendet. Eine multiple Regressionsanalyse wurde durchgeführt, wobei die Gehgeschwindigkeit (normale und maximale Gehgeschwindigkeit) als abhängige Variable und PImax, PEmax sowie MDST als unabhängige Variablen verwendet wurden. Zusätzlich wurde das Geschlecht als Anpassungsvariable berücksichtigt und in den Daten als entweder \(0\) oder \(1\) kodiert. Die Daten sind im repository zum Skriptum zu finden. Eine Analyse der Daten für die abhängige Variable maximale Gehgeschwindigkeit (mws) führte zu folgendem Ergebnis:
Call:
lm(formula = mws ~ Pemax + mdst + Pimax + gender, data = jiro)
Residuals:
Min 1Q Median 3Q Max
-0.49647 -0.11938 0.02674 0.09814 0.63112
Coefficients:
Estimate Std. Error t value Pr(>|t|)
(Intercept) -0.089055 0.143775 -0.619 0.5388
Pemax 0.005391 0.002381 2.264 0.0286 *
mdst 0.810667 0.156529 5.179 5.33e-06 ***
Pimax 0.005307 0.002804 1.893 0.0650 .
gender -0.121083 0.083215 -1.455 0.1528
---
Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
Residual standard error: 0.2387 on 44 degrees of freedom
Multiple R-squared: 0.6331, Adjusted R-squared: 0.5998
F-statistic: 18.98 on 4 and 44 DF, p-value: 3.918e-09D.h. es wurde ein stastistisch signifikanter Zusammenhang der maximalen Gehgeschwindigkeit mit PEmax und MDST beobachtet. Eine Untersuchung des VIF deutete auf keine starken Multikollineariäten zwischen den Variablen hin.
car::vif(mod) Pemax mdst Pimax gender
2.137365 1.255722 1.866983 1.458773 17.3.2 Wenn Prädiktorvariablen \(X_j\) sich gegenseitig maskieren
Insgesamt sind aus der operativen Seite durch den Übergang von der einfachen zur multiplen Regression keine großen Neuerungen hinzugekommen. Allerdings müssen jetzt, wie schon bezüglich der Multikollinearität gesehen wurde, das Verhältnis der Prädiktorvariablen \(X_j\) untereinander näher betrachtet werden. Das folgenden Beispiel ist McElreath (2016) entnommen und zeigt noch einmal zu welchen unerwarteten Effekten es kommen kann, wenn die Prädiktorvariablen miteinander in Beziehung stehen. In diesem Beispiel kommt es tatsächlich zu einer Maskierung der Effekt untereinander wenn Variablen hinzugenommen bzw. weggelassen werden. Daraus resultieren ebenfalls große Veränderungen in den Modellkoeffizienten in Abhängigkeit von der Kombination der Prädiktorvariablen.
Um das Beispiel so anschaulich wie möglich zu machen, wird ein DGP mit nur zwei Prädiktorvariablen \(X_{pos}\) und \(X_{neg}\) verwendet. Die Prädiktorvariable \(X_{pos}\) sei positiv mit \(Y\) korreliert, während die Prädiktorvariable \(X_{neg}\) negativ mit \(Y\) korreliert ist. Zusätzlich seien die beiden Prädiktorvariablen Variablen positiv miteinander korreliert. Es werden \(N = 100\) Datenpunkte simuliert. Die genaue Herleitung der Werte ist im einzelnen nicht wichtig und die Werte sind wie immer bei den verwendeten Simulationen der Einfachheit halber gewählt. Zwischen \(X_{pos}\) und \(Y\) besteht eine Korrelation von \(rho_{X_{pos}y} = 0.15\), zwischen \(X_{neg}\) und \(Y\) von \(rho_{X_{neg}Y} = -0.5\) und zwischen den beiden Prädiktorvariabeln von \(rho_{XX} = 0.5\)
Sigma <- matrix(c(1,0.15, -.5, 0.15, 1, 0.5, -0.5, 0.5, 1), nr=3)
Sigma [,1] [,2] [,3]
[1,] 1.00 0.15 -0.5
[2,] 0.15 1.00 0.5
[3,] -0.50 0.50 1.0Um die gewünschte Korrelationsstruktur zwischen den Variablen kann nun die Funktion mvrnorm() aus dem Paket MASS verwendet werden. Mit mvrnorm() können Zufallszahlen generiert werden, die eine multivariaten Normalverteilung mit einer vorgegeben Kovarianzstruktur folgen.
set.seed(123)
N <- 100
df_temp <- MASS::mvrnorm(n = 100, mu = c(0,0,0), Sigma=Sigma)
colnames(df_temp) <- c('y','x_pos','x_neg')
df <- as_tibble(df_temp)In Abbildung 17.6 ist die resultierende Korrelationsmatrize der drei Variablen abgebildet.
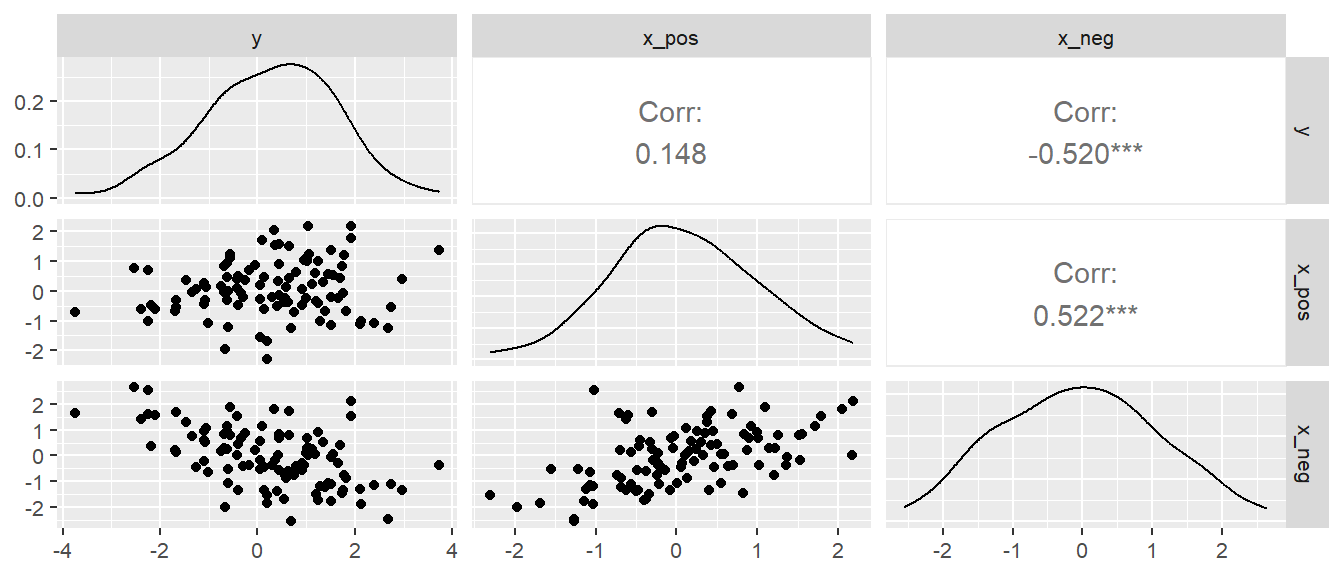
Es ist zu sehen, dass x_pos und x_neg die gewünschte Korrelation mit \(y\) aufweisen sowie ebenfalls eine positive Korrelation miteinander aufweisen. Nun werden wieder drei verschiedene Modelle angepasst. Ein Modell mit bei Variablen, eine Modell mit nur \(x_{pos}\) und ein Modell mit nur \(x_{neg}\) als Prädiktorvariablen. In Tabelle 17.8 sind die resultierenden Modellkoeffizienten für die drei Modelle dokumentiert.
| \(\hat{\beta_0} \pm s_e\) | \(\hat{\beta}_{pos} \pm s_e\) | \(\hat{\beta}_{neg} \pm s_e\) | |
|---|---|---|---|
| pos | \(-0.1\pm 0.1\) | \(0.17\pm 0.11\) | |
| neg | \(-0.04\pm 0.09\) | \(-0.57\pm 0.1\) | |
| pos + neg | \(0.03\pm 0.07\) | \(0.54\pm 0.09\) | \(-0.85\pm 0.1\) |
Es ist zu erkennen, dass die Größe der Modellkoeffizienten sehr stark davon abhängt welche Variablenkombination gefittet wird. Für das Modell mit nur dem positiven Prädiktor \(x_{pos}\) kann bei Verwendung der Daumenregeln \(\pm 2\times \text{SE}\) erkannt werden, dass der Modellkoeffizient \(b_{pos}\) statistisch nicht signifikant ist. Erst wenn beide Prädiktorvariablen in dem Modell inkludiert sind, ist der Modellkoeffizient statistisch signifikant. Im ersten Modell maskiert der Effekte der Prädiktorvariablen \(x_{neg}\), welche gar nicht im Modell enthalten ist, den Effekt von \(x_{pos}\) auf \(y\). Erst wenn beide Variablen im Modell auch enthalten sind, ist das Modell in der Lage den Effekt auch tatsächlich zu erfassen.
Zusammenfassend ist es entsprechend wichtig dass bei der Modellierung mittels einer multiplen linearen Regression theoretische Vorüberlegungen über die relevanten Variablen in die Studie mit eingehen. Ein einfaches probieren mittels In- und Exklusion von Prädiktorvariablen wird selten zum gewünschten Erfolg führen bzw. zu einem robustem Modell führen. Zumindest wenn es darum geht den Werten der Modellkoeffizienten auch inhaltliche Bedeutung zuweisen zu können.
17.4 Unter der Motorhaube von lm() die Modellmatrix
Für die weitere Arbeit mit der multiplen linearen Regression ist es von Vorteil ein etwas tiefergehendes Verständnis der Berechnungen in R bei der Verwendung von lm() zu haben. Insbesondere die Kenntnis der sogenannten Modellmatrix ist dabei von Vorteil.
Definition 17.2 (Modellmatrix) Die Modellmatrix , auch als Designmatrix oder Regressionsmatrix , ist eine Matrix welche die zur Modellierung verwendeten Daten in Form einer Matrix enthält. Jede Zeile der Modellmatrix repräsentiert eine Beobachtung, während jede Spalte einer Prädiktorvariable entspricht. Die Modellmatrix wird oft mit dem Buchstaben \(X\) bezeichnet.
In R kann eine Modellmatrix mit Hilfe der Funktion model.matrix() erzeugt werden. Am einfachsten ist die Funktion anhand eines Beispiels nach zu vollziehen. Sei der folgende einfache Beispieldatensatz gegeben:
df <- tibble(
y = c(1,3,2.5,7),
x_1 = 1:4,
x_2= c(11,11,14,13)
)Wenn nun eine lineares Modell an die Daten gefittet wird, dann würde die folgende Syntax verwendet werden lm(y ~ x_1 + x_2) entsprechend zu dem Modell \(y_i = \beta_0 + \beta_1 x_{1i}+ \beta_2 x_{2i} + \epsilon_i\). Was nun intern in lm() passiert ist, das die Berechnung auf ein mathematisches Problem abgebildet wird, das mit Hilfe von Matrizenalgebra gelöst wird. Die genaueren Schritte sind zunächst nicht weiter wichtig, sondern nur der erste Schritt die Erstellung der Modellmatrix \(X\). Die erzeugte Modellmatrix kann angezeigt werden, indem die Funktion model.matrix() auf das Modellobjekt angewendet wird.
mod <- lm(y ~ x_1 + x_2, df)
model.matrix(mod) (Intercept) x_1 x_2
1 1 1 11
2 1 2 11
3 1 3 14
4 1 4 13
attr(,"assign")
[1] 0 1 2Alternativ kann die Modellmatrix anhand der Formel und dem Datensatz erstellt werden:
model.matrix(~ x_1 + x_2, data = df) (Intercept) x_1 x_2
1 1 1 11
2 1 2 11
3 1 3 14
4 1 4 13
attr(,"assign")
[1] 0 1 2Laut der Definition, ist die Modellmatrix \(X\) die numerische Darstellung der Prädiktorvariablen mittels einer Matrix. In der zweiten Spalte sind die Werte der Variablen x_1, während in der dritten Spalte die Werte der Variablen x_2 eingetragen sind. Die Spalten entsprechen also den jeweiligen Einträgen der Prädiktorvariablen \(x_{ji}\). Die erste Spalte sticht hier etwas raus, da hier nur \(1\) eingetragen sind. Diese Spalte ist dem ersten Modellkoeffizienten \(\beta_0\) zugeordnet, also dem konstanten \(y\)-Achsenabschnitt. Dies hat den Vorteil, dass die vorhergesagten Werte durch eine einfache Matrixmultiplikation berechnet werden können (im Anhang ist dazu eine kurze Erläuterung, ist aber nicht notwendig für das weitere Verständnis).
beta_s <- coef(mod)
X <- model.matrix(~ x_1 + x_2, df)
X %*% beta_s [,1]
1 0.6296296
2 3.4629630
3 2.6851852
4 6.7222222Die Modellkoeffizienten werden bei der Berechnung der Werte \(\hat{y}_i\) immer multiplikativ mit der jeweiligen Spalte verbunden. Etwas explizierter.
\[\begin{equation*} \hat{y} = \begin{pmatrix} \hat{y}_1 \\ \hat{y}_2 \\ \hat{y}_3 \\ \hat{y}_4 \end{pmatrix} = \begin{pmatrix} 1 \\ 1 \\ 1 \\ 1 \end{pmatrix} \times \hat{\beta_0} + \begin{pmatrix} 1 \\ 2 \\ 3 \\ 4 \end{pmatrix} \times \hat{\beta_1} + \begin{pmatrix} 11 \\ 11 \\ 14 \\ 13 \end{pmatrix} \times \hat{\beta_2} = X \hat{\beta} \end{equation*}\]
Dies sind dementsprechend die gleichen Werte \(\hat{y}_i\) wie mittels der Funktion predict() berechnet werden.
predict(mod) 1 2 3 4
0.6296296 3.4629630 2.6851852 6.7222222 Wenn sich nun das Modell ändert, dann ändert sich dementsprechend auch die Modellmatrix \(X\). Zu Beispiel bei der Hinzunahme von weiteren Prädiktorvariablen verändert sich die Modellmatrix \(X\) dahingehend, dass zusätzliche Spalten an die Matrix angehängt werden. Etwas interessanter wird es, wenn im weiteren Verlauf des Skripts Interaktionseffekte und kategoriale Variablen in das Modell aufgenommen werden. Hier ist dann Kenntnis über die Modellmatrix von Vorteil um die Bedeutung der Modellkoeffizienten besser verstehen zu können.
17.5 Take-away
- Bei der multiplen Regression wird das Modell um zusätzliche Prädiktorvariablen erweitert
- Die Interpretation der Modellkoeffizienten ist bezieht sich auf den Einfluss der jeweiligen Variblen über denjenigen der anderen Variablen hinaus
- Die Korrelation der Prädiktorvariablen, die Multikollinearität, untereinander kann zu unvorhergesehenen Effekten bei den Modellkoeffizienten führen
17.6 Zum Nacharbeiten
Die folgenden Texte eignen sich gut um die Inhalte noch einmal zu vertiefen. Altman und Krzywinski (2015) diskutiert noch mal eingehend was passiert wenn Variablen miteinander korrelieren und wie sich das auf die Schätzer für die Koeffizienten auswirkt. (Kutner u. a. 2005, p.278–288) und (Fox 2011, p.325–327) sind nochmal als Zusammenfassungen zu lesen.